一篇文章入门“求解器”开发(全篇)
前言
全文约2万字,详细阅读时间约30分钟。内容为工业软件中设计仿真软件的多物理场仿真求解器研发,文章并不针对某种具体物理场(结构,声,热,光,电磁,流体),也不针对某个行业
(CAE/EDA/CFD/TCAD/CAO/CAPP)的数值求解器,而是介绍求解器开发的一些通用方法,工具,理论和设计思想。
读者对象为初步接触求解器的软件研发人员,文中提到的很多用颜色标记的内容可以作为关键字单独搜索。
需要提醒的是:原理性内容的学习最好的方法还是看经典教材,本文只是一些入门和科普性质的内容
1.求解器定义
这里的求解器主要是工业设计仿真软件中的内容,由英文Solver翻译而来,Solver是个比较通用的叫法,有些软件程序会叫做Engine(引擎),或者Kernel Program(核心程序),其实都是一个意思。它的主要目的是利用程序,求解多物理场问题。几何相关的约束求解器,运筹优化中的求解器等不在此讨论范畴
后续如果不做特殊说明,“求解器”默认指商用软件求解器
工业仿真软件一般分为三个大模块:
前处理器,求解器,后处理器
1.前处理器主要处理几何,设置业务数据以及求解器需要的数据(网格,属性,配置);
2.求解器读取前处理的数据进行仿真计算,并导出结果;
3.后处理器则对求解器的计算结果进行加工,显示相应计算结果。
在这三个模块中,求解器是核心,前后处理都是围绕求解器进行。在工业仿真软件发展历史中,有很多只做求解器,不做前后处理开发的公司。最为典型的是LS-DYNA产品,早期只聚焦于求解器开发,前后处理器都是其它公司围着转,后来从业务上考虑才自己开发前后处理器。ANSYS公司的产品ANSYS从上世纪90年代就提供了LS-DYNA的前处理功能,直到20多年后将其收购。
一般商业软件都会把求解器做成单独的可执行程序(*.exe程序),单独启动进程求解,用文件的形式和前处理器和后处理器交互,而不是集成在前处理器中。
一是单独的进程便于管理(比如License)和分布式计算;
二是解耦前处理器和求解器,方便测试,调试,集成和模块化;
三是可以方便与第三方工具交互(数值优化工具,CAD设计工具)。
这种结构从四五十年前软件设计之初一直沿用到现在,没有特殊原因无需改动。比如OpenFOAM中,每一种求解器都可以编译成单独的可以执行程序。
考虑一般情况,多物理场仿真求解方法包括数值解和解析解,或者半数值半解析解。目前大部分商业软件和主流方法还是纯数值解,主要原因在于数值解通用性,扩展性和兼容性强,但一般计算量偏大;解析解在特定场合效率和精度更高,但通用性较差。在求解器框架设计中,这两种方法都需要考虑到。计算机普及前的大型工程项目计算一般是解析解+手算数值解
从另外一个角度定义求解器,就是质量。这一点也是经常提及的,工业软件一定是高质量的,中低端的工业软件没有市场;买两套国产实际使用国外盗版不可能长久维持。
在给工业仿真软件研发打分(点击链接查看)一文,提到了软件质量评分。80分的标准如下,作为仿真软件核心的求解器也类似:

2. 求解器研发流程
求解器开发一般可以分为三个阶段:
1. 原型开发
这阶段主要完成以下任务:
1.技术选型;
确定要实现的功能,使用的开发语言,开发环境和工具。目前大部分求解器开发使用C/C++/Fortran语言
2 实现基本功能;
要能对最简单的例子进行计算,并得到正确的结果。需要做的工作:
2.1.能生成标准求解器的输入文件,比如Nastran,Ansys,HFSS,Fluent等的求解器输入文件,例子的计算结果要与这些标准求解器计算的结果做比较。
2.2.标准求解器输入文件的解析器。用来解析输入文件,作为开发求解器的输入数据。
2.3.比较标准求解器的计算结果和开发的求解器结果。
这阶段的主要目的是保证算法的正确性。开发时为了提高效率,可以借助类似Matlab软件: 用Matlab完成原型的开发,直到计算结果正确。在此基础上再将Matlab翻译成 C++/Fortran。这样在早期可以将精力集中在算法验证上,需要注意的是尽量进行模块化开发。
3. 完成求解器原型;
1. 需要开发一种标准求解器文件的解析器。
2. 需要熟练使用标准CAE软件进行仿真,熟悉求解器输入文件和计算结果
3. 开发的求解器要能正确计算经典的Benchmark例子
原型开发决定了开发的可行性,如果这阶段的目标无法完成,需要加强研发的投入。
2. 迭代开发
这阶段主要完成以下任务:
1. 完善新功能
在完成原型的基础上,添加新功能,比如支持新的单元类型,支持新的荷载边界,处理更复杂的模型等。
2. 保证计算准确性基础上,进一步提高求解器的质量
正确性:正确的模型,都能给出可靠的计算结果;
稳定性:能给出正确的反馈,保持稳定;
效率:计算速度,内存消耗。考虑异构计算和并行分布式计算。
3. 完善求解器的前处理和后处理:
有限元模型检查
网格质量检查
仿真结果分析
4. 创建更多经典的Benchmark进行测试。
小结:
迭代开发阶段的主要目的是完善求解器,建立规范化的开发流程:
1. 确定技术选型,比如线性方程组库的使用,并行计算,GPU等
2. 完善前处理和后处理
3. 建立更多经典Benchmark例子,例子的选择需要 有经验的工程师的参与
4. 确定求解器输入文件格式
5. 定期发布版本以供测试
3. 维护开发
这阶段主要完成任务有:
1. 测试实际工程的例子,处理实际工程中所碰到的问题
实际工程的模型要远比经典模型复杂,求解器需要更多的功能支持计算实际的模型。
2. 建立回归测试机制
回归测试是求解器开发中非常重要的一环,通常求解器修改后,需要验证是否对以前的功能有影响,这就需要建立回归测试机制。
开发中通常会建立很多测试用例,用一种脚本语言(Python,Perl)开发回归测试程序。每次修改代码提交前,需要运行回归测试程序,比对修改后与修改前的计算结果。如果结果相同,则认为是一次成功的代码提交,否则需要检查代码。如果不同结果是正确且符合预期,则需要修改基准测试用例。
一般我们说研发,包括研究和开发两部分,研究侧重于技术探索性质,而开发则是任务具体执行。
一个新的软件研发项目开始前,通常有两种典型情况:一是已经充分理解了项目需求,技术路线和技术方案比较成熟,可以容易的写出设计文档,并分解成具体任务供研发人员执行,工作量和节点都比较明确,这类研发主要以开发为主,就好像工厂流水线,容易执行,也容易控制进度,敏捷开发就比较适用于这种情况;第二种则相反,项目开始前,只有一个大概的需求,或者只知道对标软件,至于如何开发,使用什么技术,需要投入多少资源,什么时间节点能出什么结果,都不太清楚。很多时候求解器开发属于第二种。
对于第二类情形也有具体的研发流程,核心就是Prototype Dev,也就是原型开发。原型开发之初不要求太多设计和实现细节,而是快速开发出一个满足基本能用的原型程序。在开发原型的过程中,理清技术路线,技术选型,模块划分,工作量估算等事项,为后续的具体工作打下基础。如果原型工作之后对开发仍然毫无头绪,就需要引入经验更丰富的应用工程师和研发人员。原型开发到一定程度后,需要评估设计和功能效果,如果整体架构尚可,可以使用原有结构;如果再继续开发困难,则需要推倒重来。
推倒重来并不是坏事,越早重来,能更及早发现问题,其开发成本就越低。对于原型开发,推倒重来一两次是很正常的事。研发之初做好模块封装和重用,也能有效降低推倒重来的成本。
3.了解偏微分方程
3.1.偏微分方程
(Partial Differential Equations)
是多物理场仿真技术的起点和理论基础。偏微分方程在不同行业又叫控制方程或本构方程,笔者习惯叫“控制方程”。
从经典的热传导方程,波动方程,赫姆霍兹方程,再到拉普拉斯,泊松方程,以及纳维斯托克方程,麦克斯韦方程,以及薛定谔方程。几乎每一个方程都是一种物理场或者某一类行业里的控制方程。这些经典的偏微分方程可能相互有联系,比如拉普拉斯和泊松方程差别在于一个源项,赫姆霍兹方程是麦克斯韦方程的一种特殊形式,在这些基础方程上,通过简化,扩展又会衍生成出各种特殊的方程。
根据笔者的研发经历,将研发相关知识分为四类,也包括求解器:
第一类是理论基础。比如各种数值理论,控制方程,数学公式等等,这类知识其实不需要过于深究,原因在于这类知识类似于万有引力理论,它反映了万事万物的一些规律特征,其实很难理解,记住就好。这一块知识是科学家,数学家的工作。
第二类是推导计算。在第一类知识的基础上,通过公式推导,理论验证,将其变成可编程实现的算法和代码。这一块理论相对成熟,研发都有迹可循;但需要一定的技术积累,有相当的技术门槛,在某些前沿领域还是有不确定的因素,查阅论文,期刊是常有的事,对应于软件研发中的原型开发技术,CAE软件研发的一些思考(5)--系统的开发求解器一文中有过介绍。这一块需要对业务有相当的知识积累,也是对数学和业务依赖最多的部分。
第三类是工程应用。工程应用是在第二类知识的基础上的拓展,这类知识就要求在研发中着重需要解决实际工程问题。实际工程问题的特点是模型规模大复杂,各种参数偏离标准模型假设,特征高度非线性,有各种不合理设计,存在性价比的问题,系统工程特征突出。这类知识通常都是现成的技术方案,但是内容多,知识繁杂,交错各种非技术因素,要找到一个适合业务的技术方案也不是简单的事情。
第四类是软件开发。这个包括了基本的语言开发,需求分析,架构设计,流程管理,技术选型,系统集成等一系列和软件工程相关的知识。通常做求解器开发的朋友接触较少。但这块对于一款软件产品却又至关重要。
偏微分方程理论属于第一类理论基础,对于研发来说,可能并不需要我们研究的太深,但是理解偏微分方程的特点却能很好的帮助求解器开发:目前大部分偏微分方程都为二阶,即最高偏导两次,在构造形函数时,二阶多项式性价比往往最好;在多物理场耦合仿真中,往往首先需要明确不同物理场构成的偏微分方程组,偏微分方程组的强耦合求解仍然是世界难题,实际工程中一般使用弱耦合求解。COMSOL软件是目前对偏微分方程求解支持比较好的工具,可以支持用户自定义的偏微分方程和方程组,抛开工业应用和精度不谈,是名副其实的多物理场仿真软件。
3.2.偏微分方程要点
Partial differential equation(简称PDE),即使不理解偏微分方程,对于求解器开发问题也不大。大多数情况我们只要对其基本要点有所了解即可。这里稍微展开介绍偏微分方程的一些要点:
1. 二阶PDE三种类型
曲线,椭圆,抛物线
这个分类主要是根据方程的系数关系来确定,不同类型的PDE在数值计算上对参数的选择也有影响。
2. PDE通解和特解
没有初始条件的偏微分方程一般会有无数多个解,也就是满足多个函数表达的通解。求偏微分方程的定解问题可以先求出它的通解,然后再用定解条件确定出函数。这里的通解和定解都是解析解,非数值解。但是一般来说,在实际中通解是不容易求出的,用定解条件确定函数更是比较困难的。
3.强形式和弱形式
强形式是指需要完全满足物理模型的条件,这就会导致极难找到满足偏微分方程强形式的解析解的。而将微分方程转化为弱形式,比如求导转成积分,就是弱化对方程解的要求(比如求导要求函数连续,而积分则不用),而降低了方程求解的条件,使解能够以离散的形式存在。强形式和弱形式的概念在使用COMSOL中求解自定义PDE会碰到。
4.边界条件和荷载
在实际物理场分析中,正确的边界条件和荷载,能确定解的唯一性,相反,错误的边界荷载会导致数值解最后求解失败,比如迭代求解结果发散,或矩阵奇异等。
在数值解计算方法上,通常需要离散对象或求解区域。
根据是否需要划分拓扑网格,常用的方法又可以分为有网格和无网格方法:
有网格方法包括:
FEM,Finite Element Mehtod
FVM,Finite Volume Mehtod
FDM,Finite differential Method
MOM,Method of Moment
BEM,Boundary Element Method
DEM,Discrete Element Method
在网格方法中,MOM/BEM可以认为是半数值半解析解
无网格方法包括:
HPS
LBM,Lattice Boltzmann Method
Spectrum Method
FDTD
具体参加:
一篇文章入门无网格方法(1)(点击链接查看)
1.有限元
有限元是目前工业软件仿真领域最常用的数值方法,没有之一。其特点是对求解对象划分网格,对每个网格单元构建刚度矩阵,然后将所有网格单刚矩阵组装整体刚度矩阵,将各种边界,激励,荷载加入其中,最后形成一个线性方程组,其中系数矩阵稀疏,有些对称,有些不对称。显式动力学没有线性方程组。该方法优点是适应性好,通用性强,没有太多前提要求。一篇文章入门多物理场有限元(全篇)(点击链接查看)
2.时域有限差分
时域有限差分(FDTD)可以理解为有限差分的一种,由于求解思想天然符合电磁场传播特性,是求解电磁问题的一种有效方法。在求解空间分布各向正交连续点网格(Grid),通过时间上电磁节点不断交替前进求解每个节点数值。该方法主要计算量集中在时域上每个节点的迭代,整体框架上不需要求解线性方程组。(点击链接查看)一篇文章入门时域有限差分方法(FDTD)
3.边界元(BEM)/矩量法(MOM)
边界元是一种将网格划分在边界上的求解方法,也就是三维计算只需面网格,二维计算只需线网格。边界元是一种数值解和解析解结合的方法,计算需满足一定条件。借助于解析解,可以大幅减少最终线性方程组的规模。但最方程组的系数矩阵一般满秩,需要借助快速多极子,多层快速多级子等方法提升求解效率,加大了开发难度。矩量法也是一种半解析半数值解法,最终形成的也是满秩矩阵。一篇文章入门边界元方法
4. 有限体积(FVM)
基本思路是:将计算区域划分为一系列不重复的控制体积,并使每个网格点周围有一个控制体积;将待解的微分方程对每一个控制体积积分,便得出一组离散方程。其中的未知数是网格点上的因变量的数值。为了求出控制体积的积分,必须假定值在网格点之间的变化规律,即假设值的分段的分布的分布剖面。目前主流商业CFD软件都使用FVM方法。
5.格子玻尔兹曼(LBM)
LBM是最近十几年逐渐在工程领域流行的求解CFD问题的方法。该方法在介观尺度离散玻尔兹曼方程,不需要划分网格,并且易于并行化,前处理效率高,在一些非常规CFD计算领域有较高的计算精度,是一种典型的无网格方法。一篇文章入门格子玻尔兹曼方法(LBM)
4. 求解器框架设计
框架设计,并不强调某种数值计算方法或算法的代码实现,也不看重单个求解方法或第三方库的性能,这些因素对框架设计会有影响,但框架设计的需求是考虑如下问题:
如何保证长期持续稳定开发
长期开发意味着:开发人员可能会频繁流动,新开发人员接手项目是常事,最为典型的是高校的一些程序开发,一个项目开始后,往往由临近毕业学生参与,贡献一部分代码毕业后,则由下一届接手。这里最大的问题就是新开发人员需要在理解业务读懂源码的基础上才能进行新的工作。原程序框架决定了新开发工作效率。一个好的框架设计,可以让新研发人员方便地添加和修改功能。
2.第三方工具和求解器某种功能交互接口
考虑以下几种情况:
2.1.需要把求解器某种功能放到前处理器中。比如网格检查功能,前处理仅仅能从网格质量,拓扑来检查网格数据,而求解器可以从业务,仿真计算角度检查网格数据。可以直接把这块功能搬到前处理功能中,提前检查出错误。
2.2.自适应迭代网格。参考
自适应网格的一次迭代是一次完整的计算流程。如果我们使用不同的加密策略,或者使用第三方软件进行加密操作,要求每次计算流程是一个独立的模块或组件,能方便外部功能调用。
2.3.优化设计。优化设计也是经常提到的,它和生成式设计,CAD/CAE无缝集成等也紧密相关。利用仿真进行优化设计的核心是外部程序不断调用求解器,以期获得输入参数和结果的关系,非常类似神经网络训练,或者就是神经网络的一种。
以上这些操作都需要把求解器中的一个或多个功能作为一个独立的组件和模块使用,独立的组件也就是不依赖任何第三方组件,在程序中是只被调用而不用调用其它模块。在数据和工程依赖上,就要求定义好接口和API,做好模块封装。
下图列举了一些求解器常用模块和相互依赖关系,供参考
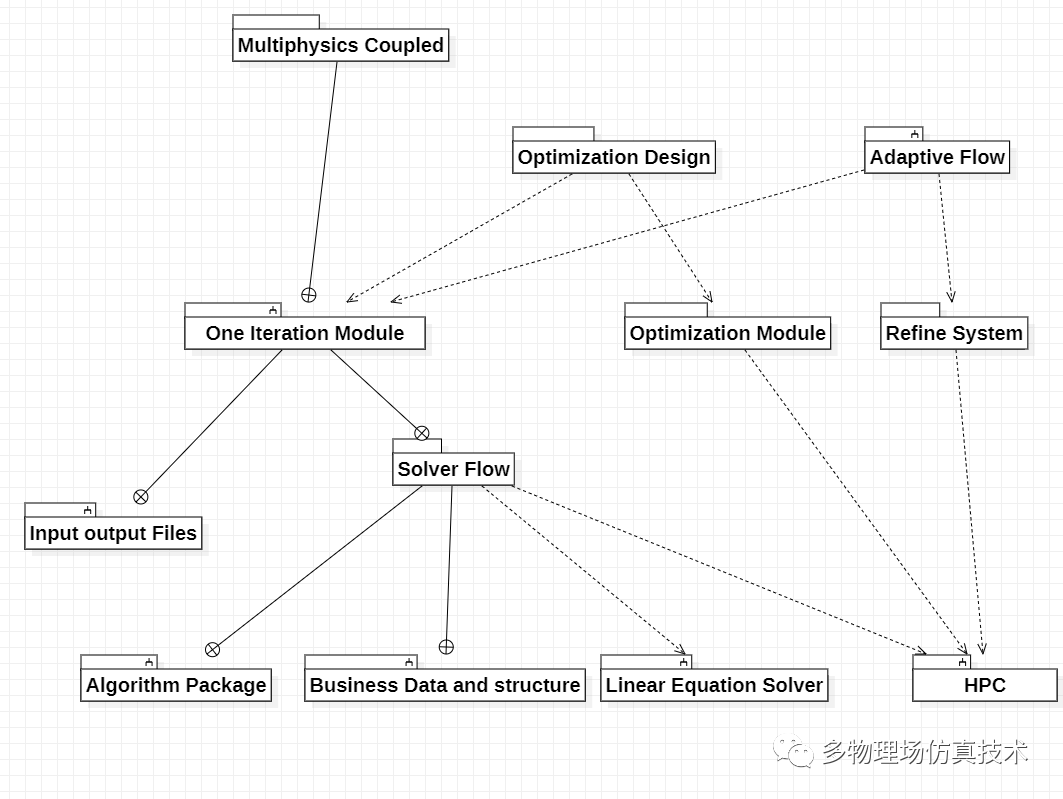
模块依赖关系
从整体研发角度看,开发可以根据模块划分成几个部分:
1. 数据结构和算法部分;
2. 架构设计;
3. 前后处理(这里指的是求解器内部的前后处理)
4. 测试用例和应用
5. 第三方库调用(比如线性方程组求解)
对于大多数研发人员,可能认为算法是最重要的部分,实际上对商业软件而言,架构和算法同样重要。
3.研发需求持续更新
数值模型求解中,边界条件是一块大的内容,在求解器开发中,开始会支持一些简单的边界条件,后续再根据实际情况逐渐增加。其它内容比如材料,单元,激励荷载,物理模型等也有相同的情况。这就要求我们在最初设计时,考虑到这些更新需求。
以CFD边界为例,OpenFOAM中的边界条件多达数十种,参考
一篇文章入门计算流体动力学CFD--(上)(点击链接查看)
而电磁场中,仅以高频电磁电路仿真为例,边界条件和激励也多达十多种。后续会专门一文介绍高频电磁场中的边界条件。
我们在开发之初不太可能全部支持这些边界条件,会根据实现难易程度,用户使用情况来逐步完善边界,荷载,激励的支持。
4.工具和技术持续更新
我们常用的第三方库,开发工具,开发系统平台等,都一直在更新。求解器框架的设计需要尽可能独立于这些内容。求解器一般在Linux上有更好的性能表现,在Windows上开发,Linux使用是常态,有些需要直接在Linux平台上开发。所以有些只支持某些特定平台的工具或第三方库就不能使用,需要考虑平台的通用性和跨平台。
在需要求解线性方程组的求解器中,我们一般不会自己写算法求解,而是调用已有的成熟工具库。工具库内容繁多,各有各的特点。所以根据自己的业务选择合适的库就很重要,此外求解内容一般和矩阵数据特点紧密相关,而矩阵数据由业务内容决定。所以需要在实践中确定合适的计算库和方法。
工具和技术持续更新,这种更新不单是工具层面,而且还有基础技术层面。比如出现的GPU,MIC计算架构,新的开发语言出现。早期的数值计算语言都为Fortran和C,后来工程化代码普遍使用C++,某些上层的计算应用可以使用Python。这些在框架设计支持之初就是需要考虑的。
5. 单独算法封装
多物理场仿真研发中,一般以单物理场为主,比如流体,热,声,结构静动力,电磁。在这些单物理场分析中,会细分出很多求解类型,仅以动力学为例(结构动力学,刚体动力学,转子动力学,微观动力学,电动力学,气动弹性等),每种求解类型结合实际业务,会衍生出各种求解工况和实际模型,对于几何异形,自由度高,工况复杂,多材料,多尺度,非线性强的单一物理场问题,并不比一般的多物理场问题容易。正是因为实际单物理场问题的复杂度高,所以在求解多物理场耦合时,不得不做出很多简化和假设,这也是多物理场耦合仿真精度不高的一大原因。
5.1.材料表面粗糙度
一个看起来和电路仿真没有关系的内容,在高频电磁仿真的时候,对仿真精度的影响不能忽视。对于直流电路和低频仿真,材料表面粗糙度不会对仿真产生影响。但在高频交流电时,由于趋肤效应,电流会集中到金属表面,频率越高,电流集中程度越高,也就是电流只会从金属表面流过。这时金属表面的粗糙程度会对电流产生较大影响,从而影响电阻等电器特性。同时随着频率的升高,电阻,电容电感等特性都会产生非线性变化,加大了电路求解的难度。所以高频电磁的求解普遍采用场方式。
5.2."SIMPLE"不Simple
SIMPLE算法,全名为压力耦合方程组的半隐式方法(Semi-Implicit Method for Pressure Linked Equations),是计算流体力学(CFD)中一种被广泛使用的求解流场的数值方法,于1972年由苏哈斯·帕坦卡与布莱恩·斯波尔丁提出。
在SIMPLE算法基础上,又出现了很多改进版本,常见的有:
1.SIMPLE Revised,缩写SIMPLER,即将速度修正和压力修正使用不同的方法。
2.SIMPLE Consistent,缩写SIMPLEC,SIMPLEC和SIMPLE算法步骤相同,只是速度修正方程中系数项的计算不同。
3.PISO,Pressure Implicit with
Splitting of Operators
相比SIMPLE,PISO需要两次求解压力修正方程。在实践中,对于瞬态问题,PISO算法有一定优势。
SIMPLE系列算法作为一种CFD基础算法,一般的商业软件都有支持。
5.3.结构非线性
非线性是结构分析中的一大痛点,非线性通常来源于:
1.材料非线性:典型塑性变形,各向异性材料;
2.边界非线性:在分析中,边界条件发生变化,就会产生边界非线性。典型的碰撞,冲击,接触分析;
3.几何非线性:大变形,大挠度,初应力和荷载刚化。
多物理场耦合一般两种:弱耦合和强耦合。弱耦合的方法是首先求出一种物理场的结果,然后将结果作为输入加载到另一物理场上,迭代计算。这种方法相比强耦合,简单可靠,可以充分发挥单物理场求解的优势。使用弱耦合的方法就要求算法封装性要好,能容易的调用以及扩展。
5. 网格文件设计
对于需要使用网格的数值计算方法,前处理器需要设计网格的数据格式和文件格式。在商业软件开发中,尽可能参考类似Nastran BDF以及ABAQUS INP文件格式,而不要使用开源软件的文件设计。主要原因是开源软件设计不会考虑扩展性和性能问题,如果使用开源软件结构,在商业软件后期开发中是个非常大的瓶颈。
在数据结构设计上,可以参考
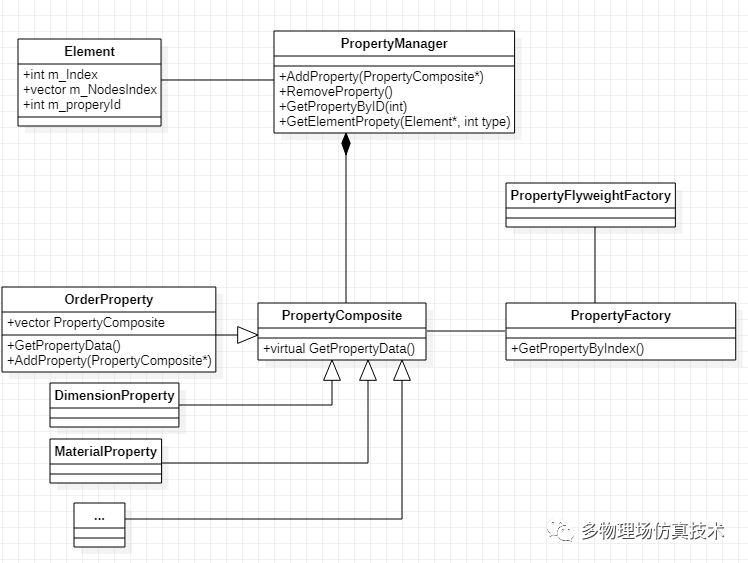
该模式中的数据结构,可以作为使用网格计算方法的通用网格数据结构。其核心是用Composite和flyweight方法管理各种属性,包括单元属性,边界属性,荷载属性,材料属性等等,将各种属性数据和网格结构解耦。
网格数据通常包含两部分,
第一部分是网格坐标和拓扑数据,以下多种或其中几种:
坐标点
边拓扑数据
面拓扑数据
实体拓扑数据
单元数据
第二部分是各种单元,边界,荷载,材料属性实际数据。
边界,荷载,材料属性可以任意附加在点,边,面,实体和单元数据上。这种属性附加通常使用索引方式映射生成。
在文件存储方法上,两部分数据可以放在一个文件里,也可以分开存放,各有优缺点。从解耦角度看,分开存放更合适;从数据完整性角度看,放在一起方便模型处理。可根据实际情况选择。
网格文件的读写功能可以做成基础模块,供第三方调用,由前处理器负责,求解器方也可以使用,但从模块划分和解耦角度看,求解器方的网格解析最好由求解器来做,原因在于求解器和前处理器的网格数据结构有很大不同,如果使用统一模块,求解器要做二次转换;在解析过程中,求解器可能还有调试需求。
为了避免模型文件被非法查看,网格文件在调试时可以使用文本文件,真正调用时使用二进制文件,并进行适当加密。需要注意的是网格文件的拓扑数据需要固定字段长度,否则大模型读取解析性能会有问题。
6. 基础数据结构
常用的数据结构包括:
Vertex 点
Vector 向量
Tensor 张量
Matrix 矩阵
Complex 复数
以及基于这些类的扩展类。
针对某些高精度计算,需要使用类似GMP的高精度库。
按照单一职责原则,每种基础数据结构提供基本的数据,数据和数据之间的计算由另外的工具类提供。考虑到求解器的数据规模,在设计定义数据之初,须使用数据指针,并避免数据之间深拷贝。
矩阵结构定义

Eigen库提供了很多基本数据结构,可以直接使用,但从性能,效率以及扩展性看并不最优。如果是商业软件开发,基础数据结构最好自己定义。
7. 线性方程组求解
对于很多求解器来说,常用的
FEM,FVM,MOM,BEM等需要求解线性方程组。求解线性方程组一般不会自己写,而是调用一些已有的求解库。关于线性方程组的求解也一直是公 众号介绍的重点,参考
两本线性方程组相关书籍pdf下载
除了以上专门介绍的线性方程组解法,在求解器相关内容介绍中,也通常会顺带介绍某些特殊的解法。
关于线性方程组求解库的选择,之前有过推荐:
入门Eigen
根据实际情况,可用MKL, OpenBlas,MUMPS
其它一些比如PETSc,Hypre,Trillion等稍重量级的也可以试用
某些专门加速的商业库也可以使用
如果是需要长期从事线性方程组求解工作的,建议可以从最基础的求解库
BLAS,LAPACK,ScaLPAPCK用起,很多使用第三方库碰到的问题和疑惑,根源都能从这些基础库里找到答案。另外很多比较老的库也可以使用,比如SuiteSparse,SuperLu,Pardiso,TAUCS等,了解每种库的使用特点以及适用范围。
方程组求解的准确以及性能,和矩阵的数据特点,矩阵规模,硬件环境紧密相关。需要注意的是,在数据结构上做好封装,方便调用不同库之间进行切换。
在这一块如果有继续深入研究需求的话,一方面需要牢固的线性代数,矩阵运算基本功,另外对硬件知识,C++高性能计算也要比较熟练。高性能计算普遍在Linux环境上进行,熟悉类Linux环境是基本功。
8. 调试
曾经碰到这样一个问题,在对矩阵进行LU分解后,组装矩阵求解线性方程组时,求解库一直报错矩阵非正定,在确定流程,业务数据和求解库没有问题后,最后只能从矩阵本身查找问题。在用尽所有调试方法之后,最终发现原因是个非常低级的错误:矩阵的上三角和下三角都包含对角矩阵,导致对角矩阵被加了两次。
求解器研发的两大特点,一是数据量大,运行一次整个流程时间普遍较长;二是运行以数据处理为主,以控制台方式运行,没有GUI。一旦数据出错,很难调试,尤其是第三方工具求解出错时,原因可能是数值计算,业务逻辑,或者数据本身问题等等。数值计算和数据本身出错可能还容易点,而业务逻辑问题导致最后矩阵出错,几乎没有方法调试。
所以需要有针对性的提供调试工具。最常见的比如要导出MATLAB等数学工具支持的文件,方便导入MATLAB中分析调试;通过GUI等工具合理控制运行步骤;提供不同方法的数据对比机制,动态监控内存,CPU,网络等硬件资源消耗;建立最基本的回归测试机制等。
9. 开源和商用比较:
以下案例为虚构,如有雷同,纯属巧合,背景如下:
公司开发了一款使用有限元方法计算的仿真软件,一年发一正式版
有一个案例,上一年,用户使用该软件产品可以跑出正确结果,但是今年的版本跑出的结果不对
案例只能在用户的服务器上跑,案例文件拿不出来
因为案例比较大,一天流程只能跑一次
答应解决该问题就续签服务合同,合同一百多万刀
老客户,给了最多一个月时间解决
如果你是项目负责人,如何解决该问题?
参考:(点击链接查看)
仿真软件研发问题讨论(解决方法)

当我们谈论求解器开发时,默认目标是商用求解器,也就是能给用户实际使用并解决计算问题的工具。原型开发里的求解器原型以及大部分开源求解器是无法达到这个要求的,这两类求解器和商用求解器之间还是存在一道较大的鸿沟,直接具体表现在以下:
1.业务方面:
1.1.实际模型模拟近似程度
这是求解器研发的核心,我们知道求解器的原理其实都是公开的,所以从代码实现角度讲,并没有太大难度。理论计算分析实际上是有很多假设和前提的,和实际的模型并不是完全匹配,比如结构分析中出现的应力集中,沙漏,死锁和实际模型并不吻合,这时候需要特殊处理,而不能简单的忽略。高频电路电磁仿真中,频率高到一定程度,其金属表面粗糙度会对电流产生较大影响,就不能忽略。对于分析中的这些假设,前提,误差等需要详细处理,才能满足实际工程计算要求。
对于一些计算参数的选择,商业软件是经历了详细测试以及用户迭代的。这些参数作为黑盒子封装在底层。比如根据模型,选择时间步长,网格尺寸,收敛标准,线性方程组求解方法和参数等等。
1.2.对网格依赖程度
一些资深工程师应该有这种体会:同一套网格,有些商业软件能算,有些商业或开源求解器算不了;有些划的质量很差,看上去就不容易收敛的网格,在某些商业软件里居然能跑出结果。这里面其实是商业软件做了大量工作,对网格和计算做了很多优化,具体内容后面有空再介绍。
1.3.前后处理程序
求解器一般作为单独程序存在,但是好的前后处理程序可以提升求解器的使用效率。比如好的网格质量,快速结果查询显示,参数扫描,优化设计等等。
2.计算方面:
2.1.准确性,稳定性
商业软件一般要给实际客户使用,且需要完成设计仿真周期,因此必须要做大量的基础Benchmark,并且经历过实践和用户迭代,准确性和稳定性是基本要求。
因为实际模型和计算模型天然存在误差,所以计算结果不可能和实验结果完全一致,这里就涉及到另一个话题:如何让仿真结果可靠。从软件角度看,常用的方法就是调参,调主要的参数,看计算结果趋势波动是否和实验保持一致。
2.2.速度和效率
在满足准确性和稳定性基础上,计算速度效率也很重要。软件方法,求解器的速度主要体现在算法优化上,根据实际业务和硬件改进算法。软件方面,多线程和分布式计算是最基础的,把主要计算放在大的服务器上,提供资源调度分配;更进一步,根据硬件编译底层程序。除此之外,对堆硬件提供更好的软件支持以支持分布和并发。在这一块,基本很少看到开源软件提供支持,能跑一下OpenMPI就非常不错了。
2.3.新技术的使用
工业仿真软件技术上大的突破,求解器使用GPU异构计算应该是一个。在2007年左右,CUDA发布之后2,3年内,几乎主流的工业仿真软件都提供了GPU计算支持,少有开源软件支持。

在“求解器”开发入门指南(上) 一文中也给出了求解器的一些具体标准:

10. 求解器研发的难易程度
经常说求解器是核心,难度最高。根据经验,将求解器开发难度由简到难分为四层,需要说明的是这四个层次并不完全独立,而是相互有关联,其实任何工业软件工程问题都可以从这四个方面考量:
算法实现难度
算法实现也就是通常所说的理论实现,即将数值计算方法理论用代码实现。比如我们常用的FEM,FVM,LBM等。需要理解数值计算原理,实现一个基本求解器原型。大部分书籍教程也是围绕这块在讲,属于入门级别难度。我们在书籍和自媒体经常看到很多相关计算理论介绍,各种生僻看似高深算法参数名词,不用被吓到,这些都是最基本的理论知识,了解后记住大概意思即可。比如FDTD, 本质上就是一个多重循环(2维是个双循环,3维是3层循环),在不同维度迭代更新E和H。CFD里看似高大上的湍流模型,常用的就k-e,k-o系列那么几个,参数记不住的话,列个表用的时候查。各种偏微分方程理论,公式推导理解记住最好,记不住也没关系。
总之这块是求解器基础知识,基础越扎实越好。对于研发而言,没必要在这个层次花过多时间,也不用太纠结很多细节问题和理论公式。
2.业务实现难度
业务实现,一句话概括就是尽可能准确,精确,高效的求解计算模型。
1.要准确的计算模型,就需要精准的支持各种荷载,边界,各行业独有的物理特性等数值计算理论。
工业仿真软件主要求解的是偏微分方程,根据PDE理论,常用的边界条件就三类。在实际应用中,边界条件的设定几十种都很常见,主要原因是各种边界条件有其适合的场景,这种场景是综合考虑了求解模型特点,计算精度,算法和参数适应场景,操作便捷程度,实际工程等各种因素,一般的开源软件不会考虑的。
来看ChatGPT回答的OpenFOAM的二十种边界条件
1.入口边界条件 - 用于指定入口速度,质量流量率或压力
2.出口边界条件 - 用于指定出口压力或仪表压力
3.墙边界条件 - 用于模拟无滑动或自由滑动条件的固体墙
4.对称边界条件 - 用于模拟对称平面或轴对称几何体
5.空边界条件 - 用于从特定区域中删除流体
6.压力远场边界条件 - 用于模拟远离计算域的压力场
7.速度入口边界条件 - 用于指定入口边界的速度
8.出流边界条件 - 用于指定出流速度
9.FixedValue边界条件 - 用于指定特定字段(如温度)的固定值
10.滑动边界条件 - 用于模拟墙上部分滑动的条件
11.诺依曼边界条件 - 用于指定边界上字段的导数
12.自由流边界条件 - 用于指定自由流的条件
13.总压边界条件 - 用于指定入口或出口的总压
14.总温度边界条件 - 用于指定入口或出口的总温度
15.热流边界条件 - 用于指定热流条件,如热源或冷却器
16.紊流边界条件 - 用于模拟紊流或高紊流条件
17.超声速边界条件 - 用于模拟超声速流体的条件
18.固定墙边界条件 - 用于模拟固定的固体墙
19.温度边界条件 - 用于指定特定的温度条件
20.自适应边界条件 - 用于模拟动态变化的边界条件
对应OpenFOAM实际边界:OpenFOAM 边界条件简介(点击链接查看)
2.支持各种新的计算模型,比如新材料特性,新单元类型,新计算参数,前沿计算方法,新的湍流模型等等
3.和第三方工具做benchmark,横向验证求解器质量
4.目前求解大规模线性方程组并没有一种通用的高效方法,研发中往往需要根据实际业务需求选择。这块也是一直作为重点在介绍,有专题,也零散的讲解。这块理论了解后就是实践,目前商业软件的求解方法也是在实践的基础上封装成黑盒使用。研发除了长期积累经验外,似乎没有太多有效的方法。
5.多物理场耦合,各种多物理场耦合模型仍然是求解器开发的难点,涉及新理论,计算精度,耦合方式等等
6. 高性能计算支持(HPC)
从技术角度看,相比各种开源求解器,这块内容是商业求解器真正产生价值的地方。
3.模块复杂度
模快复杂度更偏向于软件架构设计层面内容。其核心在于将求解器各个算法,功能进行合理拆分,封装,在满足基础算法的基础上便于软件架构层面的管理。方便测试,扩展,调试等整体操作。
在为什么求解器开发需要强势使用设计模式(点击链接查看)一文中也强调了商用求解器开发的这种特点。这块功能的开发不仅需要对算法,软件工程比较了解,对业务也要有较深入理解。业务很大程度上决定了求解器长期的发展方向。
这块的工作内容主要对应于软件架构。看到有些公司招聘互联网行业的软件架构师做求解器设计。虽然职位都是软件架构师,其实是两个完全不同的概念,注意一下。
长期看,求解器研发一定是要模块化的,这种模块化体现在各个层面:基本代码单元,代码组件,功能模块,架构模块,产品层面。很多时候,因为开发人员水平,成本控制,业务需求等客观原因,导致在规划阶段做的不足,模块化没做好,后续要花投入更多时间精力来修正和弥补。
“屎山”通常指难以修改,有层出不穷的bug,只有写代码的程序员本人才看得懂,并且历史悠久,行数巨大的代码。很多老牌工业软件公司的代码最长有四五十年历史,短一些一二十年也是有的。如何维护支持这些求解器代码也是公司非常头疼的问题。曾经一家CAE大厂试图用C++重写用Fortran开发了近三十年的求解器,一年之后种种原因不得不放弃,改为维护原有代码,只做了小范围的重构,原因大概率是陷入“屎山”不能自拔。前后处理器因为本身依赖第三方组件,且很多功能相对独立,维护重构或者重做相对容易。
对于求解器开发人员,不仅要学习数学物理算法,还有必要学一些软件工程的内容,能帮助算法层面的实现,有利于提高开发效率,避免不必要的重写和重构。
4.系统复杂度
在前面123的基础上,这里就是经常所讲的系统工程阶段。这块核心并不是研发本身,而更看重非技术因素,主要目的是让求解器能够使产品真正产生价值。就如最开始介绍的案例,如何在保密的客户机器上进行调试,生成结果,让用户以最低成本用好软件;在各种软硬件环境下运行程序;如何利用软件产品帮助客户完成各种设计,验证,或者测试要求。
在实际应用阶段,很多问题都是工程问题,而不是简单的技术问题。一句话概括,就是实际工程问题会受限于成本,软硬件环境,用户水平,工期,实际案例缺陷等诸多非技术因素,在综合考虑这些因素后找到合理的解决方案。
从系统工程角度看,这一层的求解器已经不是单纯的程序开发,而是作为工具,如何让产品服务客户,产生价值。


1. 以稀疏矩阵的行或列为节点,构建相应的图结构;
2. 使用METIS进行图分割,将整个图分割成若干个不相交的子图;
3. 利用某种并行求解算法对每个子图进行求解,得到每个子图的解向量;
4. 通过合并各个子图的解向量,获取原始方程组的解向量。
METIS采用的基本策略是贪心策略,即从某个起点开始依次选择邻居节点来构建连通块,并对连通块进行规模划分,METIS通常采用四种划分策略:k-way、recursive k-way、refinement、和 time-limit 限制策略;METIS适用于稀疏、规则性数据较强的场合,而对于高度粗糙数据其效果可能不佳。此外,还要根据实际问题进行参数选择和优化,比如选定合适的划分方法、块数,需要一定的经验。
线性方程组求解的敏感度分析主要研究输入数据、参数误差对方程组解的影响。一般而言,可通过以下步骤实现:
1. 对输入数据/参数进行微小改变,如增加或减小一个较小的扰动
2. 计算新方程组的解,并与原来的解进行比较
3. 评估解的相对变化与参数扰动之间的关系
MpCCI接口软件可以实现不同模拟软件耦合区域的网格量的数据交换。由于耦合区域网格通常属于不同模拟程序,一般而言这些网格是不匹配的,MpCCI在实现网格值的数据交换前,先执行节点值之间的插值,求解器研发可以作为参考
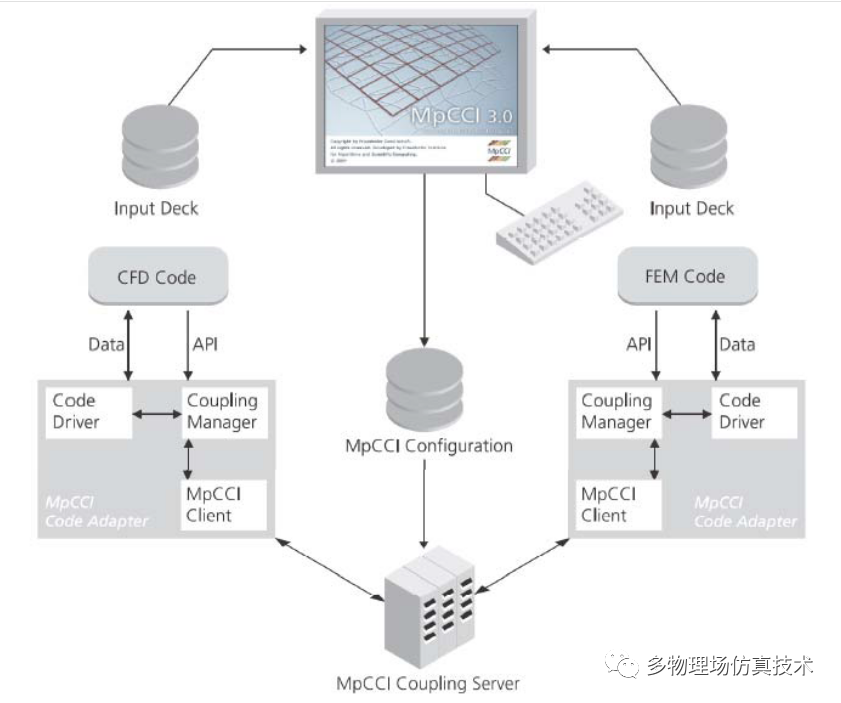

(Nonlinear Programming by Quadratic Lagrangian)是一种非线性规划算法,其思想是通过构造一个二次Lagrange函数来求解非线性的无约束优化问题。
NLPQL 算法的输入参数通常包括以下几个核心参数:
1.目标函数:这是需要最小化的非线性目标函数,通常由变量X和系数向量C组成。用户需要在此处指定待优化的问题及其目标函数
2.限制条件(约束条件):这些为目标函数的一组限制条件,对于规划问题来说可能包括若干限制等式和不等式。如果存在限制条件,则需要将他们与目标函数一块考虑进去来求解
3.初始点(起始点):这个参数描述最初用于迭代优化的 X 向量的初始值。这通常是一个采样分布或模型预测的结果,可影响到最后的优化结果
4.单步容差控制:控制收敛精度的一个数字容差参数,表明前后两次迭代 向量值的最大单项相对变化,该参数决定了算法是否停止迭代
5.目标函数评估TolFun:表示算法收敛时重复求解目标函数C的价值,在二次 lagrangian 时每次计算步骤后,价值变化的最大相对变化量为此参数
实际业务中的模型往往是大模型乃至超大模型,公 众号关于这块也是详细介绍的内容,目前关于超大模型的求解器部分内容:
相关文章,在仿真秀官网搜索:




