数据驱动力学(Data-driven mechanics)最新研究进展
文一:

计算力学中的数据驱动游戏
摘要:
我们采用博弈论来制定固体力学的数据驱动方法,在这种方法中,应力和应变参与者追求不同的目标。应力播放器的目标是最大限度地减少与材料数据集的差异,而应变播放器的目标则是从相容性和平衡的意义上确保机械状态的可容许性。我们发现,与过去提出的合作数据驱动博弈不同,新的非合作数据驱动对策从数据中识别出一个有效的物质定律,并将其归结为传统的位移边值问题,这有利于其实际实现。然而,与有监督的机器学习方法不同,所提出的非合作数据驱动游戏是无监督的、无模拟的和无参数的。特别是,有效物质定律是直接从数据中学习的,而不需要回归到一类参数化的函数,如神经网络。我们给出的分析阐明了数据驱动解决方案相对于数据收敛的充分条件。我们还介绍了选定的实施和应用示例,这些示例展示了该方法的范围和多功能性。

图:两种数据融合场景。(a) 一致收敛:数据包含在极限应力-应变图周围越来越窄的误差带内,并以不断增加的密度对该误差带进行均匀采样。(b) 带异常值的噪声数据:数据越来越集中在极限应力-应变图周围,但表现出分散和异常值。
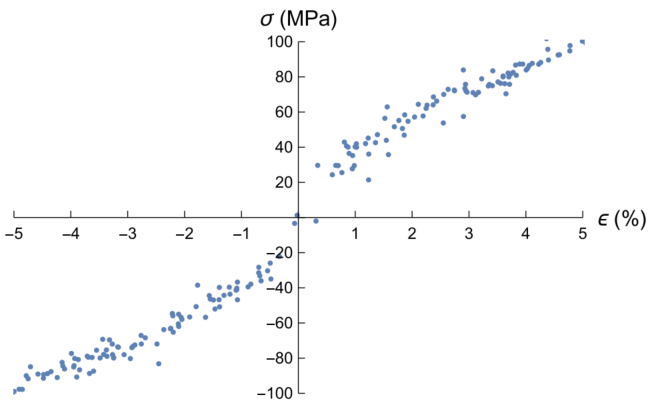
图:200个数据点集。应变是均匀分布的,通过在极限应力-应变曲线上添加随机高斯噪声来获得数据点。
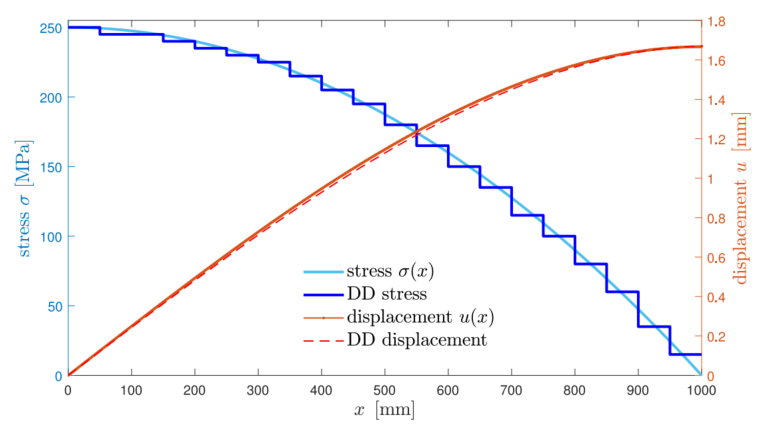
图:旋转杆问题离散为20个等线性有限元
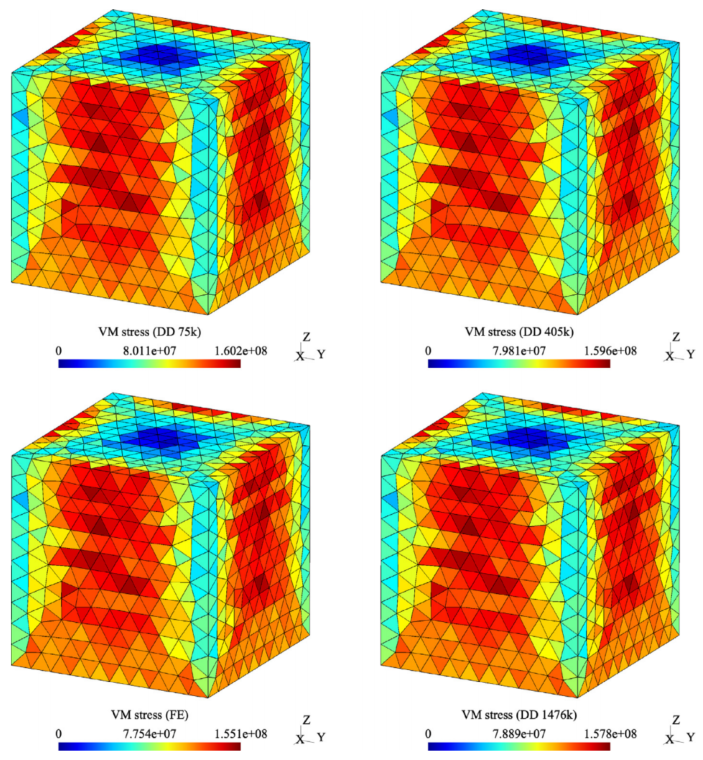
图:非线性弹性立方体的扭转,等效冯-米塞斯应变。顺时针:适用于75,625、405,769和1,476,225,以及参考有限元解。
文二:

数据驱动的破碎力学:预测颗粒介质中颗粒尺寸分布的演变
摘要:
本文提出了一个无模型数据驱动的断裂力学框架。与连续体断裂力学(可压碎颗粒介质宏观分析的事实方法)相比,本框架不需要定义本构模型和唯象假设,依赖于仅通过经验数据已知的材料行为。为此,我们回顾了历史相关材料的无模型数据驱动计算的最新发展,并将主要思想扩展到具有颗粒破碎的材料。从连续体断裂力学的闭式表示开始,提出了建模框架的系统结构,并得出了替代的无模型表示。强调了数据驱动框架的预测能力,并将其与连续体断裂力学在不同边值问题上进行了对比。此外,还介绍了可压碎砂的实际实验测试的应用,其中数据是通过高保真度颗粒尺度模拟提供的,表明所提出的框架提供了对可压碎材料力学(包括粉碎状态)的准确预测。
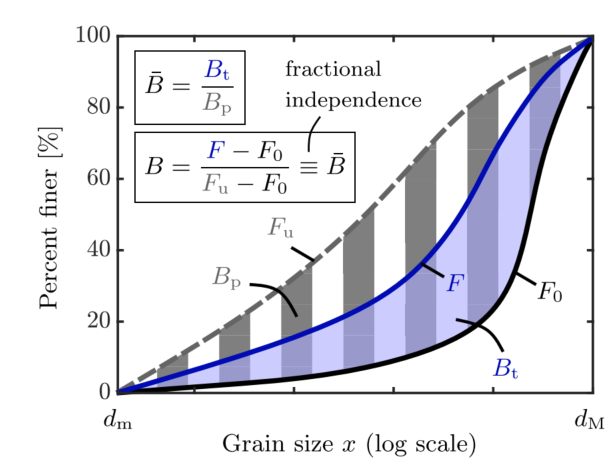
图:不断发展的GSD。
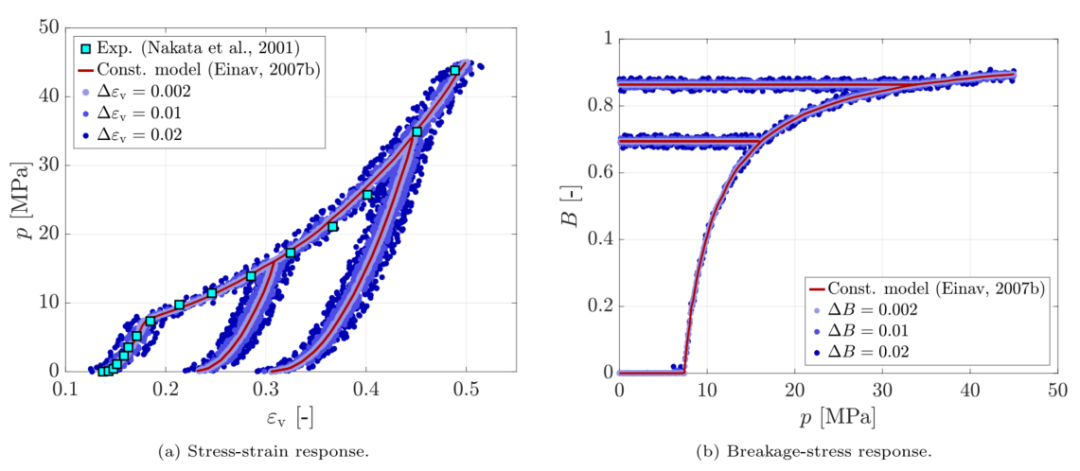
图:本构破坏模型的响应及其与实验结果的比较
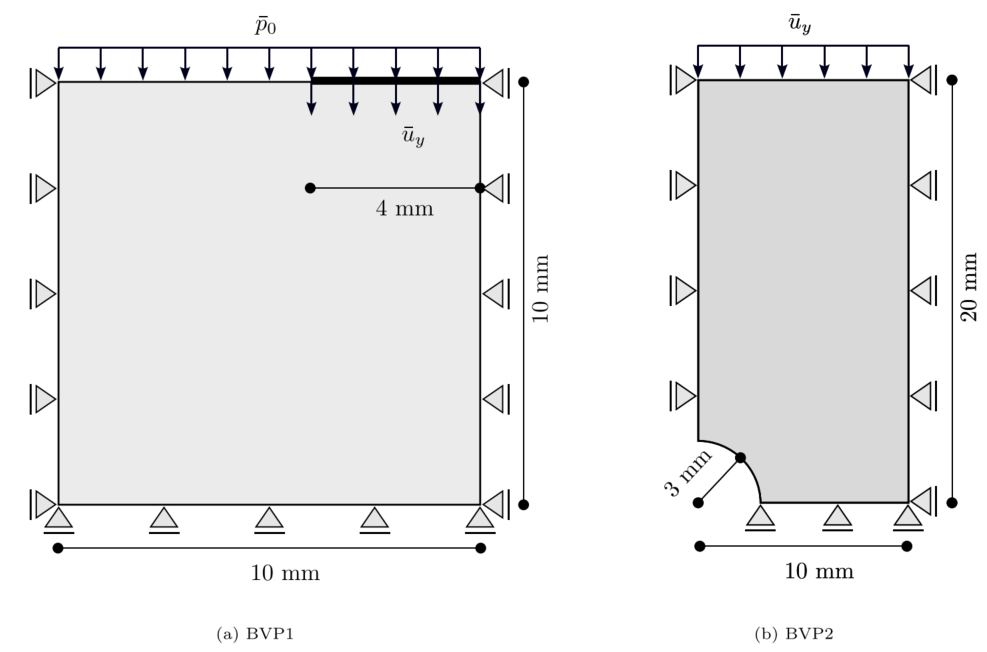
图:数值模拟中考虑的边值问题的示意图。
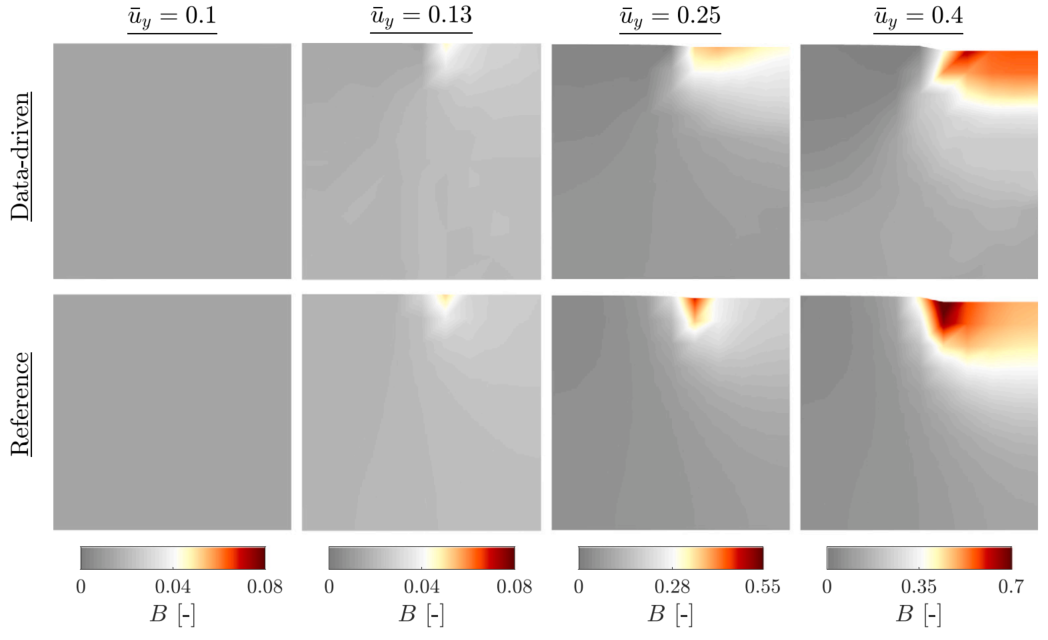
图:BVP1断裂场的快照,将用BVP2(顶部)的数据获得的数据驱动解决方案与连续体断裂力学(底部)的参考解决方案进行比较。
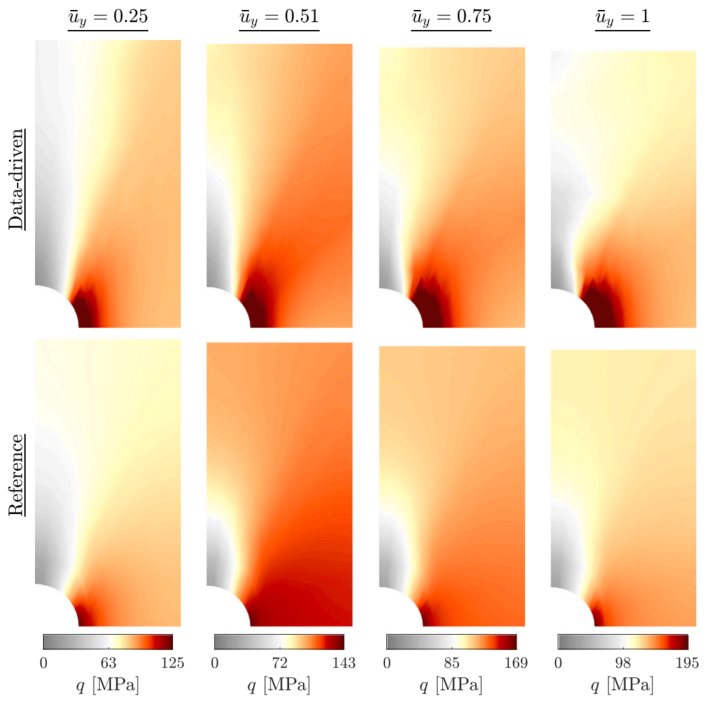
图:BVP2剪切应力不变场的快照,将用BVP1数据获得的数据驱动解(顶部)与连续介质断裂力学的参考解(底部)进行比较。”
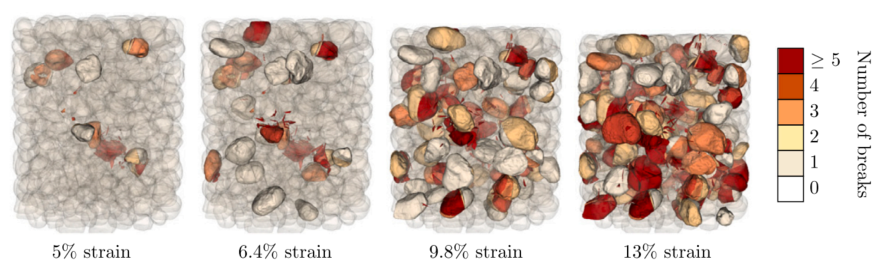
图:LS-DEM模拟的Oedometer试验结果显示了不同载荷下虚拟试样的断裂演变阶段。

图:数据驱动计算的结果(左)和连续体断裂力学的结果(右)显示了GSD在单调加载的不同阶段的演变。将结果与参考LS-DEM模拟和实验测量结果进行了比较。
文三:

网格d精细化:一种基于数据的计算框架,用于解释复杂的材料响应
摘要:
无模型数据驱动计算力学(DDCM)是固体力学模拟的一种新范式。通过引入抽象相空间来规避与材料本构定律定义相关的建模步骤,在该抽象相空间中,遵循预定义规则,物理可容许状态与观察到的材料响应数据(来自实验或低规模模拟)相匹配。就计算资源而言,执行这些匹配的搜索过程是算法中最繁重的步骤。DDCM的主要优点之一是避免了基于回归的、倾向于偏差的本构模型。然而,许多材料在小应变状态下确实表现出简单的线性响应,同时在一定的变形阈值后也表现出复杂的行为。受这一事实的启发,我们提出了一种新的细化技术,如果规则单元(配备线性弹性本构定律)有望超过触发材料非线性响应的已知阈值,则将其转化为数据驱动单元。我们将这种技术称为“数据细化”,简称“重新定义”。它既适用于基于DDCM的数据驱动元素,也适用于使用神经网络从数据中学习的应变-应力关系。从最初的规则FEM网格开始,所提出的算法检测哪里需要细化,并迭代,直到所有被认为显示非线性的元素变成数据驱动的元素。讨论了插入标准。该方案非常适合于在域的相对较小部分中具有非线性响应的模拟,而其余部分保持线性弹性。该方法与传统的增量求解器(即牛顿-拉斐森方法)进行了验证,我们表明d精化框架在不损失精度的情况下,在速度方面优于它。我们提供了一个应用程序,展示了新方法的优势:建筑超材料中的桥接尺度。对于这个应用程序,我们还简要介绍了如何将d-精化与在微尺度数据上训练的神经网络结合使用。
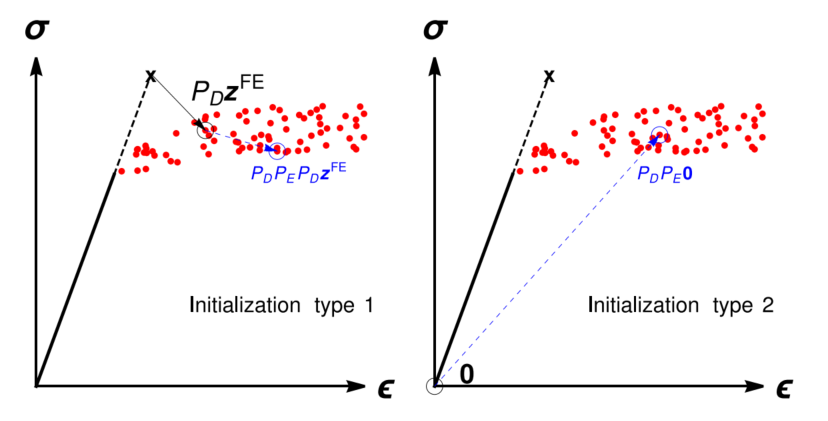
图:2D相位空间上DD元件初始化可能性的示意图。第一个圆圈(黑色)表示初始化点,第二个圆圈(蓝色)表示数据集中算法在下一次迭代中收敛到的点(请注意,每次迭代后,每个方法都可以选择不同的数据)。
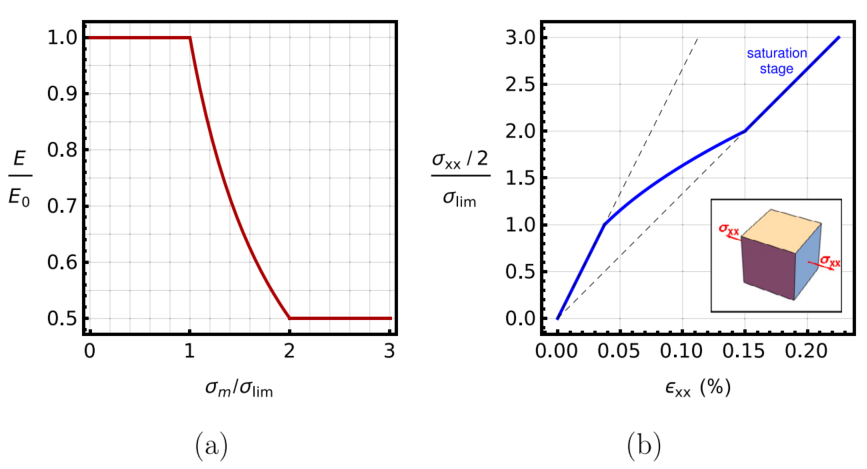
图:可视化模型的材料响应;(a) 随着平均应力的增加,刚度损失。(b) 单轴加载的应力-应变关系。

图:三点弯曲配置方案。箭头表示在顶部中间节点处施加的位移。
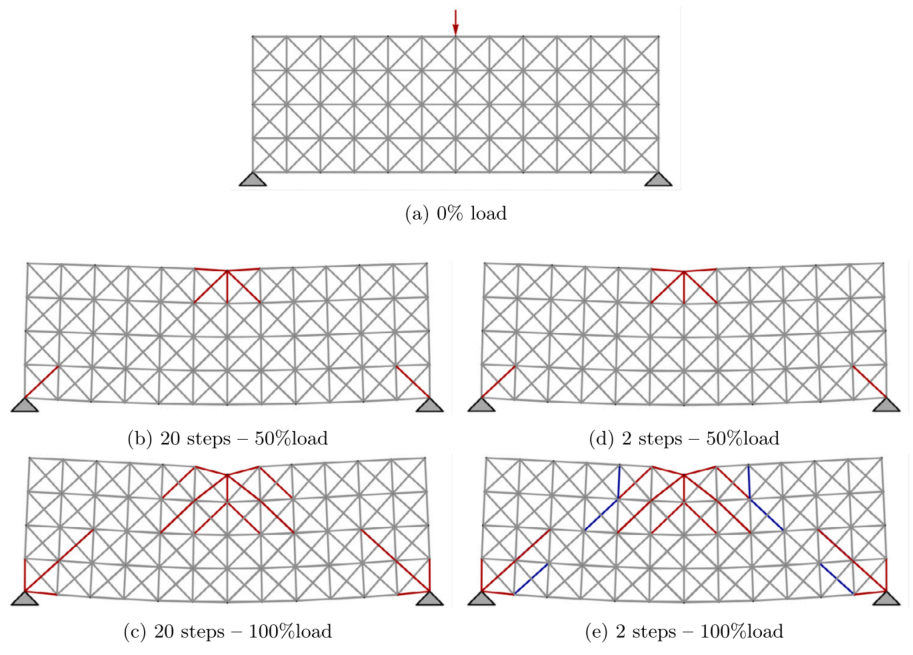
图:梁桁架在二维平面上的投影。右栏描述了用2步加载获得的结果,而左栏描述了20步加载的结果。在红色中,应为和已细化的单元。在蓝色中,指不必要地细化的单元。
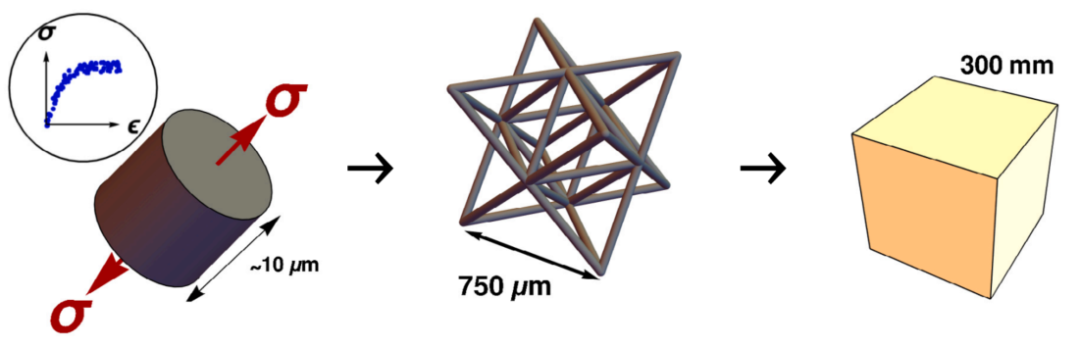
图:尺度桥接程序的方案(从左到右):杆材料数据集用于使用DDCM表征八隅体桁架单元的响应,这些RVE模拟产生线性弹性常数和非线性材料响应数据集,用于使用d-精化对建筑材料的立方体样本进行宏观模拟。
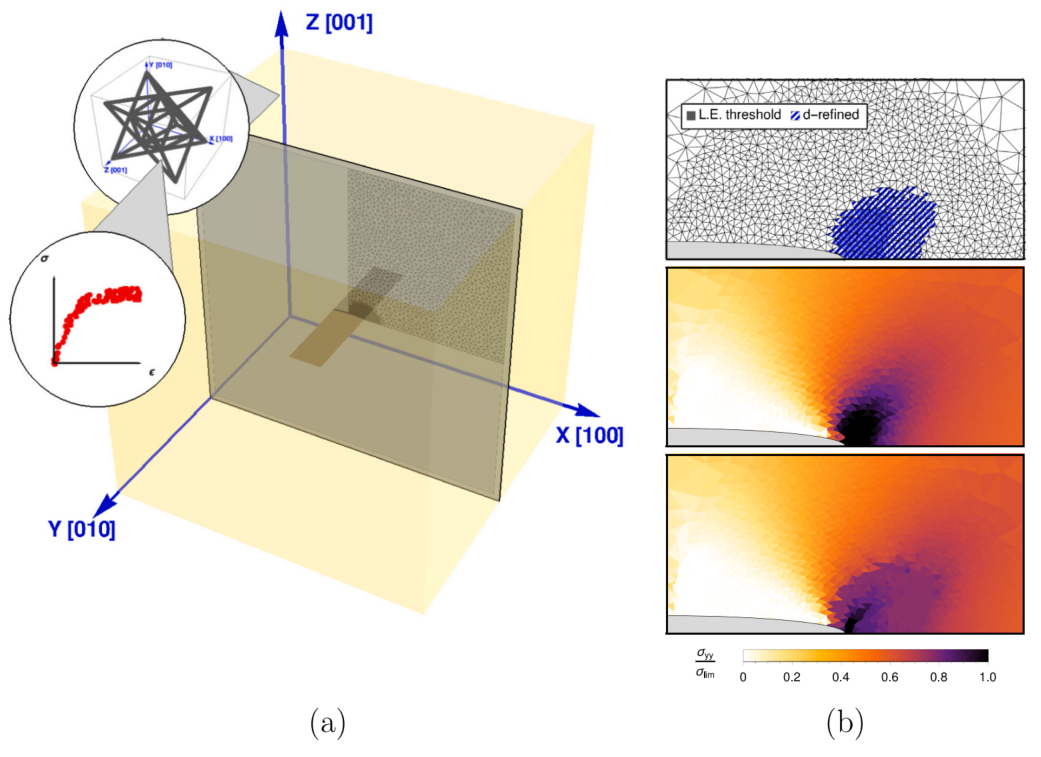
图:使用d-细化的宏观模拟,使用DDCM的RVE探测生成的数据。
文四:

数据驱动计算力学中的自适应目标数据采样
摘要:
数据驱动(DD)计算是计算力学的一个新兴领域,其动机是实验测量的最新技术进步、高预测性计算模型的发展、数据存储和数据处理的进步,这些都使我们能够从物质数据稀缺时代过渡到物质数据丰富时代。DD模拟的预测能力取决于材料数据集的质量,即其对给定力学问题的相空间中的所有应变-应力状态进行密切采样的能力。在这项研究中,我们开发了一种通过迭代展开来提高现有材料数据集质量的方法。利用DD范式处理的问题作为距离最小化问题的公式,我们在相空间中识别出数据覆盖率低的区域,并通过额外的实验或较低规模的模拟来针对它们。DD解决方案通知附加实验,使得它们可以提供给定应用的相空间的更好覆盖。我们首先通过线弹性圆柱在三轴压缩下的DD有限元模拟来说明该方法的收敛性。然后在具有复杂历史相关行为的Hostun砂样品上进行相同的数值实验。数据采样采用水平集离散元法(LS-DEM)计算代表该颗粒材料的晶胞,并采用所提出的方法确定的加载路径。研究表明,这种针对特定应用量身定制的数据集的自适应扩展可以实现收敛和准确的DD预测,而无需使用具有潜在冗余或低质量数据的大型数据库的计算成本。
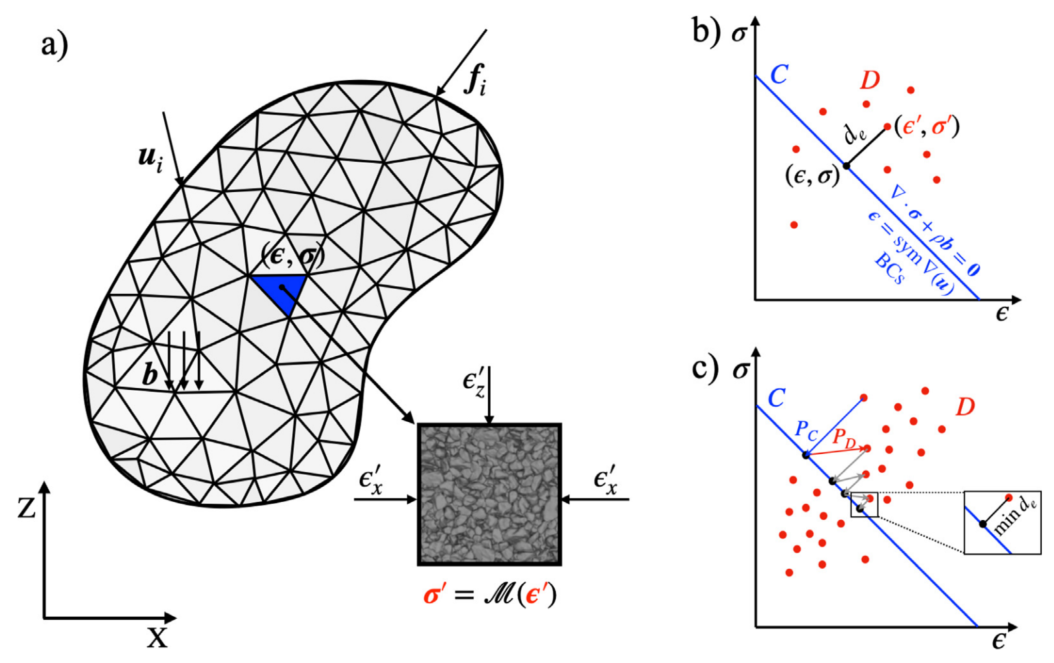
图:数据驱动方法概述。

图:数据集中材料历史的基于能量的参数化;可以从当前状态访问的材料应变-应力状态是那些符合热力学定律的状态。

图:自适应目标导向数据采样的典型迭代示例。
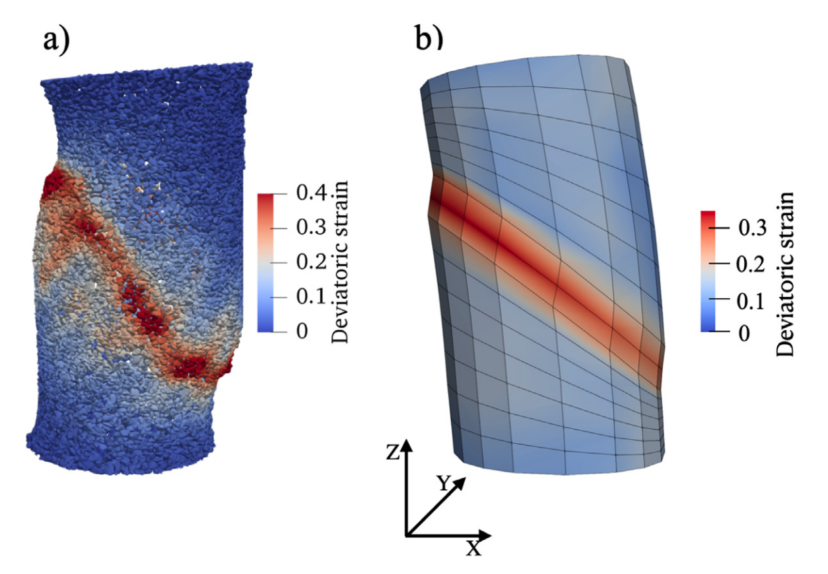
图:(a) 用LS-DEM模拟的非弹性三轴压缩圆柱体中剪切带的形成,以及(b)相应数据驱动模拟中圆柱体和剪切带形成的有限元离散化。

图:在非弹性圆柱体的初始DD模拟中穿过的覆盖不良单元的力学路径的聚类。
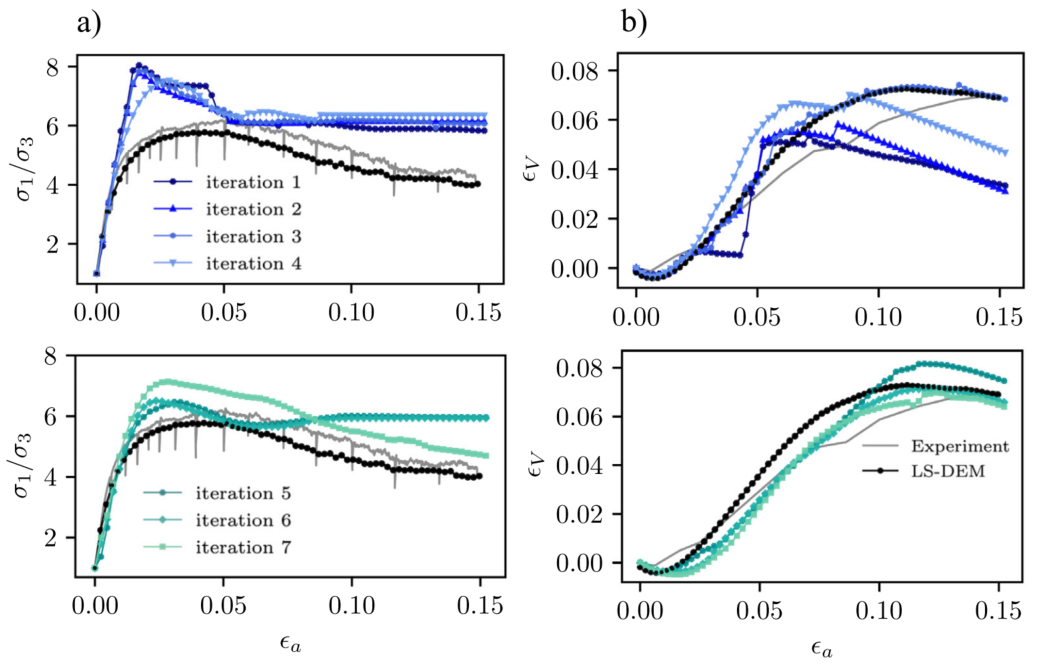
图:非弹性圆柱体宏观行为的数据驱动力学解,在连续迭代时;(a) 应力比与轴向应变和(b)体积应变与轴向应变。
文五:

数据驱动的非局部力学:发现材料的内部长度尺度
摘要:
非局部效应渗透到大多数微结构材料中,包括颗粒介质、金属和泡沫。自宇宙学家的开创性工作以来,对具有明确内部长度尺度的预测性非局部力学理论的探索已经进行了一个多世纪。我们在这里提出了一种新的材料行为非局部分析框架,它绕过了定义任何内部长度尺度的需要。这是通过将力学中最初为简单连续体引入的数据驱动范式扩展到广义连续体来实现的。该问题直接在材料数据集上公式化,该数据集由高阶运动学及其共轭动力学组成,这些运动学是从实验中确定的或从低阶计算中推断的。微极连续体的情况被用作引入框架的载体,该框架也可以适用于应变梯度和微形态介质。介绍了两个应用:带孔的微电极弹性板,用于证明该方法的收敛性;以及石英砂三轴压缩样品的剪切带问题,用于证明在复杂历史相关材料行为情况下该方法的适用性。
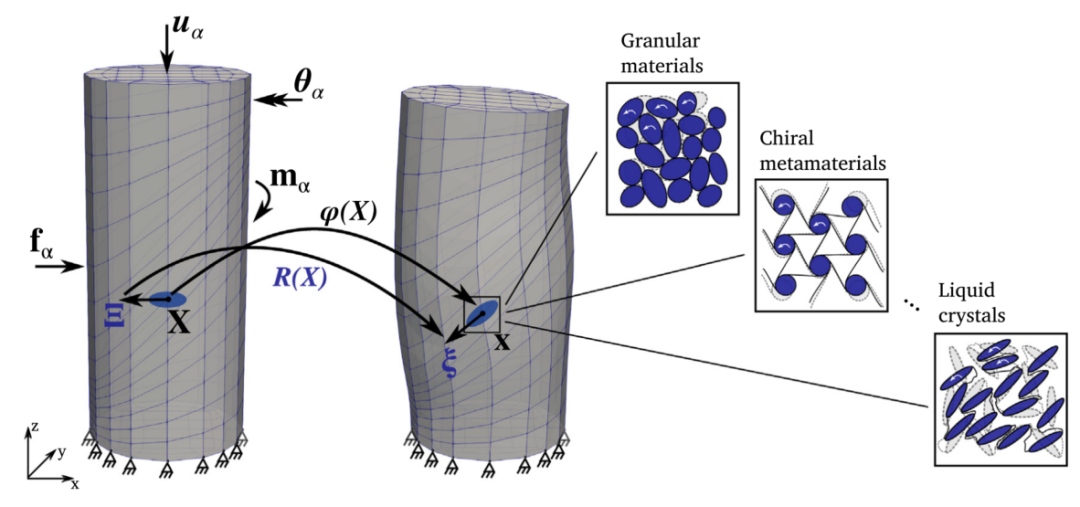
图:离散微极连续体的变形,以及适用于微极描述的微观结构类型。
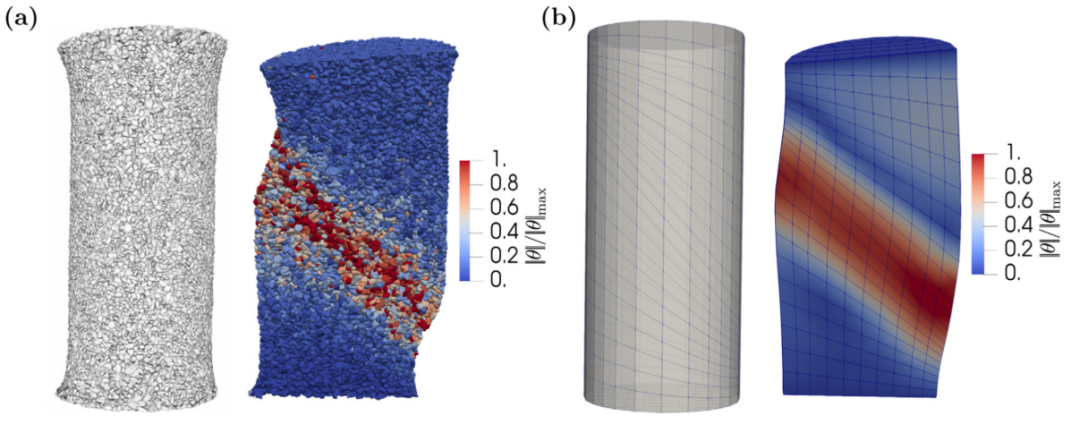
图:(a) Hostun砂的LS-DEM样本和(b)数据驱动有限元模型。两者都显示了未变形的圆柱形配置(左)和变形的局部横截面(右),具有归一化旋转幅度的轮廓。
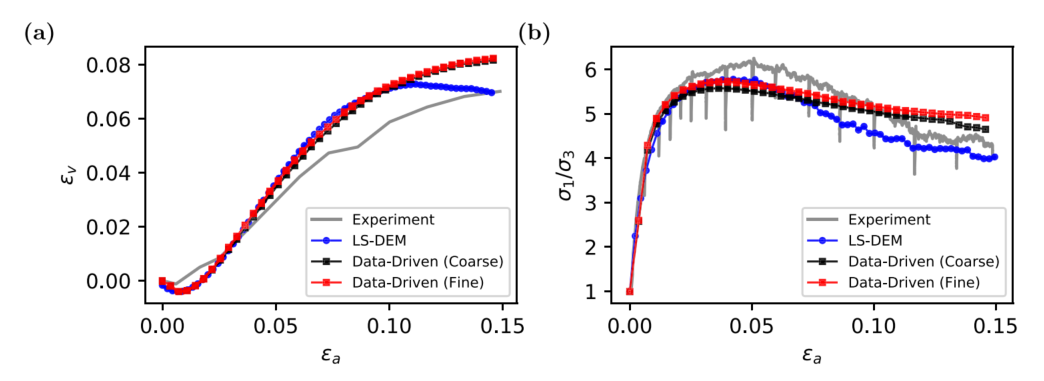
图:实验、LS-DEM模拟和数据驱动预测在(a)轴向应变与体积应变以及(b)轴向应变和主应力比方面的比较。
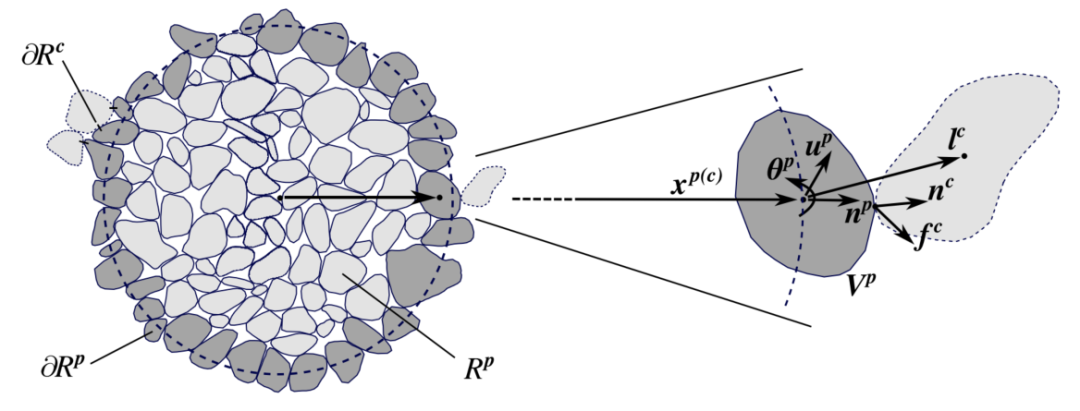
图:颗粒组件的代表性体积单元




