为什么基于两相流模型的滑动轴承流动特性研究,效果更好?
在国家基础工业领域内,燃气轮机、汽轮机、柴油机、汽油机、电机等各类旋转机械被广泛应用于航空航天、电力、汽车、机械、石油化工等各个关系到国民经济发展的行业中。
而轴承作为各类旋转机械的重要环节,其运转状态会直接影响到旋转机械的工作性能。尤其是随着各类旋转机械向着高转速、高性能的方向发展,旋转机械转子的工作状况日益趋于复杂,在对旋转机械的性能进一步提高的同时,对轴承各方面性能的要求也相应上升。
目前在旋转机械中应用的轴承形式包括滑动轴承、滚动轴承、气浮轴承和磁悬浮轴承等。其中,滑动轴承由于形式简单、承载能力大、回转精度高、寿命长等优点,在各类旋转机械中应用最为普遍。
1886年,Reynolds基于一定的假设,通过忽略方程中惯性力、彻体力等相对小量,对连续性方程、Navier-Stokes方程进行了简化,从而得到了表示轴承内部油膜压力分布的微分方程,即Reynolds方程。 Reynolds根据滑动轴承中润滑流体的性质及其在薄层中的运动特点,在简化N-S方程时采用的假设,包括: - 润滑流体介质是不可压缩的牛顿流体,即剪切力正比于剪应变率。
- 流体润滑膜的厚度相对于它的宽度和长度是小量,因此可以不计流体膜的曲率,不记表面移动速度方向的改变。
- 润滑剂在固体界面无滑移现象,附着于固体界面的流体质点的速度与固体界面相同。
图1所示坐标系下,等温不可压缩状态下雷诺方程的一般形式为: 式中,h为油膜厚度, U为轴承转速,c为轴瓦与轴颈半径之差,e为偏心距,φ为相对于最大油膜厚度处的角度。 Reynolds方程描述了两个运动物体表面间的运动速度、物体表面几何形状、润滑油物性粘度以及油膜压力分布之间的关系。 长期以来,Reynolds方程作为滑动轴承研究的理论基础而存在,带动了流体润滑理论及轴承技术的诞生与发展。在很多模型的很多工况之下都获得了良好的模拟结果,但从根本上讲,Reynolds方程的基础是建立在一系列简化上面的,因此求解计算相对来说比较方便快捷,但不可避免会产生相应的误差。 当轴承的工作条件与假设出现较大偏差时,Reynolds方程便不再适用,需要根据具体情况对其进行修正。
随着计算流体力学(Computational Fluid Dynamics,CFD)的发展,通过CFD手段来研究分析滑动轴承流场特性也得到了广泛应用。 CFD技术具有适应性强、应用面广的优点。由于流动问题的控制方程一般是非线性的,自变量多,计算域的几何形状和边界条件复杂,很难求得解析解,只有用CFD方法才能有可能找出满足工程需要的数值解;而且,可以利用计算机进行数值试验,从而进行方案比较。另外,CFD方法不受物理模型和实验模型限制,有较多灵活性,容易模拟特殊尺寸、高温等真实条件和实验中只能接近无法达到的理想条件。 目前针对滑动轴承流场特性研究主要是采用单相方法来实现的,不考虑负压区油膜压力分布,采用负压置零的方法来实现。 但目前国内外大量实验结果表明,轴承油膜分布中存在气穴现象。轴承内油膜产生气穴的原因理论上主要存在两种解释: - 气体气穴:当油膜压强降至大气压以下时,周围环境溶解在润滑油中的气体逸出并形成气穴,气穴内的压力与环境压力相同,这种情况通常发生在轴承油膜与大气连通的条件下;
- 汽化气穴:当油膜压强降至润滑油的饱和压强时,部分润滑油发生相变,汽化成为油蒸汽并形成了气穴,气穴的压力为油的汽化压力。汽化气穴中包含液态润滑油、油蒸汽和气泡等成分,气穴内压力为常压。
大量的实验结果表明,负压区内油膜并非完全破裂,而是破裂成细条状,有时也会出现蕨类植物状式的气穴状,它不仅存在于油膜开扩区,也可能出现在收敛区内。实验结果表明,负压区内同时存在气体空穴和油蒸汽空穴。气体空穴开始为单个气泡, 然后越来越大, 直到空穴内气体的数量恒定甚至能迁移到高压区不破裂,因此空穴内的压力有大气压力的许多倍。高转速、大偏心率不仅会致使气穴出现,还会导致气穴气泡变大,持续时间增长。 针对轴承内油膜气穴组成的特点,国内外学者提出多种两相流的研究方法。两相流理论的引入使得轴承开扩区内的压力分布和物质组成都得到了合理的解释,同时也进一步接近实验结果。 本文采用雷诺方程、单相流、两相流三种不同研究方法对圆柱轴承流动特性进行了分析对比。
研究结果表明,单相流、多相流模型对于整个油膜收敛区内的压力分布基本相同,主要差别表现在负压区内。单相流模型负压区内油膜压力为零,两相流模型负压区内油汽混合存在,如图2所示。 如表1所示,三种模型求出的最大压力相差不大,最大相对偏差为1.6%,但是Reynolds方程和单相流模型求出的有效载荷却小于两相流模型,相对偏差达8%。这是因为单相流和Reynolds方程都不考虑负压区的油膜作用的影响,使得两种模型有效载荷的计算结果偏小。 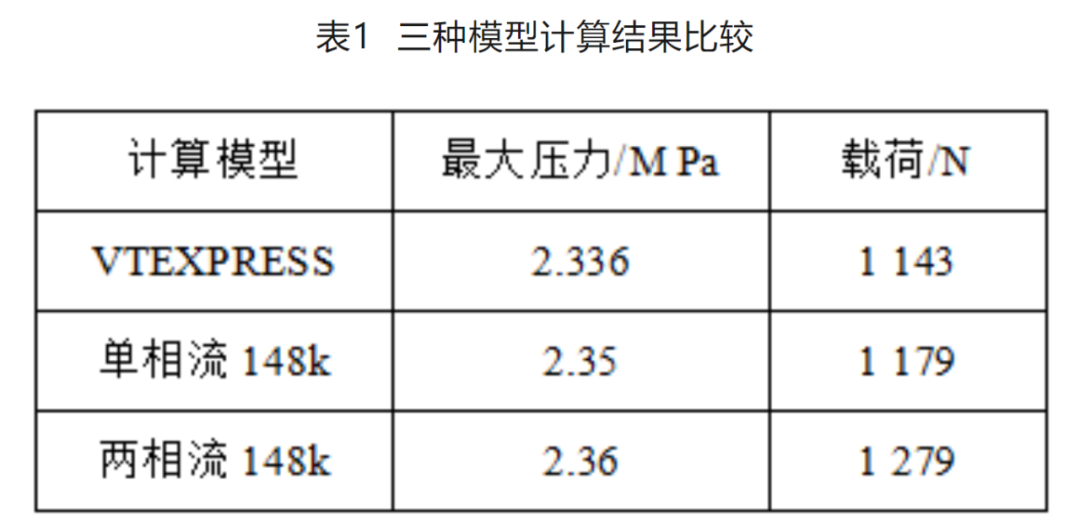
表2给出了三种模型在不同工况下计算结果与试验结果的比较。 Reynolds方程和单相流模型计算结果基本相同,但与实际载荷有较大偏差,相对偏差都在8%以上,最大达到近15%。相比之下,两相流模型求出的有效载荷更接近于实际值,相对偏差不到8%。 可以看出,在考虑两相流效应后,轴承承载力、油膜分布等更加符合实际情况,与实验结果吻合较好。 








