
如图所示,通过计算来评估公差标注的合理性:
45.6-10.15-15.25-20.3=-0.1 说明如果零件都加工处于上极限尺寸的情况下,会产生0.1mm的干涉,导致零件无法 正常装配,说明图面标注公差存在问题,需要优化。 再计按下偏差计算:
外框内径下极限尺寸:45.0
零件A下极限尺寸:9.85
零件B下极限尺寸:14.75
零件C下极限尺寸:19.7
计算:
45.0-9.85-14.75-19.7=0.7
说明如果零件加工都处在下偏差的情况下,会产生0.7mm的装配间隙。零件在实际加工过程中无法保证零件都处在下偏差。
再按零偏差计算:
外框内径基本尺寸:45.3
零件A基本尺寸:10
零件B基本尺寸:15
零件C基本尺寸:20
计算:
45.3-10-15-20=0.3
说明假定零件都处在基本尺寸的情况下,会产生0.3mm的装配间隙。同样在零件实际加工时无法保证零件尺寸没有偏差。
《机械工程文萃》编者补充:
按图纸中标准的尺寸公差加工后可能出现的间隙。
最大间隙:45.6-9.85-14.75-19.7= 1.3
最小间隙:45-10.15-15.25-20.3= -0.7
说明在零件都满足公差要求的情况下,可能出现1.3毫米的间隙,也可能出现0.7毫米的干涉,这两种极限情况都有可能不满足装配要求。
结合以上分析,三种极端情况下装配的间隙分别为:-0.1、+0.7、0.3,计算不良率:
要计算不良率,需要先计算有多少个零件处于不良状态。
假设有n个零件,其中x为零件处在上偏差时的零件数,y为零件处在下偏差,z为零件处在基本尺寸时的零件数,那么不良零件的数量为x+y+z。
不良率为:
(x+y+z) / n x 100%
根据题目所给条件,可以列出以下方程组:
x + y + z = n
x = n * ( - 0.1 / ( - 0.1 + 0.3 + 0.7) )
y = n * ( 0.7 / ( - 0.1 + 0.3 + 0.7) )
z = n * ( 0.3 / ( - 0.1 + 0.3 + 0.7) )
将上述方程组带入下面的公式中即可求出不良率:
( - 0.1 * n / ( - 0.1 + 0.3 + 0.7) ) + ( 0.7 * n / ( - 0.1 + 0.3 + 0.7) ) + ( 0.3 * n / ( - 0.1 + 0.3 + 0.7) ) / n x 100%
解得不良率为:15.24%。
结合上面的公差计算,产品在良产过程中会存在15.24%的不良率风险,所以需要调整装配公差。
1、尺寸链不完整,没有给出装配后允许的装配间隙(即尺寸链的闭环),没有分析比较的依据。 2、原文中存在很多概念错误。原文中“上公差”、“下公差”、“标准公差”实际因为“上极限尺寸”、“下极限尺寸”、“基本尺寸”,编者已作修改。 首先,零件加工的良率是呈正态分布的,即零件处于中间值的概率是最大的。本例中,零件处在基本尺寸的概率最大。 其次,计算不良率,即生产出的零件不合格品数量占总生产的零件数的比率,计算零件数量怎么要用到零件的间隙值?反而与最终的要求间隙值没有关系?况且尺寸都为基本尺寸时可能是合格的也参与不良率的计算,不合逻辑! 另外,原文作者连基本的概念都没有搞清楚(随时查一下资料或百度一下就可以的),严重怀疑其计算方法是臆想出来的。 4、也许是编者经验局限,欢迎读者在留言区文明发言探讨。后续本号会整理相关资料分享。 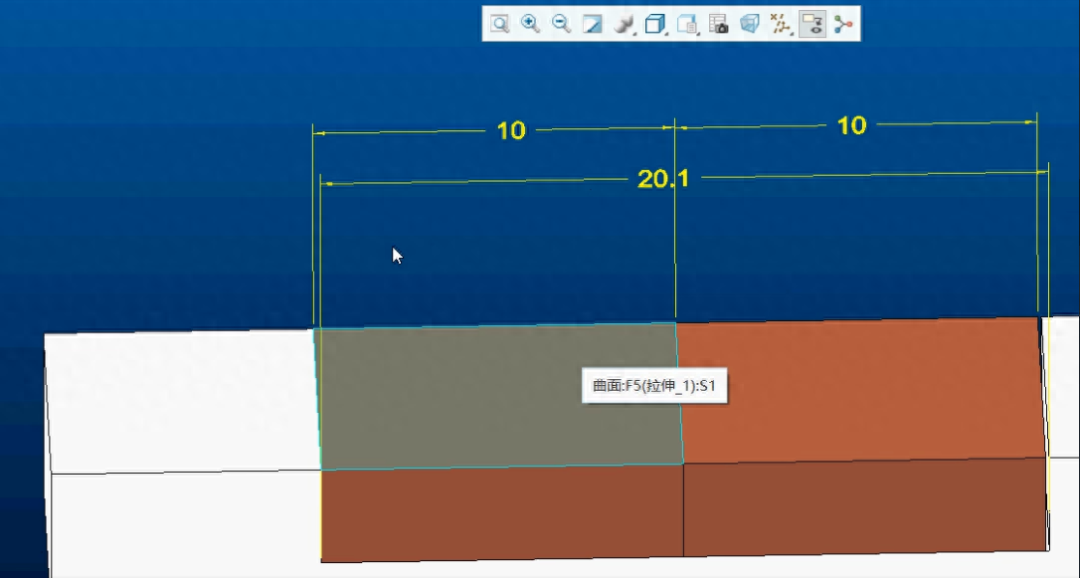
零件1公差为:10.00+0.00/-0.10;
零件2公差为:10.00+0.00/-0.10;
装配基准公差为:20.1+0.10/-0.00 。
这样公差链,无论是生产如何加工的话,只要是在公差范围以内,就会不存装配不良现象。
《机械工程文萃》编者点评:
1、同样没有明确给出最终的装配间隙值,所以是否合格没有明确的判断依据。
2、可以根据尺寸标注及给出的工程计算出最大间隙和最小间隙值。
最大间隙值:20.2-9.9-9.9=0.4
最小间隙值:20-10-10=0
可以得到的结论是装配间隙在0-0.4之间,并不能判断是否合格,不能说“不存在装配不良的现象”,甚至不能下结论说装配不存在干涉现象,因为还可能存在几何公差的问题。