想学Bouc-Wen滞回非线性优化仿真的看过来
本文摘要(由AI生成):
本文研究了基于Bouc-Wen滞回模型的仿真分析。首先定义了正弦波运动表达式,并通过变量方程和微分方程描述了仿真过程中的变量。接着,导入了测试数据并进行插值处理,以便与仿真结果进行比较。然后,设置了结果输出请求和输出时间域,并运行仿真提取结果。最后,通过参数优化分析了不同参数对滞回力-位移和滞回力-速度曲线的影响,并得到了优化后的参数和滞回力曲线。研究结果表明,优化后的参数能够减小滞回力仿真值与测试值之间的误差,提高仿真精度。
“任一时刻系统的恢复力不仅取决于该瞬时的激励和响应,还取决于其变形历程”,滞回非线性模型可以描述恢复力与位移间的这种记忆特征。在工程领域,具有滞回特性的非解析振动系统时有所见,其复杂的非线性动力学行为更是工业界诸多研究人员所关注的重点。那么,如何采用多体动力学软件来建立滞回非线性模型并确定其参数呢?
话不多说,快来跟着FunctionBay公司Technical Business Department [Senior manager] 资深技术Mr.Junewon (June), Seo学习采用RecurDyn建立Bouc-Wen滞回非线性模型吧。
首先来看一下RecurDyn中Bouc-Wen滞回模型的仿真结果:
通过RecurDyn后处理的模板化功能,能够极其方便地将所需要的仿真结果绘制出来,如下动图中四个视窗分别是:
Left upper : Displacement – Force curve
Right upper : Velocity – Force curve
Left lower : Time – Force curve
Right lower : Time – Force error curve
下面来详细说明基于RecurDyn进行Bouc-Wen滞回模型的建模仿真过程。
1. Bouc-Wen滞回模型原理图
下图所示为Bouc-Wen滞回模型,其中x,z为变量,A, beta, gamma, n, alpha, K, C是Bouc-Wen模型的相关参数。

2. 在RecurDyn中建立Bouc-Wen模型
2.1 创建Body

在RecurDyn建立3个Body,位置如上图,分别将其命名为Base、Action和Z_dummy。
2.2 创建Joint
在Base与大地Ground之间建立固定副Fix Joint;
在Action与Base之间、Z_dummy与Ground之间分别建立平动副Translational Joint.
2.3建立Force
在Base与Action之间建立平动力Translational Force.
2.4定义参数化值
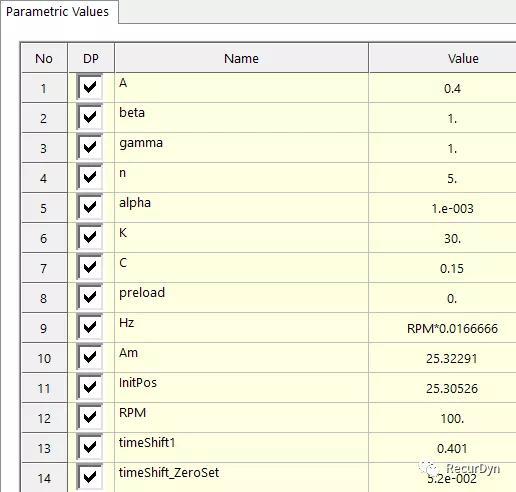
Bouc-wen model 5 parameters : A / Beta /Gamma / N / Alpha§Arbitrarily defined the parameter
K / C also defined the arbitrarilyparameter
Am : Sine wave amplitude
InitPos :Initial position of sine wave
RPM : RPM of sine wave
timeShift1, timeShift_ZeroSet :time-shifting to zero values
2.5 定义Expression及Motion
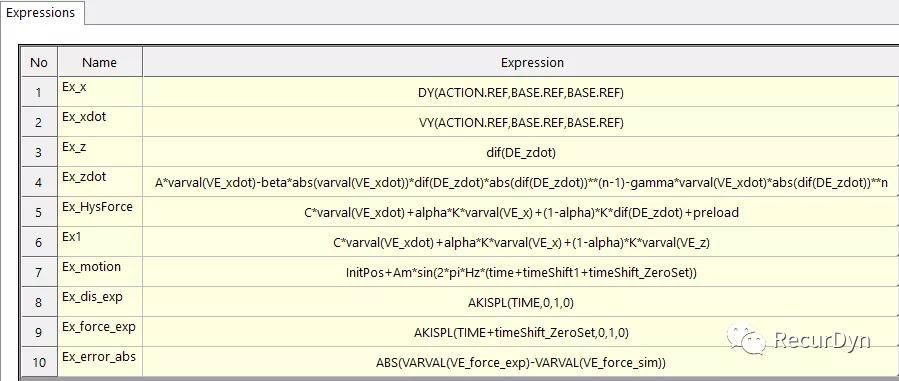
Sine wave motion
Action与Base之间Displacement驱动采用如下Sine wave motion表达式:
InitPos+Am*sin(2*pi*Hz*(time+timeShift1+timeShift_ZeroSet))
对于[1.6Hz、25mm],以时间time为变量的Expression可描述为 :
25.30526+25.32291*sin(2*pi*1.6*(time+0.401+ 0.052))
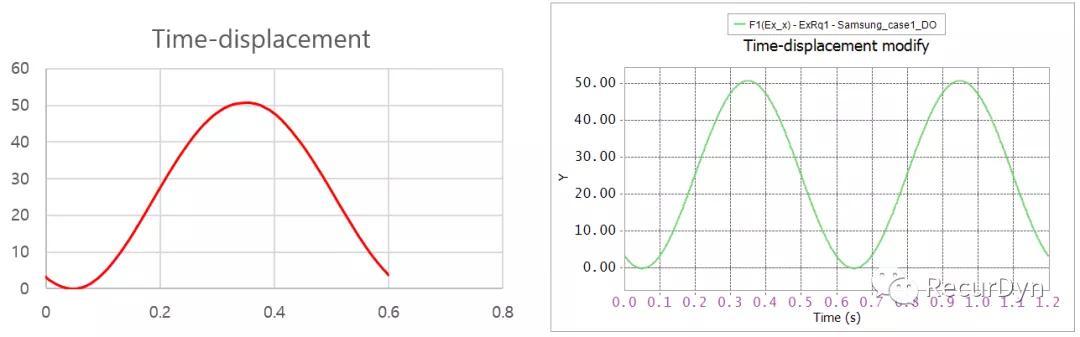
Varible Equation & Differential Equation
通过变量方程Variable Equation可以得到仿真过程的相应变量。

其中,VE_x表示Action与Base间的位移(如下图示的Y方向,即Bouc-Wen滞回模型原理图的x向位移):DY(ACTION.REF,BASE.REF,BASE.REF)

VE_xdot表示Action与Base间的速度(Bouc-Wen滞回模型原理图的x向):
VY(ACTION.REF,BASE.REF,BASE.REF)
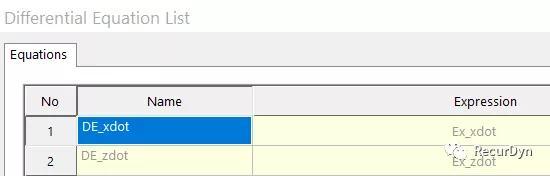
定义微分方程Differential Equation以便获得仿真过程变量的微分。
VE_zdot表示Z_dummy与Ground间的速度(Bouc-Wen滞回模型原理图的z向):
A*varval(VE_xdot)-beta*abs(varval(VE_xdot))*dif(DE_zdot)*abs(dif(DE_zdot))**(n-1)-gamma*varval(VE_xdot)*abs(dif(DE_zdot))**n
VE_z用于表示Z_dummy与Ground间的位移驱动(Bouc-Wen滞回模型原理图和z向):
dif(DE_zdot)
滞回力
Base和Action之间的平动力,即滞回力定义如下:
C*varval(VE_xdot)+alpha*K*varval(VE_x)+(1-alpha)*K*dif(DE_zdot)+preload
导入测试数据并插值处理
将测试得到的位移-时间曲线Sp_time_displacement导入,并进行插值处理:
AKISPL(TIME,0,Sp_time_displacement,0)

将测试得到的力-时间曲线Sp_time_force导入,并进行插值处理:
AKISPL(TIME+timeShift_ZeroSet,0,Sp_time_force,0)

滞回力仿真值与测试值的误差
ABS(VARVAL(VE_force_exp)-VARVAL(VE_force_sim))
3. 结果输出请求
采用Request将表达式的值进行请求输出:


4. 设置结果输出时间域

通过设置,仿真过程仅仅输出0.1s~0.9s的结果。
5. 运行仿真,提取结果
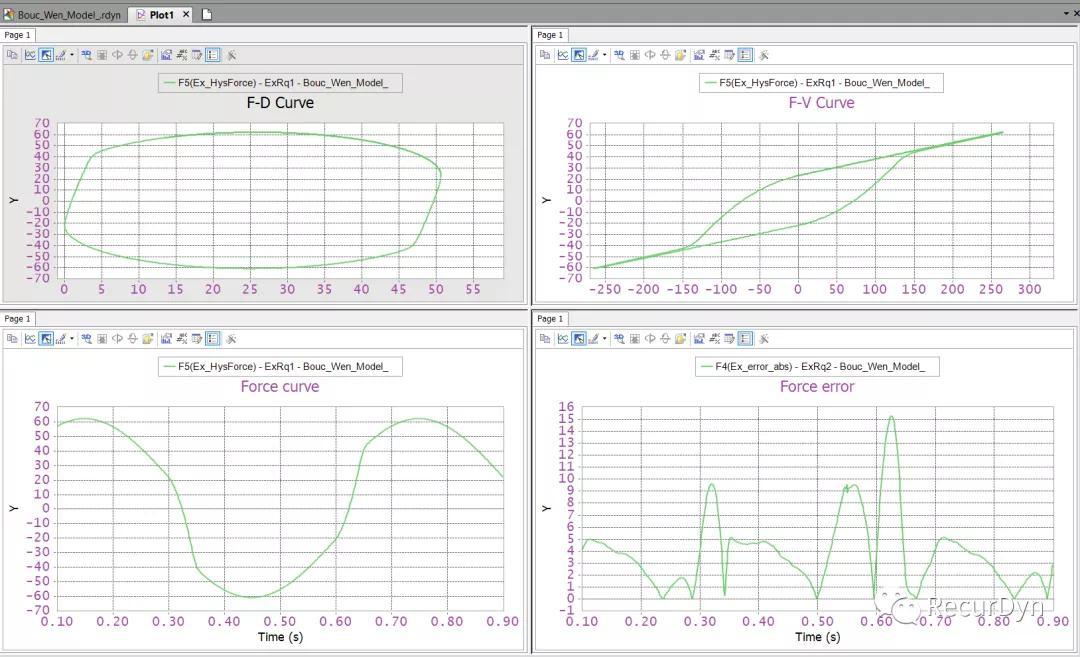
直接提交1s的动力学仿真,即可获得Bouc-Wen滞回模型的仿真结果。其中上面2图为滞回力-位移(F-D Curve)和滞回力-速度(F-V curve)曲线的横坐标分别为Action的位移和速度。
6. 参数优化
参数化研究
分别改变Bouc-Wen模型的参数,得到不同的滞回力-位移、滞回力-速度结果。
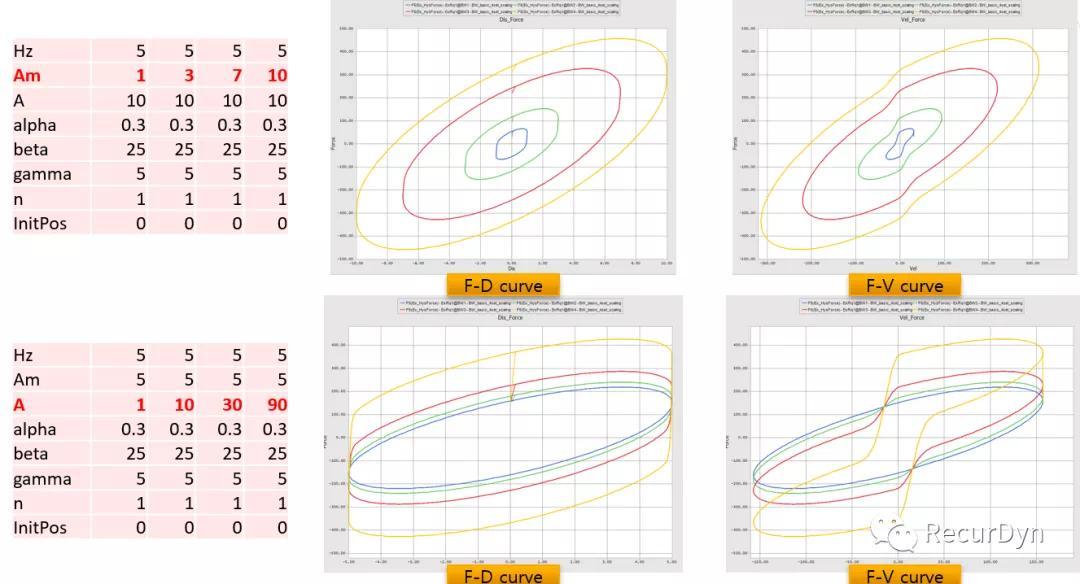

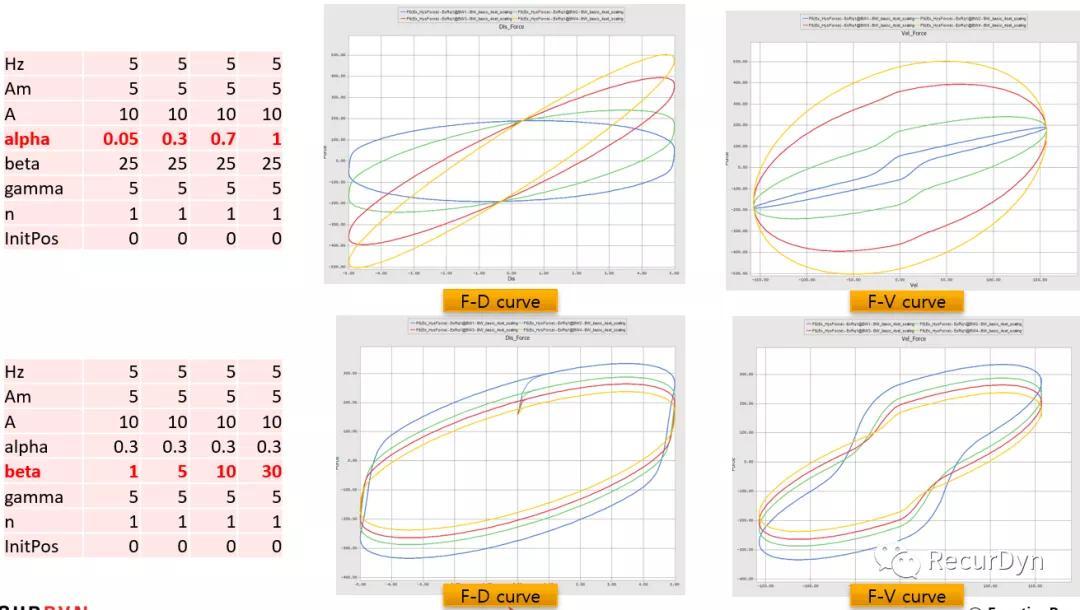
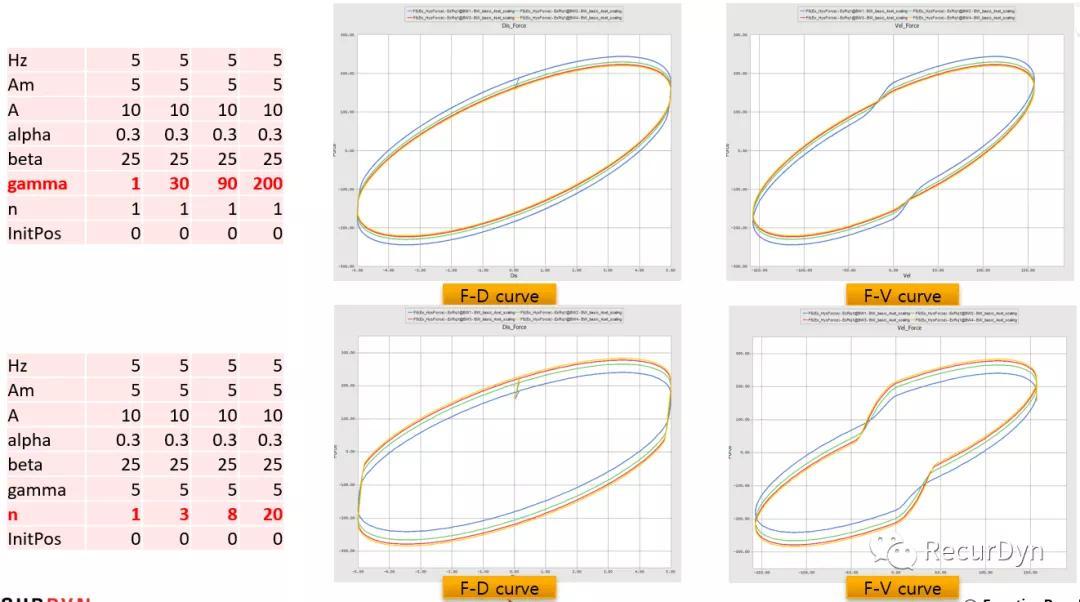
参数优化
将Bouc-Wen模型的参数作为设计变量,将滞回力仿真值与测试值误差的均方根RMS最小设置为目标,将滞回力仿真值与测试值误差最大值设置为14N(即14/60 * 100%=25% Error)进行优化分析.
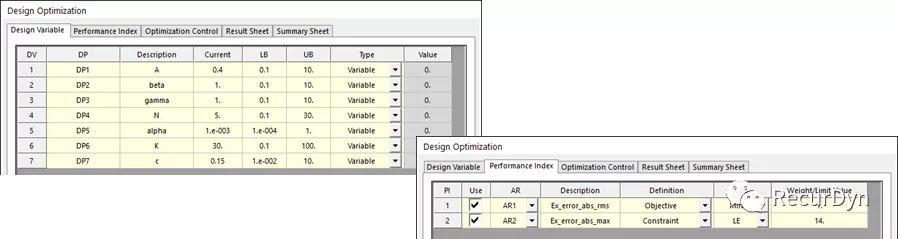
得到的优化参数及滞回力曲线如下:
Optimum | Initial | |
A | 0.783799 | 0.4 |
Beta | 2.281215 | 1 |
Gamma | 0.808271 | 1 |
N | 4.084292 | 5 |
alpha | 9.01E-04 | 1.00E-03 |
K | 30.7284 | 30 |
c | 0.138625 | 0.15 |






