湍流模拟|08 转角流修正
- 作者优秀
- 优秀教师/意见领袖/博士学历/特邀专家
- 平台推荐
- 内容稀缺
如第 3.4.3 节所述,涡粘模型需要经过特殊修正才能用来预测转角位置的二次流。
本节介绍转角流动修正(Corner Flow Correction,CFC)以及Wallin-Johansson模型(见第 3.3.3 节)中的 EARSM 项与不同 模型相结合,计算矩形流道和扩散器中的流动。对于这类流动问题,只有加入非线性项才能预测转角处的二次流。
因此,本节的主要目的是展示利用非线性湍流模型对转角处二次流预测的改进。GEKO 模型与转角流校正(CFC)和 EARSM 的组合显示了非线性效应。这些项对其他模型(如 SST 模型)的影响也与之类似。
1 方形管道中的发展流
描述二次流对主流影响的最简单的例子是方形管道中的发展流动。对于这种流动,线性涡粘模型无法预测进入转角的二次流。这种影响如图34所示。

在参考 DNS 数据[40]的条件下,基于平均摩擦速度 和通道宽度H条件下的雷诺数Re=1200,分别使用线性GEKO模型和非线性 GEKO-CFC 模型进行计算。计算在2.5D 模式下进行,其包含 3 个速度分量的动量方程,但假设它们的流向导数为零。流向压力梯度恒定以满足 DNS计算所对应的雷诺数。固体壁面采用无滑移壁面。
横截面上的流线显示,非线性 GEKO 模型可以预测二次流,而线性 GEKO 模型则不能(见图 34)。GEKO-1.00 模型、GEKO-1.75 模型和 WJ-BSL-EARSM 模型的流动结构几乎相同(未显示)。GEKO-EARSM 模型预测的沿对角线 (X=Y) 的流向速度分布与 DNS 数据相当吻合(见图 35)。右图显示横向流速计算结果似乎偏差较大。

2 矩形扩散器内的流动
矩形扩散器中的流动是一个比充分发展的通道流更具挑战性的测试案例,因为其涉及到各向异性湍流及导致流动分离的逆压力梯度。本节考虑了两种扩散器:对称的 DLR 扩散器 [41] 和非对称的 Stanford 扩散器 [42], [43],这两种扩散器中的流动对二次流预测高度敏感。
2.1 DLR-扩散器
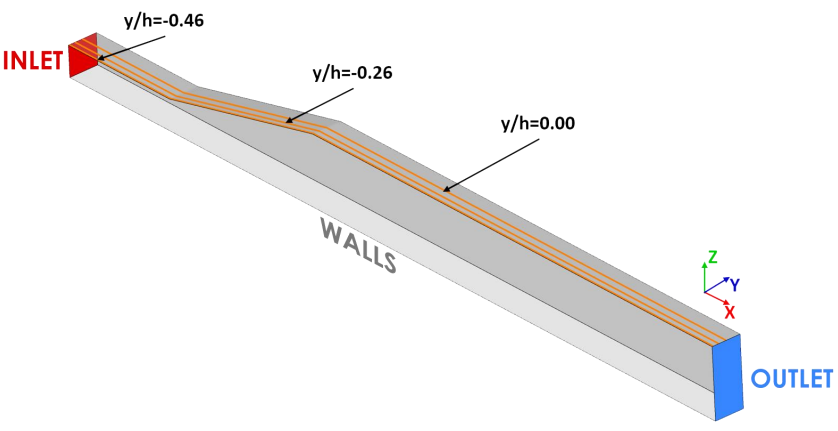
根据DLR的VicToria项目框架内的实验研究,对发生在端壁交界处的三维分离流动进行了模拟。在 CFD 研究中,考虑了膨胀比 ER = 2.0 的扩散器配置,几何结构如图 36 所示。计算域和边界条件如图 37 所示。计算域入口指定为速度 U=10 m/s、湍流强度Tu=1% 及湍流粘度比 TVR=1 的均匀流动。壁面采用无滑移条件,出口边界采用恒定压力。坐标系的原点位于平整壁面的中心线上,且与斜坡的起点位置重合。流动方向为X轴,Y 轴为跨度方向, Z 轴为通道的扩张方向。根据入口流速和横截面尺寸计算得到的雷诺数为 Re = 5.1e4。

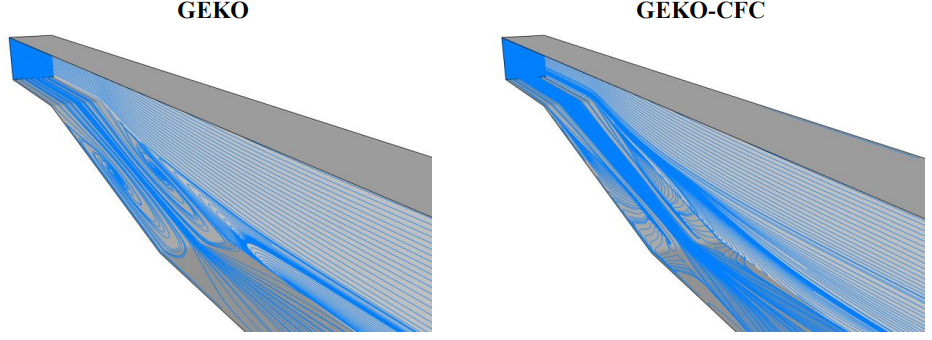
对于此案例,如图 38-39 所示,线性模型预测了从倾斜壁面转角处开始的两个再循环区。与此相反,非线性模型预测的二次流阻止了转角分离,并将再循环区推向倾斜壁面,而侧壁面上的流动实际上是连接在一起的。线性和非线性 GEKO 模型在倾斜壁面上的流线显示了流动拓扑结构的巨大差异,如图 38-39 所示。
预测得到的表面摩擦系数与实验数据(图40)的比较表明,使用非线性模型可改善转角(y/h=0.46)附近气流的预测,其中线性模型预测较大的转角分离。相比之下,扩散器中部(y/h=0)附近的流动对非线性效应不那么敏感。然而,所有的模型都预测在中部有一个附着的边界层,而在实验中,流动是分离。尽管线性和非线性模型的流动拓扑结构不同,但中段的压力分布(图41)与所有模型的实验数据一致。



2.2 Stanford扩散器
Cherry 等人[42]、[43] 在实验中研究的这种流动比上述流动更具挑战性。事实证明,在这种情况下流动分离对湍流建模的细节非常敏感。显然必须考虑法向应力的各向异性,以避免形成不正确的流动拓扑结构。
扩散器的几何形状如图 42 所示。扩散器顶部壁面倾斜 11.3°。为了实现不对称,其中一面侧壁倾斜了 2.56 度。计算中使用的坐标系如图 43 所示。坐标系在 X 方向上的原点位于扩散器的横截面上,该横截面与 Y 和 Z 方向上的直壁和斜壁的交点相对应,其位于扩散器直壁面形成的二面角的顶点上。
根据实验设置,将入口条件视为矩形管道中的充分发展流动,其雷诺数为 Re = 1e4。入口速度是通过对已形成的矩形管道流动的先导计算确定的,湍流模型与之后用于扩散器模拟的模型相同。计算使用了带或不带转角流动修正(CFC)的 GEKO 模型、GEKO-EARSM 模型和雷诺应力 GEKO 模型(GEKO-RSM)。


图 44 显示了线性 GEKO 模型、非线性 GEKO 模型及实验的三维流动拓扑图(注意,为直观起见这些图片旋转了 180°)。从图中可以看到,在实验中,流动分离主要发生在强烈倾斜的壁面上。线性 GEKO 模型预测在扩散器扩张位置会出现大量转角分离,分离发生在非倾斜的侧壁上。非线性模型减小了转角分离区域的大小,从而极大地改变了流动拓扑结构。在非线性模型中,分离主要发生在强烈倾斜的壁面上,这与实验的拓扑结构更为吻合。图 45 还显示了非线性对流动拓扑的影响,图中绘制了 X5 断面的流向速度等值线(蓝色表示负值)。非线性项改变了分离区的位置(从侧壁到斜壁)。所有非线性模型的计算结果都很接近。

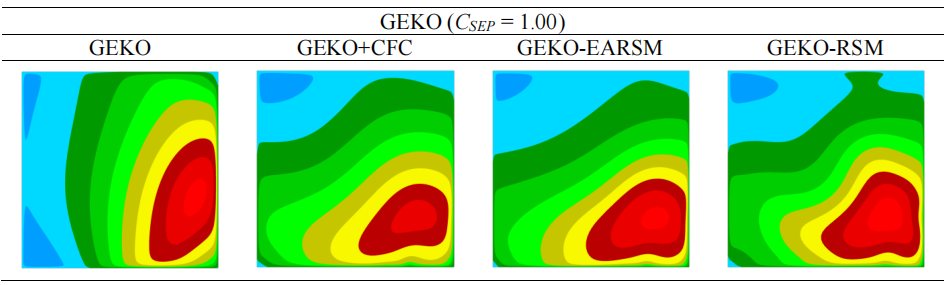
有趣的是,非线性模型的流动拓扑结构也取决于基线线性模型。图 46 显示,GEKO 模型中的 CSEP 值从 CSEP = 1.00 增加到 CSEP = 1.75 时,侧壁和斜壁都出现了分离。CSEP 值对压力系数预测的影响如图 47 所示。从图中可以看出,更激进的 CSEP 设置(更高的 CSEP)无法捕捉到整体压力分布。
测试表明,这种流动对建模细节极为敏感,因为不同的模型设置会得到不同的流动拓扑结构。CSEP = 1.75(通常用于空气动力流)的计算结果较差。这可能是由于模型预测的分离区较大。RANS 对这种区域的预测往往较差,因为分离线的小尺度脱落可能会主导再附着动力学。由于 RANS 未考虑此类影响,因此可能导致分离区过大。可以通过更保守的设置来减少误差,例如设置 CSEP = 1,它可以延迟分离,从而缩小分离区。虽然与数据的整体一致性更好,但这也有可能是误差抵消的结果。这个例子表明,看似简单的实验配置仍然会给 RANS 建模带来严峻挑战。


3 DLR F6飞机外流场
考虑在马赫数 Ma = 0.75 和雷诺数 Re = 3e6 的条件下,流经安装了发动机的 DLR F6 飞机构型的跨音速流(图 48)。为进行比较,选择了安装发动机的几何形状变体,攻角为1°,升力系数约为 0.5。计算使用 CFX 在 840 万网格的块状结构网格。有关在 ONERA 进行的测量的参考资料可从2nd AIAA CFD 阻力预测研讨会 (https://aiaa-dpw.larc.nasa.gov/Workshop2/workshop2.html) 上获得。

研讨会的主要挑战是预测未安装及安装发动机短舱的翼身之间的阻力差异。图 49 显示了使用 SST 模型得出的升力-阻力极值(不同点对应不同攻角)。可以看出,模拟结果表现不错。

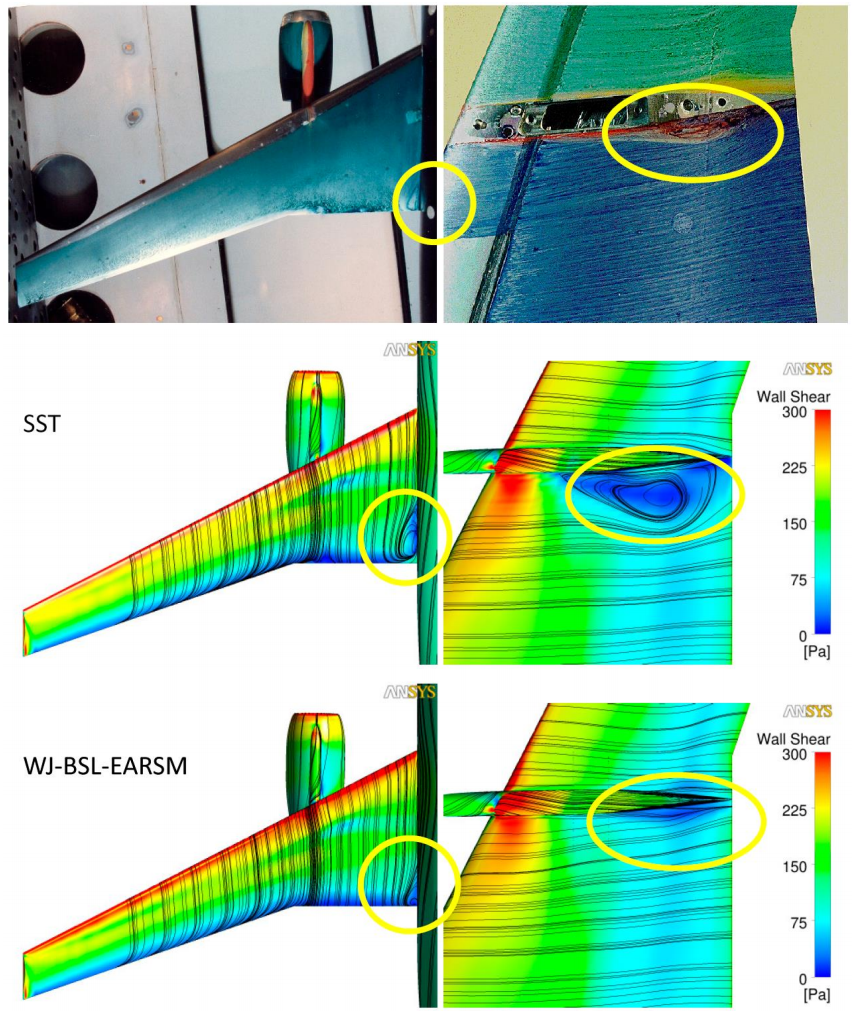
不过,在本节中,我们更感兴趣的是拐角处流动的预测以及非线性模型在这些区域的影响。如图 50 所示,由于 SST 模型缺乏对转角处二次流的预测能力,因此往往会高估转角分离区的大小。WJ-BSL-EARSM 模型改善了机翼上表面机翼-机身转角分离区的结果(图 50 左侧图片)。另一个转角分离区域位于发动机安装在机翼上的下翼面。SST 模型对该处的分离预测也进行了过高的估计。使用 WJ-BSL-EARSM 模型后,分离区面积大大减小,与实验结果趋于一致。
4 总结
非线性效应对转角处存在二次流的流动非常重要。线性涡粘模型无法 正确预测转角处的流动拓扑结构。对于存在压力梯度和分离的流动,这可能会导致对流动拓扑结构的错误预测。CFC 或 EARSM 等非线性模型可显著改善对此类流动的预测。
注:系列翻译自《Best Practice: RANS Turbulence Modelingin Ansys CFD》,作者F.R. Mentor,2022
”
(待续)




