应用相图的振动系统的定性分析方法

所谓振动,即物体在一定位置附近做来回往复的运动。单自由度的振动系统都可看成是振子,其中最简单的例子就是弹簧-质量系统,由一个忽略质量的弹簧和一个忽略体积的质点组成。其中质点作为振动的主体,弹簧提供振子的恢复力。
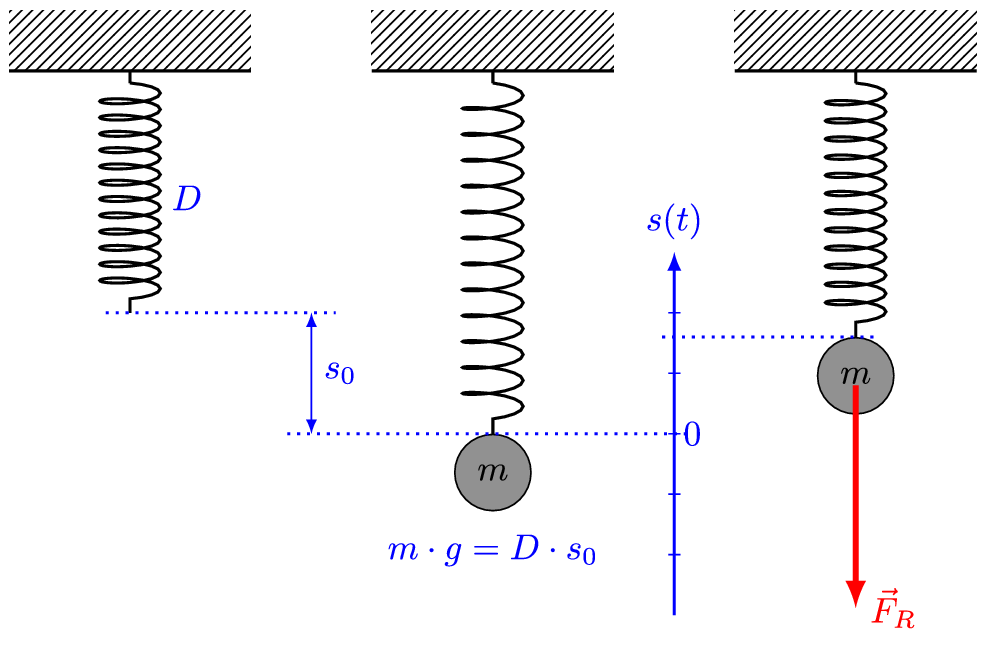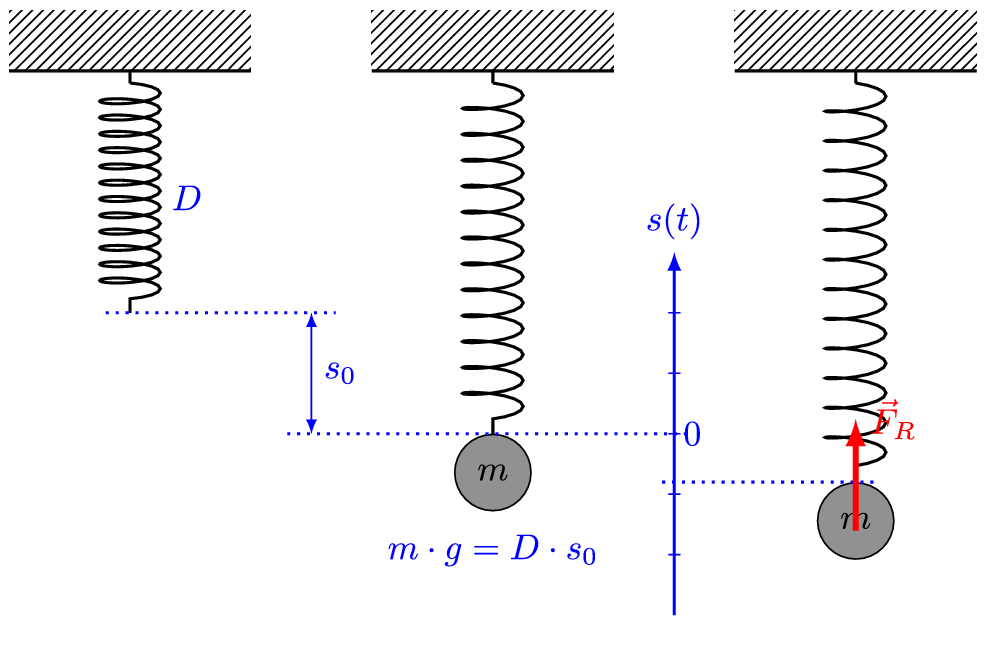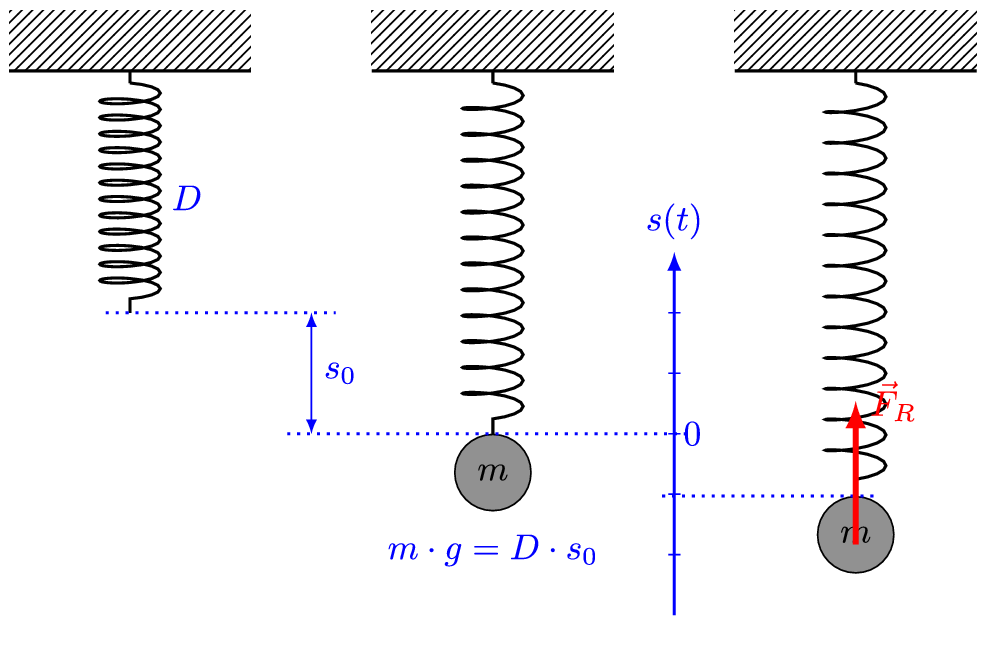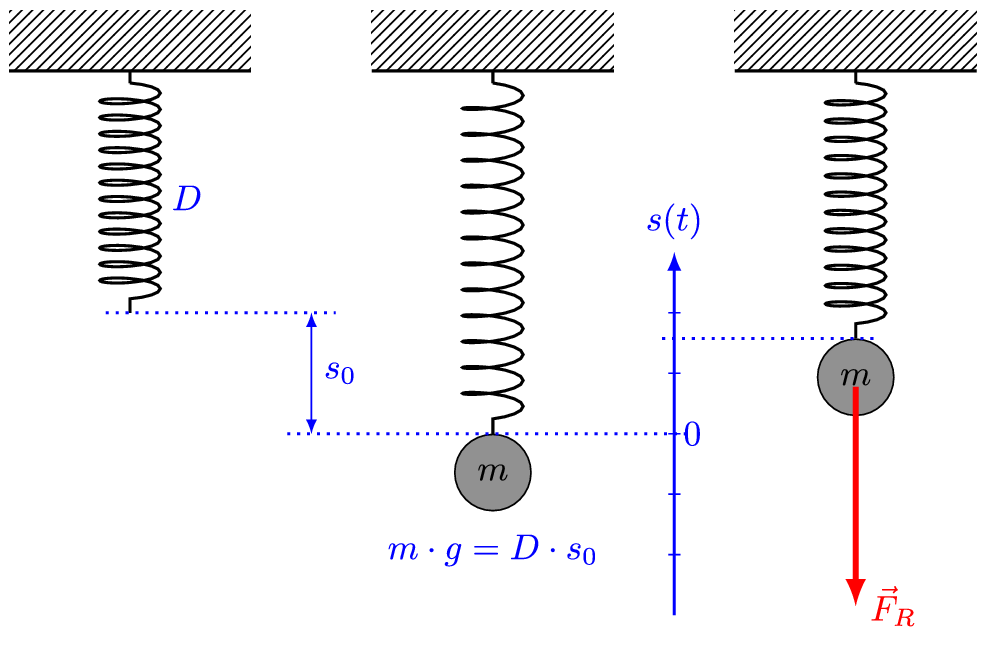
图中D代表弹簧弹性系数K,s0代表弹簧连接质点后的平衡伸长量,s代表质点相对于平衡位置的位移。
在物理课中,我们通常使用牛顿力学的方式建立运动方程,解出系统位移随时间变化的运动方程,以直观地观察系统的运动状态。如之前提到的弹簧振子中,其弹簧恢复力与质点相对于弹簧平衡点的位移x的关系由胡克定律指出:在弹性限度内,弹簧的弹性力F的大小和弹簧长度的变化x成正比:

结合牛顿第二定律,弹簧的作用力F与质点的加速度a成正比:
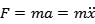
则可以得出弹簧振子的运动方程:
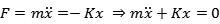
由于正弦函数和余弦函数的二阶导数都是其本身乘以一个系数:
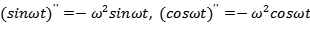
所以可以将这两个函数的线性组合设为运动方程的解:
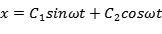
带入运动方程可以得到:

由于质点振动时位移x不恒为0,所以:
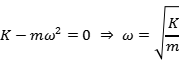
其中ω称为系统的固有频率,是由质点的质量m和弹簧的弹性系数K,这两个物理属性唯一确定的,不随外界条件而改变。
再利用三角函数中的辅助角公式,我们可以将运动方程的解写为正弦函数的形式:
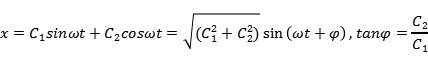
所以我们可以清晰地看出,弹簧-质量系统的振动曲线是一条正弦曲线,这种按正弦规律进行的往复振动称为简谐振动,是最常见的振动形式。
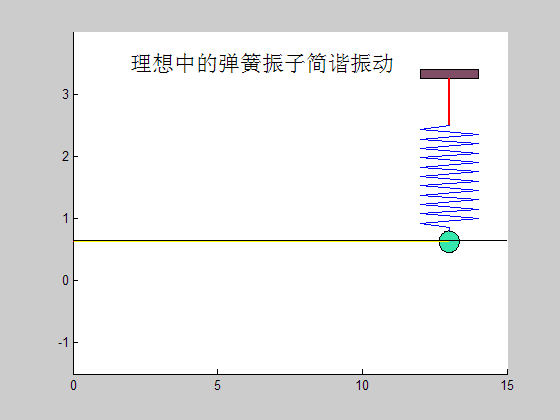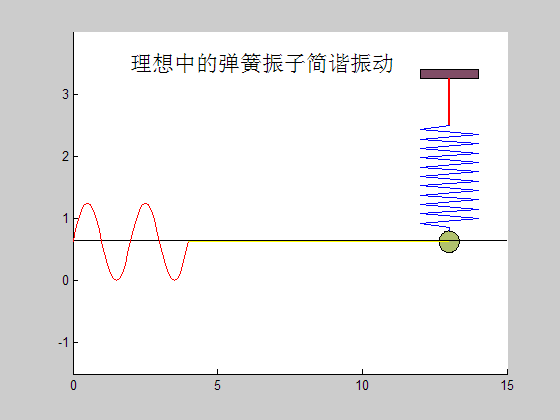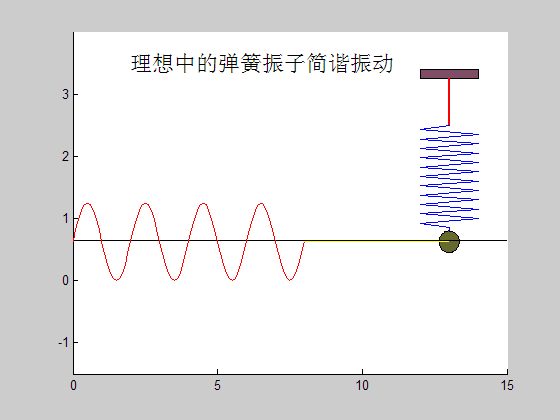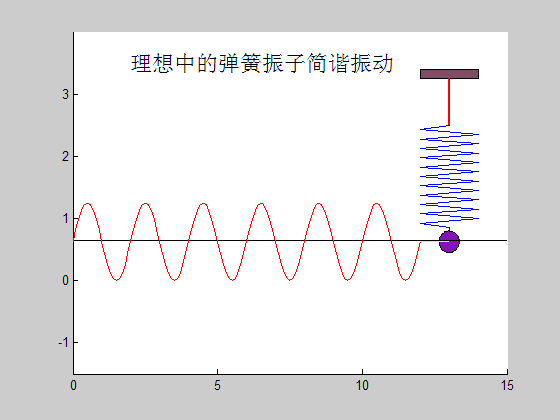
至此,我们得到了弹簧-质量系统振动的直观表现形式,但方程的解中还有两个系数C1,C2没有确定,当这两个系数确定时,系统的振动方程也便唯一确定。为了确定这两个系数,我们需要知道系统在t=0时刻的初始条件:
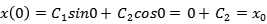
这个式子表明,质点的初始位移x0可以确定系数C2。为了确定C1,考虑到sin0=0和cos0=1,对x求一阶导即可将C2部分同上式一样变为0,即:
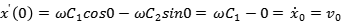
这个式子表明,质点的初始速度v0,可以确定系数C1。所以我们所需要的确定振子运动状态的两个量为质点的初始位移和初始速度(x0,v0)。对此加以推广可以知道,不只有0时刻的位移和速度可以确定两个系数,任意时刻t的质点位移和速度,都可以确定振子的运动状态。所以,质点的位移和速度是表达振子运动状态的两个变量,称为状态变量。
现在,我们得到了一组与传统的直观表示运动状态的(x,t)变量不同的新变量组(x,v)。若以x和v为直角坐标建立(x,v)平面,则称此平面为系统的相平面。在每个确定的时刻,质点有其唯一确定的位移x和速度v,这与相平面上的点一一对应,这些点称为相点。随着时间的推移,这些相点构成一条曲线,称为相轨迹。
相平面的原点是一个特殊的点,其表示质点的位移和速度都为0,所以其静止不动,对应系统的平衡状态。因此相图的原点也称为平衡点。因此,当弹簧-质量系统处于平衡状态静止时,其对应的运动图为一条直线,而对应的相图为一个点。
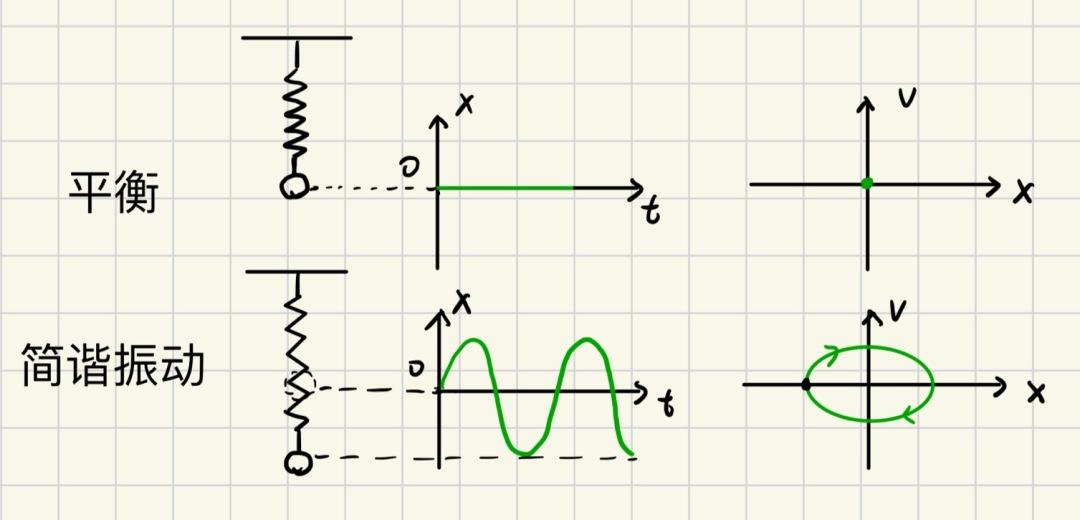
当振子在外界的扰动下开始运动时,相点就离开平衡点位置,改为沿平衡点附近的相轨迹移动。对于简谐运动,其运动方程为
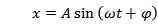
则
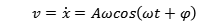
于是我们可以得到相平面的相轨迹方程:
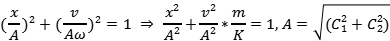
这是一个椭圆方程,椭圆的大小随着振幅的增大而增大,相同系统不同振幅的简谐运动对应的不同椭圆构成一个族,将相平面原点包围起来,此时相平面原点又可称为中心。这种相图表示稳定平衡状态附近的振动,如弹簧-质量系统运动的相图。
既然得到了稳定平衡状态下单自由度振子的运动相图,我们自然会思考,非稳定平衡状态下物体运动的相图又该如何呢?我们可以利用弹簧-质量系统的变体来分析。
在弹簧-质量系统中,质点偏离平衡位置时,恢复力与运动方向相反,使质点回到平衡位置。而非稳定平衡状态下,质点离开平衡位置后,所受到的力与运动方向相同,使质点更快地离开平衡位置。与弹簧-质量系统相比,相当于将弹簧的弹性系数K变成负值,于是相轨迹方程将变为:
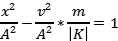
这是一个双曲线方程,因此不稳定的负刚度系统对应的相轨迹是双曲线族,相点只要稍稍偏离平衡点,就会沿着双曲线越来越快地无限远去。这种被双曲线围绕的原点称为鞍点。
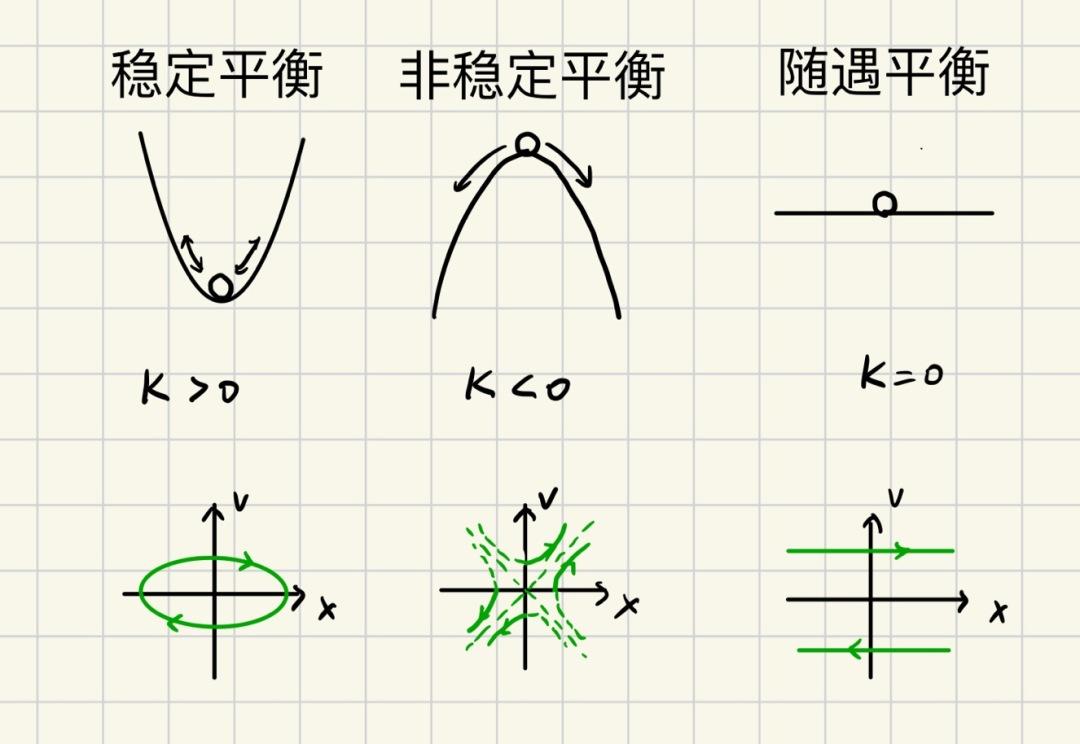
因此,运动的性质可以由相平面原点的类型反映出来,这种利用抽象的相轨迹的几何特征来判断实际物体的运动特征的方法,即为振动的定性分析方法。




