仿真笔记——有限元几何非线性问题详解,及ANSYS处理技巧
什么是非线性
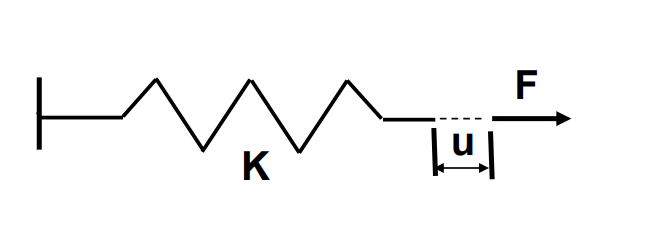
借助胡克定律可以理解线性问题,如一个弹簧单元遵守如下的方程:
F=K×u

结构的变形与受力始终是线性关系,结构的刚度在整个计算过程中不发生变化。但是在非线性问题中,结构的刚度不是一成不变的,它可以随着一些原因发生改变,如下图所示,其中Kt称为切向刚度。

1. 几何结构发生大变形,从而导致刚度不再符合线性关系,这种情况属于几何非线性;
2. 当材料的应变超过了弹性极限,即应力-应变曲线不再服从线性分布,这种情况属于材料的非线性;
3. 结构的状态变化导致的非线性,这种情况属于接触非线性;
由此可见,有限元分析中的非线性问题可以分为3类,几何非线性,材料非线性与状态/接触非线性,本文主要对几何非线性问题进行详细描述。在介绍几何非线性之前,先了解一下线性问题中的小变形假设,这是弹性力学以及线弹性有限元分析的前提条件。在弹性力学中,小变形假设指物体在外力作用下产生的变形与其本身几何尺寸相比很小,可以不考虑因变形而引起的尺寸变化。这样就可以用变形以前的几何尺寸来建立各种方程,同时应变的二阶分量可以忽略不计,仅为线性表达式。但是,在实际工程中存在很多情况都不符合这种小变形假设,此时应该用变形后的几何尺寸来建立方程,几何关系中包含了多次项,这就出现了非线性问题。几何非线性是指结构或部件在发生偏转时,由于几何形状变化而产生的非线性,即刚度K是位移u的函数。刚度变化是由于形状变化或材料旋转,主要表现为大应变,大位移,应力刚化和旋转软化。1. 大应变:一个结构的总刚度依赖于单元的方向和刚度,如果一个单元的形状发生变化则它的刚度也发生变化,如果这个单元的方向改变,则局部刚度到全局刚度的转换关系也会发生改变。小变形假定这种刚度的改变无足轻重,相反,大应变分析要考虑单元的形状和方向改变导致的刚度变化。这种效应可通过打开“大变形”进行激活,相应的工程案例有橡胶,海绵的受力变形,金属的塑性成形等。
大位移:也可以称为“大旋转”或“小应变”,在大位移分析中假定单元的转动可以任意大,但应变是小的,没有大的形状改变。在所有梁单元和大多数壳单元中,这个特性是可用的,也是通过打开“大变形”进行激活,相应的工程案例有承受压力的薄壁容器,鱼竿等细长的悬臂梁结构端部承受竖直向下的载荷等。应力刚化:内应力和横向刚度之间的联系通称为应力刚化。应力刚化是指构件在无应力状态和有应力状态下的刚度变化,在有应力状态下,构件某方向的刚度显著增大。比如悬索桥主缆或斜拉桥的拉索在未加轴向拉力时,其横向刚度几乎为零;但是在受到很大拉力作用的时候,其横向刚度显著变大,这就是应力刚化效应。在“大变形”中也包含了应力刚化效应,相应的工程案例有悬索,吉他等弦状结构等弦状物体的分析。
旋转软化:动态质量效应调整软化旋转物体的刚度矩阵,在小位移分析中,这种调整近似于由于大的环形运动而导致几何形状发生改变的效应。但是要注意,旋转软化不和其他的非线性效应一起使用,只有在进行指定转速的预应力模态分析时,旋转软化才可被激活,相应的工程案例有陀螺的模态分析等。几何非线性问题在工程中的失效形式主要表现为:失稳。那么在有限元分析中,要如何应对几何非线性问题,以及该类分析与线性分析在哪方面存在不同呢?在Ansys Workbench中,相比于线性分析,对于几何非线性问题需要做如下处理:- 在几何模型处,需要确定本次分析使用的积分方式(完全积分或缩减积分),一般默认即可。
将单元控制改为"手动",点击模型树中的零件,可选择积分方式。
- 若预感网格会出现大应变,在分析复杂模型时可选择"非线性机械",划分出的网格质量会高于默认;
- 网格质量检查可选择"强力机械",使网格检查更为严格,提高网格质量;
注:网格设置在几何非线性分析中不是必须的,可根据实际情况进行调整。- 在不考虑材料非线性的情况下,与线性问题的设置保持一致即可。
Ansys使用线性求解器进行非线性求解,将载荷分为一系列增量形式并逐渐施加载荷,同时在每 一载荷增量结束时调整刚度矩阵—牛顿法。因此,需要设置载荷增量(即载荷子步),求解控制与收敛准则。- 步控制:开启自动时步,分别设置初始子步,最大子步和最小子步
例:初始20,最小10,最大100,则第一步施加总载荷的1/20,之后每一步施加总载荷的1/10~1/100,当施加了全部载荷并收敛时,完成计算;1)求解器类型:直接法和迭代法,直接法即稀疏矩阵求解器,稳定性更好,建议用于非线性更强和具有非连续性单元(壳单元和梁单元)的模型。迭代法(PCG)求解器效率更高,建议用于以线弹性为主的大 体积实体模型。求解非线性问题时,可选用直接法,或程序控制;2)大变形:非线性分析中必须要开启大变形,大变形是一种算法,它考虑了结构变形后的刚度矩阵重建。一般情况下,对于普通精度要求的问题,变形超过5%或转角超过10°时,建议打开大变形开关;
1)牛顿法:用于指定求解过程中刚度矩阵的更新频率,完全法即每次迭代都更新刚度矩阵,非对称法与完全法一样每次更新刚度矩阵,不同的是它还生成非对称矩阵,适用于非线性很强的情况,比如摩擦系数>0.15。非对称也将比完全法消耗更多的时间和资源。如果使用完全法收敛困难,可以修改为非对称将更有利于收敛。2)收敛准则:主要使用力收敛准则(指残余力收敛),位移收敛用于相对检测,当模型存在转动时,需要力矩和旋转收敛。因此分析实体或2D单元时,使用力+位移收敛,分析梁或壳单元时,使用力+位移+力矩收敛。一般情况下,均使用程序控制即可,当计算难以收敛时,可仅保留力收敛,关闭其他;4)稳定性:用于处理屈曲问题和局部屈服;
- 重启动控制:中断求解,修改已有参数的设置,从保存点继续开始求解;
求解方案信息
如下所示,Newton-Raphson残余设为5,计算完成后可查看最后5次迭代是的残余力计算结果,若计算结果未收敛,可通过残余力的云图找到出现问题的位置,进行相应修改。在Ansys Workbench中,牛顿法的计算原理如下图所示,第一次迭代,施加总载荷Fa。得到位移结果x1。根据位移,算出内力F1 。如果Fa≠F1,系统不平衡。因此,根据当前的条件,计算新的刚度矩阵(虚线的斜率)。Fa-F1的值称为不平衡力或残余力。残余力达到足够小时,求解收敛。因此,需要在1个载荷步内设置若干子步,逐级子步加载最终达到收敛。
本文来源CSDN博主「YORUNOKUNI」