02 第一个案例从模型管理开始——HyperMesh速通2
俗话说没吃过猪肉先看看猪跑,虽然现在我们还不会使用HM进行前处理,但是并不妨碍我们用它来管理一个模型,并在此过程中熟悉HM的模型管理逻辑。本例是一个多段汽车保险杠模型。
1 打开与导入模型
这一节主要为了熟悉打开与导入操作。
首先打开HM软件,选择OptiStruct环境。
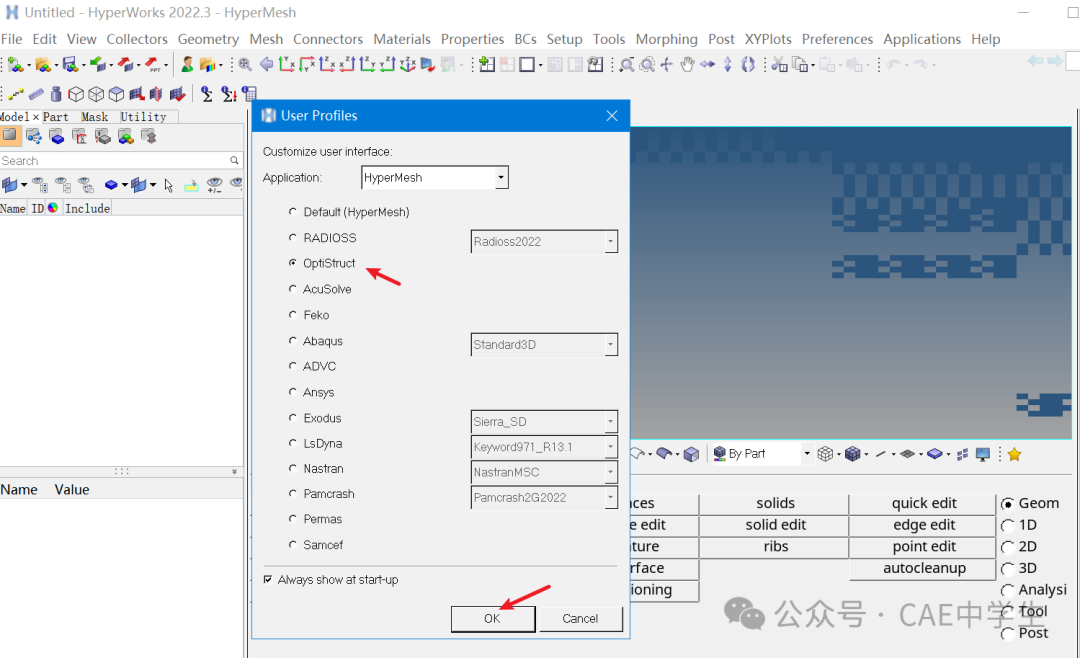
Step1 打开hm文件
通过Open Model或者File——Open——Model案例打开文件bumper_cen_mid1.hm文件。hm是HyperMesh的专用格式,可以保存几何、模型、材料、接触、载荷与约束等所有前处理数据。
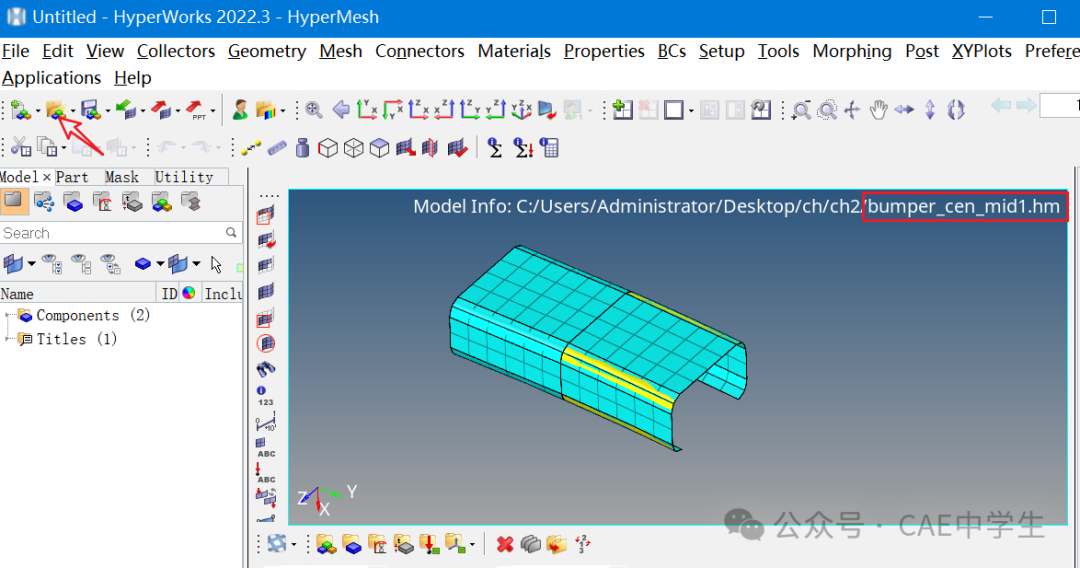
Step2 导入hm文件
通过Impot或者File——Import——Model导入bumper_cen.hm。这里使用导入是在原模型上增加模型,每个模型都会按自身坐标对齐。
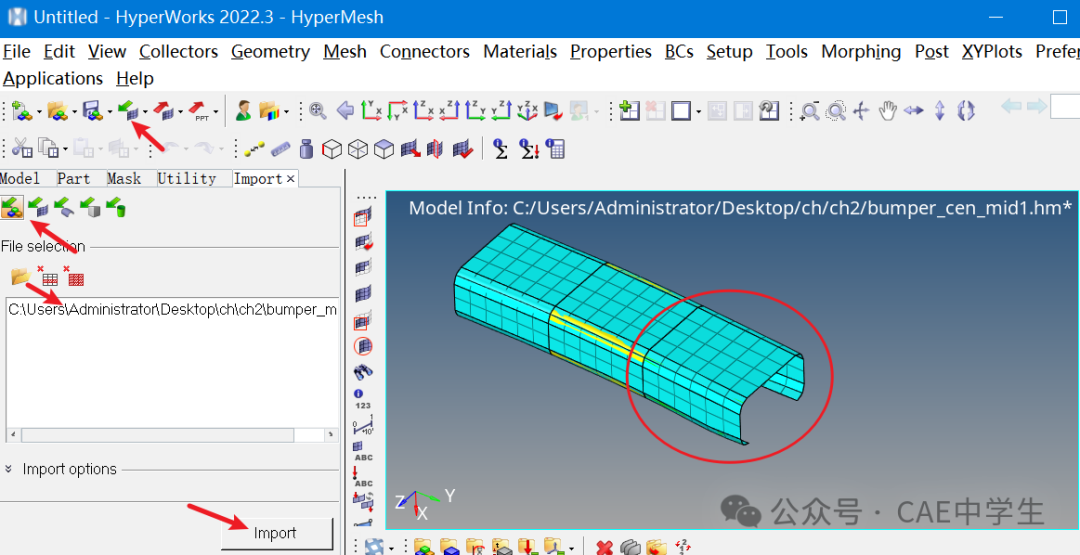
在Model结构树中的Components中,可以看到有三个组件,分别点击每个组件的几何或网格,可以发现三个组件中即有几何,也有网格。

Step3 导入几何模型文件
通过Impot——Geomery或者File——Import——Geomery导入bumper_end.iges。

通过Model组件可以看到此几何包括两个组件。

Step4 导入fem文件
通过Impot——Solver Deck或者File——Import——Solver Deck导入bumper_end_rgd.fem,文件类型选择OptiStruct,关闭警告。
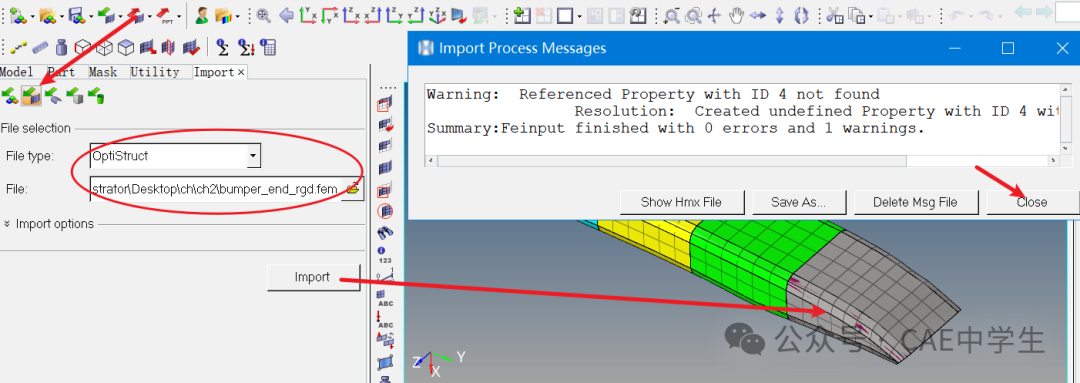
在Model组件中可以看到此文件包括5个组件,通过修改各组件颜色来区分,可以发现其中前3个都是空模型。
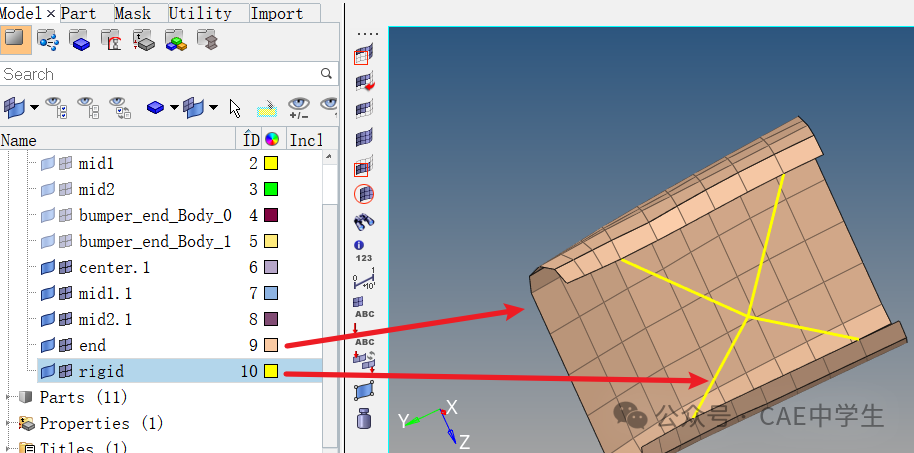
选中这3个组件,右击——Delete,即可删除。

2 保存与导出模型
这一节主要为了熟悉保存与导出操作。
以下分别以不同格式保存或导出模型。
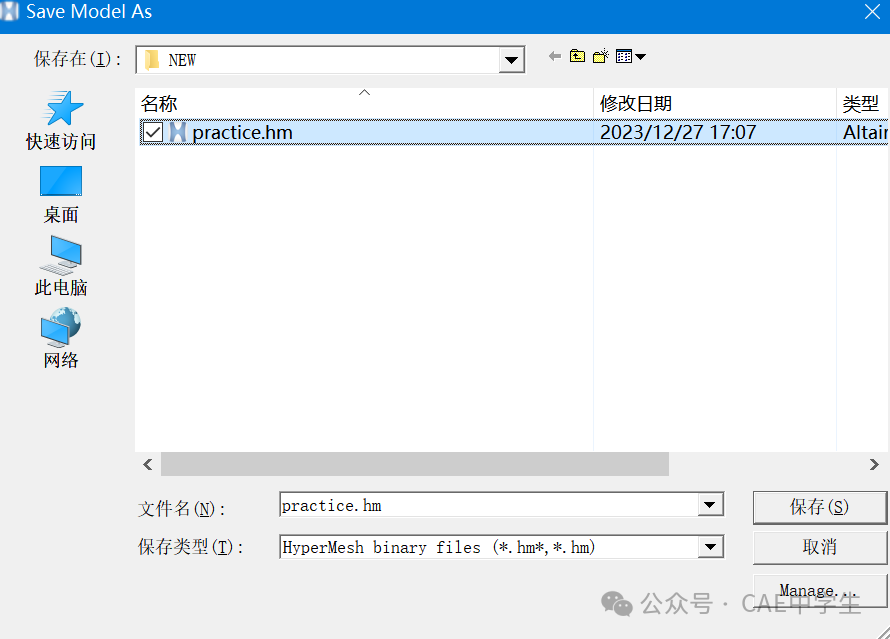
Step5 另存hm文件
通过File——Save As——Mode,保存为practice.hm文件,这是HM的专用格式,包括了所有处理信息。
Step6 导出几何模型
通过Export——Geomery,导出几何模型为practice.iges文件,只含几何模型,不含其他信息。

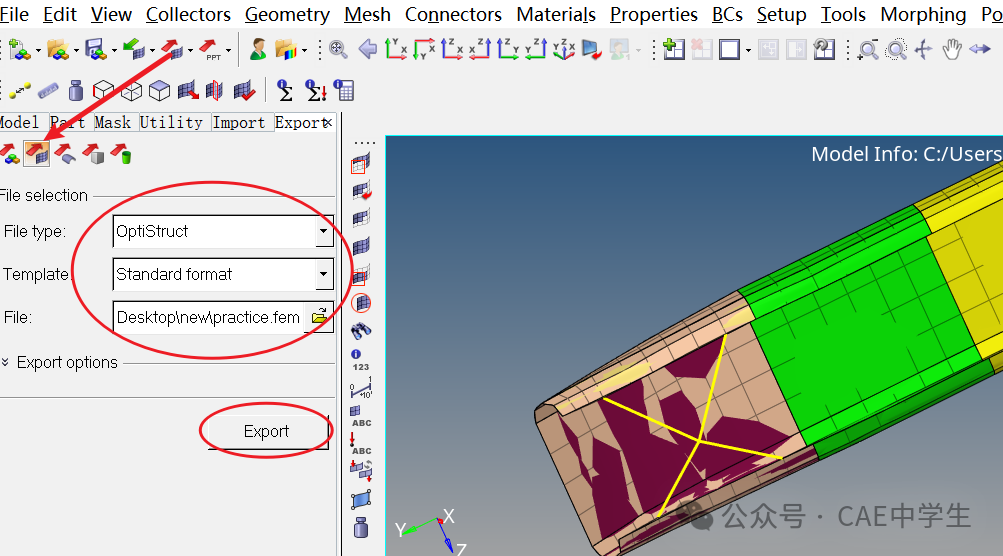
Step7 导出fem文件
通过Expot——Solver Deck导出OptiStruct的文件.fem,其中包含了除了几何模型以外的所有处理数据。
3 新建项目
这一节主要为了熟悉新建操作。
Step8 新建项目
通过New Model按钮或File——New新建项目,软件会提示是否删除当前数据,选择是。

Step9 导入文件
先后导入刚才保存的iges几何模型与fem文件,便得到了完整的几何模型+网格模型。

4 组件管理
这一节主要为了熟悉组件管理操作。
网格划分后,一般都需要将相同类型的网格移动到同一组件中,以便对它们赋予统一的属性。
Step10 新建组件
在浏览器空白处右击——Creat——Component,创建1个组件,取名为2Dmesh。

Step11 移动网格到新组件
切换到Mask浏览器,点击2D后面的“1”,便是仅仅显示2D单元,隐藏其他所有。
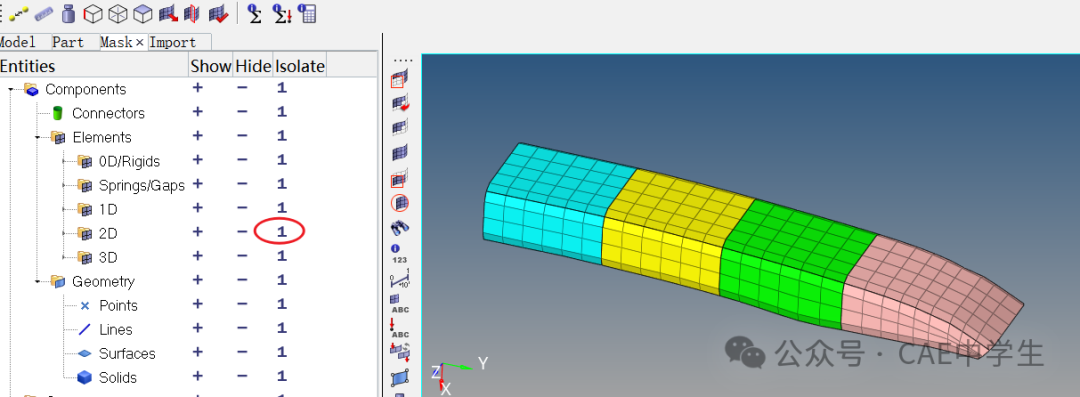
点击Collectors工具栏——Organize,这个工具专用于将模型移动到某个组件。
对象选中框中点击elems选择框,跳出选择菜单,选择displayed,即选中显示出来的所有单元,被选中的单元将以白色显示(也可按住Ctrl+左键拖动框选)。

点击dest Component按钮,跳出可供选择的所有组件,选择我们创建的2Dmesh组件,点击ruturn确定。

点击面板右侧的Move,即可将选中单元移动到指定组件中。
在Model浏览器中点击display all图标,将之前隐藏的几何和网格都显示。
将网格显示模式都修改为by comps,即随component的颜色。
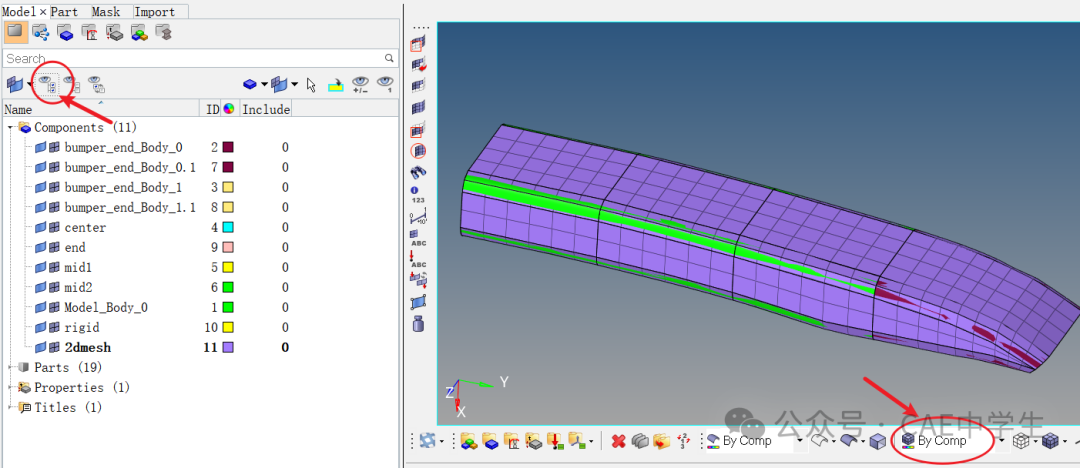
Step12 删除空组件
选择删除工具,对象选择comps,点击preview empty(预览空组件),状态栏提示找到6个空组件,点击delete entity删除它们,点击return退出。
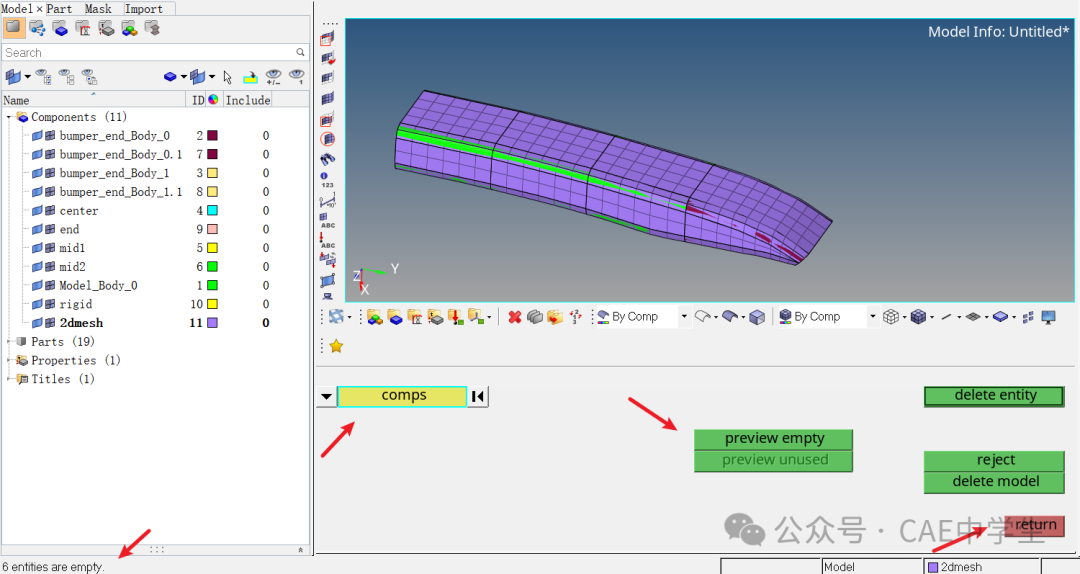
Step13 组件重新编号
选择菜单Collectors——Renumber——Components。

面板中选择single,对象选择comps——all,其他默认不修改,点击renumber,便对所有组件进行了重新编号。
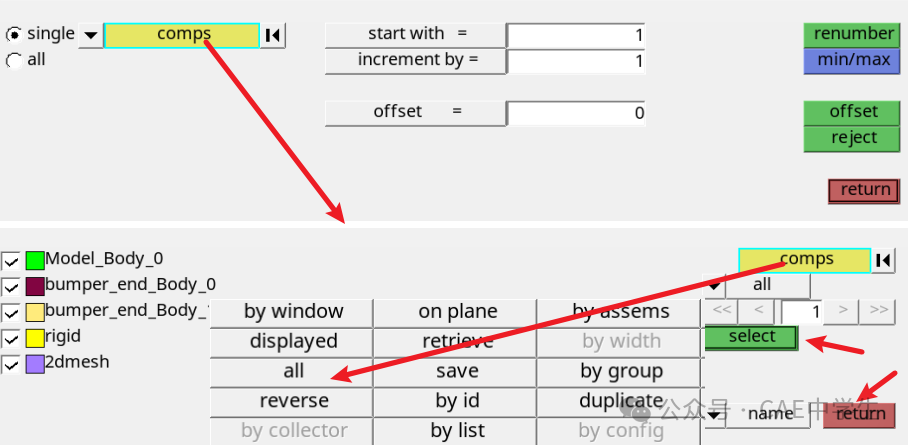
点击ID,可使组件按ID号排列整齐。

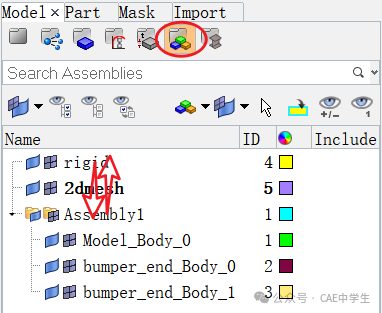
Step14 创建与管理Assembly
在浏览器空白处右击——Create——Assenbly,即可创建。将Model浏览器切换到Assembly显示模式如下。
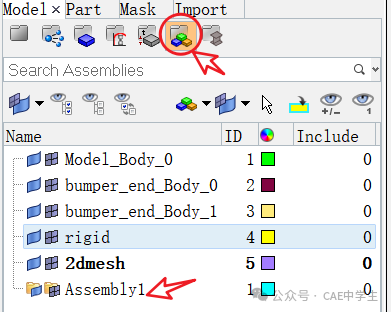
如果要将一个组件放入这个Assembly中,只需要直接拖动进去即可,要移出则从Asembly中拖出来。
5 显示操作
这一节主要为了熟悉显示操作。
Step15 显示操作
几何与网格可以按不同方式显示颜色,比如随Assenbly,随Component等,几何与网格还可以只显示线框,这些显示方式很简单,读者一用便会。
本文先介绍到这里,模型管理看似无关紧要,实际却是举足轻重,也是所有骚操作的基础,所谓不积跬步无以至千里,模型管理便是第一步。




