盲源分离技术专题第2篇 | 盲源分离的分类和假设条件

盲源分离主要分为超定、正定、欠定三种情况。混合信号由源信号混合而成，当混合信号数量大于源信号数量即为超定情况；当混合信号数量等于源信号数量即为正定情况；当混合信号数量小于源信号数量即为欠定情况。在实际的故障诊断过程中，不同传感器采集的振动信号为混合信号（已知），采集到的信号必定由不同的故障信号混合而成，这些故障信号为源信号（未知）。当然，从混合过程角度也可以将盲源分离分为线性瞬时混合模型、线性卷积混合模型、非线性混合模型。

瞬时混合模型要求传感器同时收集到各个源信号，其数学模型为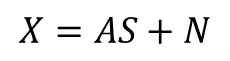：，X表示混合信号；S表示源信号；A表示混合矩阵，即瞬时混合过程；N表示噪声。具体模型如图1所示：

线性瞬时混合模型是盲源分离中一种相对理想的信号混合模式，其模型要求传感器同时采集到各个源信号，而在实际生活中，信号由于在传播过程中受到各种情况的干扰和影响，难免会出现时延，导致传感器所采集到的信号存在延迟的混合，即为线性卷积混合。

线性卷积混合模型比起瞬时混合模型更加符合实际信号的采集和传播过程，其数学模型为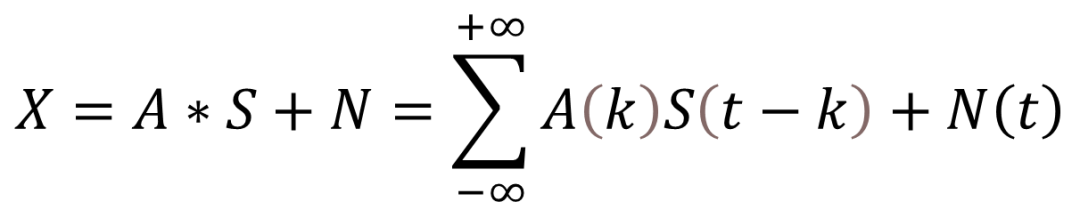：，*表示卷积运算，X表示混合信号；S表示源信号；A表示卷积混合系统；N表示噪声。具体模型如图2所示：

源信号的混合过程除了线性还存在非线性的混合过程，即传感器所采集到的混合信号是通过非线性的方式混合而成的。非线性混合模型的数学模型为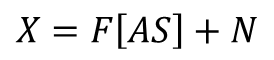：，X表示混合信号；S表示源信号；A表示未知的混合系统；F[ ]表示未知的非线性函数；N表示噪声。具体模型如图3所示：  

为了更好的理解盲源分离算法的整个脉络，绘制了如下分类图：  

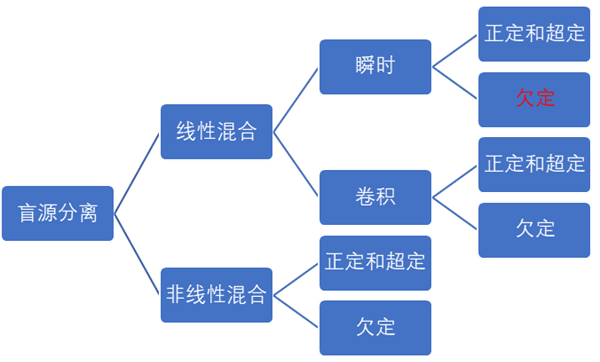
由于受到相关理论和技术的限制，相比于非线性混合模型来说，线性混合模型更简单，故线性模型被研究地更多、更深。在线性模型中，瞬时模型可以认为是卷积混合模型一种特殊情况，故长期以来，学者们研究工作主要集中在线性混合瞬时模型上。对于线性瞬时混合模型，出于经济和方便考虑，人们总是希望利用最少的传感器采集的信号去分析出更多的故障信号，故欠定线性瞬时混合模型更加符合实际情况，被更多的学者研究。经过笔者有限的调研，在盲源分离领域，最早研究的是线性瞬时混合模型的正定和超定，现阶段研究研最热的是瞬时欠定分离和卷积分离，非线性混合的研究较少、很难且缺少理论研究的支撑。随着数学理论研究的突破，相信在盲源分离领域的研究会越来越深。  

分析线性混合模型可知，已知条件为混合信号X（由传感器测得），一般整个分离过程是利用混合信号X先求得混合系统A，接着求得源信号S，最后利用各特征提取方法分析源信号。从数学的角度分析，求解过程会产生无数解，其中所要求的唯一解A、S也包含其中，其他解都是无意义的。为了能更快、更准确地求解，盲源分离必须满足一些假设条件才能找到正确解。假设条件如下：  

在源信号中，最多只存在一个高斯分布的信号，因为高斯分布的信号呈现出来是完全对称的，当高斯分布的信号经过线性混合后，其并不包含混合矩阵A中任意列向量的信息，仍然呈现为高斯分布。当源信号中有两个及以上信号呈现高斯分布时，盲源分离算法将无法求解A和S。  

源信号之间具有统计独立性或者统计不相关性，源信号的联合概率密度就等于各个源信号的边际概率密度的乘积，这种独立性条件是盲源分离的基础条件。  

混合矩阵A列满秩时，对于正定或超定能直接利用A的逆矩阵求解得到准确的S，对于欠定也能有解。  

满足了假设条件后，只能说盲源分离是能够分离得到源信号的，但是还是存在两个不确定性，即分离顺序的不确定性和分离幅值的不确定性。  

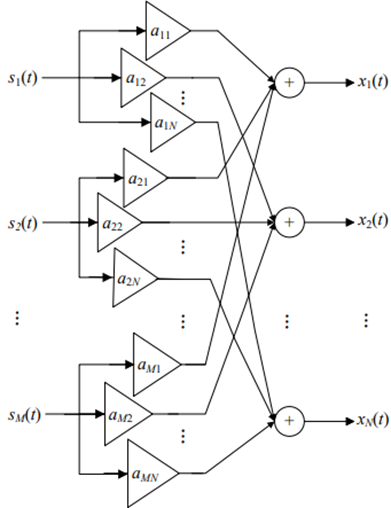
分离顺序的不确定性指的是源信号的位置和其对应的混合系统中列向量的位置同时变换时是不会影响结果的，这样就会造成源信号能全部分离，但是不能确定其顺序。分析图1可知，当把混合矩阵中的A的第一列和最后一列交换，相应的也交换源信号S中的S₁与S_N并不会影响混合的结果。  

分离幅值的不确定性是指源信号的幅值扩大或缩小多少倍，其对应的混合系统中的列向量缩小或扩大相应的倍数也是不会影响结果的，这样就会造成信号能全部分离，但其幅值无法确定。同样分析图1可知，当把混合矩阵中的A的第一列扩大或缩小N倍，相应的把S₁幅值缩小或扩大N倍并不影响混合结果。  

虽然盲源分离存在上述两种不确定性，但是并不会在实质上影响对源信号的识别，因为源信号全部被分离，且对应的特征的提取不会受到影响。例如，分析故障信号时都会分析频域、时频域特征，当信号幅值缩小或扩大时，并不会影响频域的特征提取分析，依然能够识别故障特征频率。

[1] 潘楠, 伍星, 迟毅林, 等. 基于频域盲解卷积的机械设备状态监测与故障诊断[J]. 振动与冲击, 2012, 31(12): 34-41. 

[2] 王晓燕.盲源分离方法及其在旋转机械故障诊断中的应用研究[D].燕山大学,2015. 

[3] 蔡龙.基于盲源分离的旋转机械故障诊断方法研究[D].燕山大学,2014.

[4] 李舜酩. 振动信号的盲源分离技术及应用[M]. 北京: 航空工业出版社, 2011: 24-29. 

[5] Jutten C, Herault J. Blind  separation of source Part I: An adaptive algorithm based on neuromimetic architecture[J]. Signal Processing, 1991, 24: 1-10. 

编辑：王畅

校核：李正平、张泽明、张勇、赵栓栓、陈凯歌、董浩杰

若需转载，请联系小编。