SMT(代理建模工具箱)之径向基函数
前言
代理建模工具箱 (SMT) 是一个开源 Python 包,由代理建模方法(例如径向基函数、克里金法)、采样方法和基准问题库组成。 SMT 旨在使开发人员能够轻松地在经过良好测试和详细记录的平台中实现新的代理模型,并使用户拥有一个可以使用和比较方法的代理建模方法库。
SMT 旨在成为代理建模(也称为元建模、插值和回归)的通用库,但其显着特点是专注于导数,例如用于基于梯度的优化。代理模型可以在数学上表示为:
y=f(x,xt,yt),
其中:

SMT 感兴趣的衍生品分为三类:
导数 (dy/dx):预测输出相对于模型评估输入的导数。
训练导数 ( dyt/dxt ):训练输出的导数,作为训练数据集的一部分给出,例如梯度增强克里金法。
输出导数 ( dy/dyt):预测输出相对于训练输出的导数,表示如果训练输出发生变化并且重新训练代理模型,预测将如何变化。
并非所有代理建模方法都支持或需要支持所有三种类型的导数;全部都是可选的。
安装:
pip install smt
方法:
| 预测一组点处的 dy_dx 导数。 |
| 预测一组点处的导数 dy_dyt。 |
| 预测一组点的输出值。 |
| 预测某点方差的导数 |
| 预测一组点的方差。 |
| 设置训练数据(导数)。 |
| 设置训练数据(值)。 |
| 训练模型 |
| 将训练数据(值)更新为先前设置的输入值。 |
| 将训练数据(值)更新为先前设置的输入值 |
Radial basis functions
径向基函数 (RBF) 代理模型将插值函数表示为基函数的线性组合,每个训练点都有一个基函数。 RBF 之所以如此命名,是因为基函数仅取决于基函数的预测点到训练点的距离。基函数的系数是在训练阶段计算的。 RBF 经常被扩充为全局多项式以捕捉总体趋势。
RBF 的预测方程为:
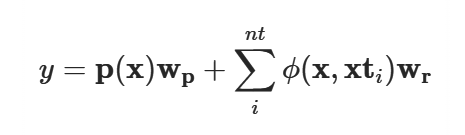

系数 Wp和 Wr通过求解以下线性系统来计算:
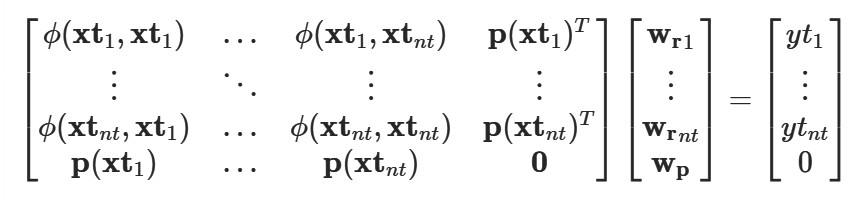
目前仅实现高斯基函数。这些由下式给出:
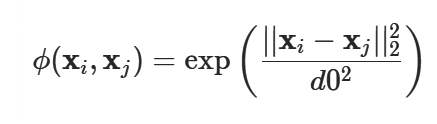
例子:
# 导入必要的库
import numpy as np
import matplotlib.pyplot as plt
from smt.surrogate_models import RBF # 导入径向基函数(RBF)插值模型
# 定义训练数据
xt = np.array([0.0, 1.0, 2.0, 3.0, 4.0]) # 输入数据点
yt = np.array([0.0, 1.0, 1.5, 0.9, 1.0]) # 对应的输出数据点
# 初始化并训练 RBF 插值模型
sm = RBF(d0=5) # 创建一个 RBF 插值模型,设置初始参数 d0=5
sm.set_training_values(xt, yt) # 设置模型的训练数据
sm.train() # 训练模型以拟合给定的数据
# 定义用于预测的 x 值范围和数量
num = 100
x = np.linspace(0.0, 4.0, num) # 在 [0.0, 4.0] 范围内生成 100 个均匀分布的点
# 使用训练好的 RBF 模型进行预测
y = sm.predict_values(x) # 对新的 x 值进行预测,得到预测的 y 值
# 绘制原始数据点和预测曲线
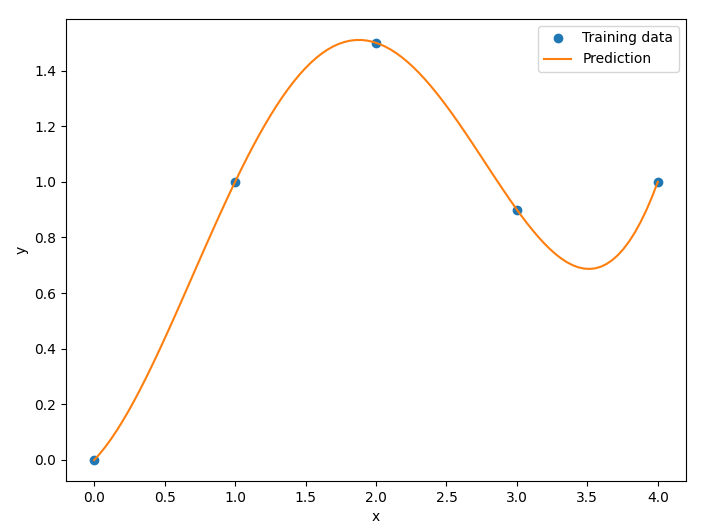
plt.plot(xt, yt, "o") # 绘制原始数据点
plt.plot(x, y) # 绘制 RBF 模型的预测结果
plt.xlabel("x") # 设置 x 轴标签
plt.ylabel("y") # 设置 y 轴标签
plt.legend(["Training data", "Prediction"]) # 添加图例,显示“训练数据”和“预测”标签
plt.show() # 显示绘制的图形