图3 Re=100时方腔速度矢量图(左:VirtualFlow,右:OpenFOAM) 图4 Re=100方腔层流计算结果与文献[1,2]对比 图3给出了VirtualFlow及OpenFOAM计算所得Re=100时方腔速度云图及矢量图,由图可知两款软件计算结果大体相同,均在贴近方腔上板形成一个较大旋涡结构。如图 4将Re =100时的计算结果(沿X =H/2中心线u的变化和沿Y =H/2中心线v的变化)与文献[1]中的数值计算结果及文献[2]中的基准解进行对比分析,可以看到VirtualFlow计算结果与OpenFOAM计算结果基本一致,而两款软件与文献之间的偏差也较小。  图5 Re=400时方腔速度矢量图(左:VirtualFlow,右:OpenFOAM)
图5 Re=400时方腔速度矢量图(左:VirtualFlow,右:OpenFOAM) 图6 Re=400方腔层流计算结果与文献[1,3]对比
图5给出了VirtualFlow及OpenFOAM计算所得Re=400时方腔速度云图及矢量图,由图可知随着Re的增大,旋涡结构逐渐下移,且右下角旋涡尺度增大,两款软件计算所得速度分布结构相似。图6将 Re =400时的计算结果(沿X =H/2中心线u的变化和沿Y =H/2中心线v的变化)与文献[1]中的数值计算结果及文献[3]中的基准解进行了对比,可以看到VirtualFlow、OpenFOAM计算结果与文献中的数值结果及基准解接近。  图7 Re=1000时方腔速度矢量图(左:VirtualFlow,右:OpenFOAM)
图7 Re=1000时方腔速度矢量图(左:VirtualFlow,右:OpenFOAM)
图8 Re=1000方腔层流计算结果与文献[4]对比
图7给出了CTPA计算所得Re=1000时方腔速度云图及矢量图,由图可知Re=1000方腔内旋涡结构相较于Re=400时方腔内的漩涡结构更大且更加饱满,下方角落均卷起较大的漩涡。对比两款软件计算结果,可见两款软件速度矢量分布相似,仅在局部数值上有稍微偏差。图8将Re =1000时的计算结果(沿X =H/2中心线u的变化和沿Y =H/2中心线v的变化)进行对比分析,由图可知两款软件速度分布大致相同,仅在局部有偏差,其中VirtualFlow计算结果与文献[4]中的基准解更加吻合。将流场中心(0.5,0.5)处的速度计算结果与文献[4]中的基准解进行了对比,其中VirtualFlow计算所得u=-0.0612757、v=0.025469,OpenFOAM计算所得u=-0.0535887 、v=0.0297844,而文献[4]中基准解为u=-0.0608、v=0.02526,VirtualFlow计算结果更接近基准解。
通过对VirtualFlow及OpenFOAM顶盖驱动方腔流计算结果对比分析可知两款软件均可用于一般性流动问题,求解精度与相关文献偏差不大。VirtualFlow相较于OpenFOAM具有便捷高效的网格生成方法、清晰简洁的边界加载方式、完善合理的界面布局,能够更好的上手体验。用户通过采用VirtualFlow模拟经典案例cavity,可以更好的理解计算流体力学分析流程,了解计算流体力学相关概念。OpenFOAM是CFD数值计算的C++自由软件工具包,其描述张量和偏微分方程的语法与被求解的方程本身相似,有助于用户在其基础上添加相关方程模型。在VirtualFlow中,通过高级初始化功能及高级UDF功能同样可以实现相关模型的添加及修正,高级初始化功能及高级UDF功能采用面向对象编程语言C++进行开发,对于熟悉OpenFOAM二次开发或Fluent UDF开发的工程师来说能够更容易掌握。一般情况下,通过VirtualFlow界面选择UDF模版,在模版基础上进行开发以实现相关功能,如果需要对求解器进行深层次的二次开发,可与我司工程师联系进行定制开发。 图 9 VirtualFlow中UDF模版选择
[1]屠珊,孙弼,毛靖儒.用Richardson外推法分析流动传热层流问题的不确定度[J].西安交通大学学报,1999,33(11);47~50.[2]RhodesT, Acharya S. An adaptive differencing scheme for flow and heat transferproblems. Numerical Heat Transfer, Part B,1993,23(2):153~173.[3]CorniniG,Manzan M ,Nonino C .Finite element solution of the streamfunction —vorticity equations for incompressible two-dimensional flows . InternationalJournal for Numerical Methods in Fluids.1994,19(6 ):513-525[4] Rek Z , Skerget L. Boundary element method for steady 2Dhigh-Reynolds-number flow. International journal for Numerical Methods inFluids.1994,19(4):343-361 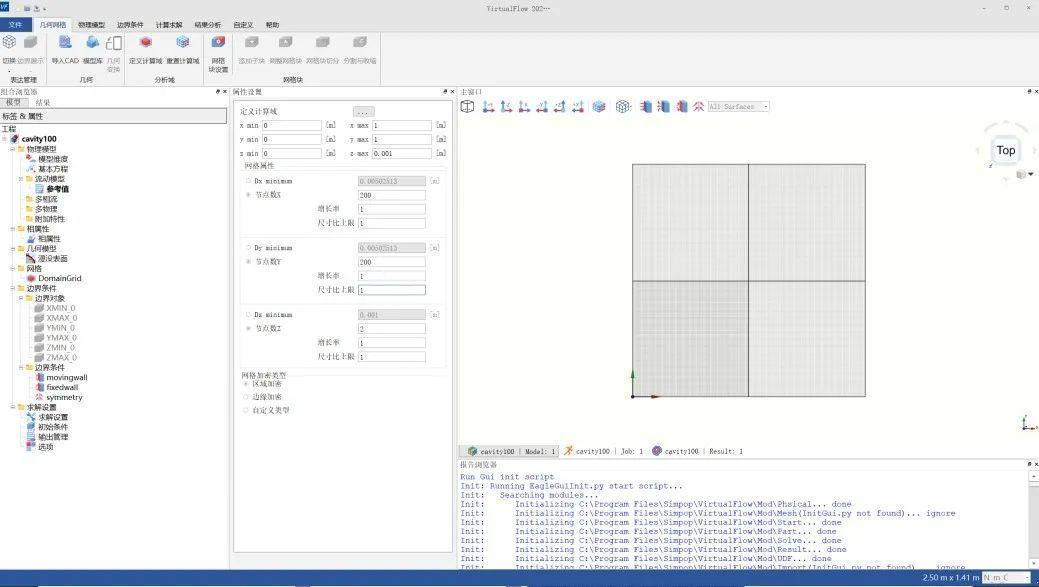
 图2 方腔物理模型及网格划分
图2 方腔物理模型及网格划分 
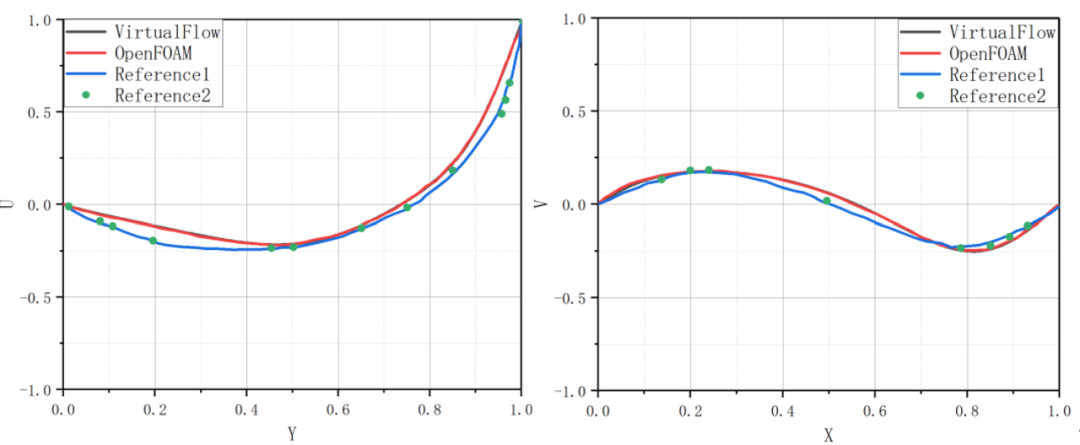
 图5 Re=400时方腔速度矢量图(左:VirtualFlow,右:OpenFOAM)
图5 Re=400时方腔速度矢量图(左:VirtualFlow,右:OpenFOAM) 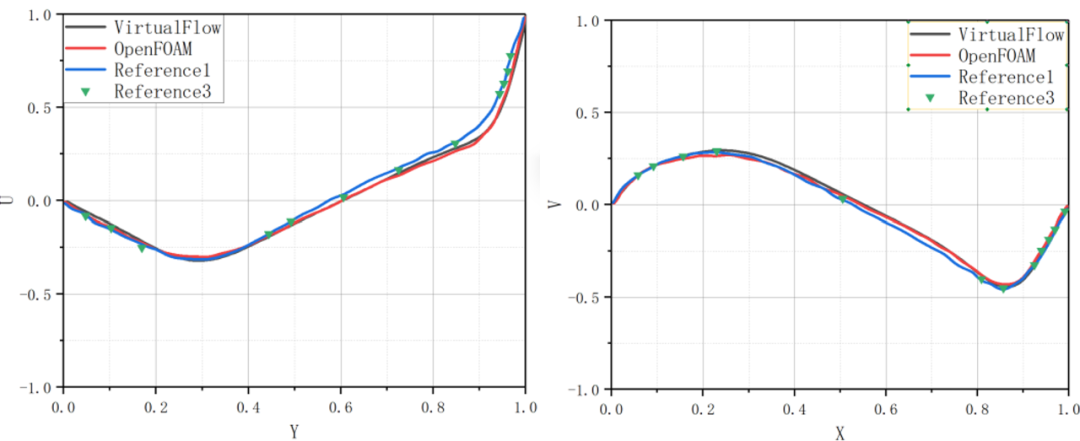
 图7 Re=1000时方腔速度矢量图(左:VirtualFlow,右:OpenFOAM)
图7 Re=1000时方腔速度矢量图(左:VirtualFlow,右:OpenFOAM)





