屈曲失稳分析不能使用对称模型?实例表明不完全是这样!
学员群中有人提出看法:屈曲失稳分析不能使用对称模型。同理,振动模态分析也不能使用对称模型。

在某些行业,对称分析确实很常见,比如压力容器行业。使用对称分析最大的优势是:在不降低分析精度的前提下能大幅减少计算规模。
屈曲失稳分析和振动模态分析是不是一定不能用对称分析?其实这也要看情况。如果某阶屈曲变形或模态变形是对称的,那么使用对称分析是可行的;相反,则是不可行的。
本文通用一个简单的压杆稳定问题,来验证这个结论:
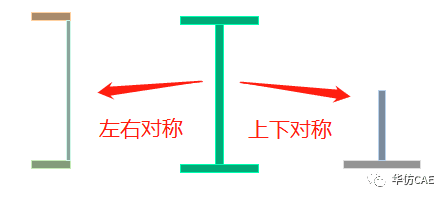
1)对称变形,可以用对称分析;
2)不对称变形,不能用对称分析;
一根杆件受压,如下图所示。

杆件失稳的临界载荷计算公式。


H型立柱如下图所示。

横截面惯性矩如下图所示。
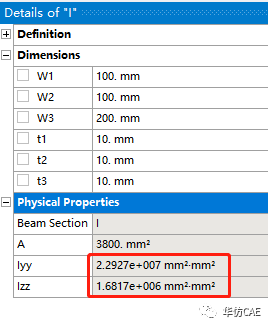
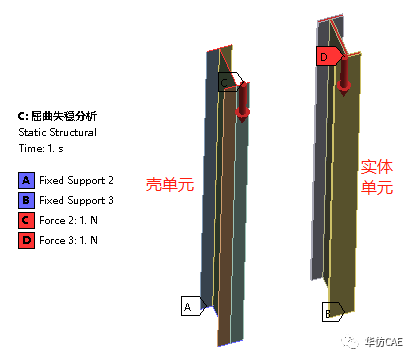
一端固定,另一端自由。自由端施加单位压力。
公式计算得到的临界载荷:
弱轴:3.688E5 N
强轴:5.028E6 N
仿真得到的临界载荷:
弱轴:


强轴:

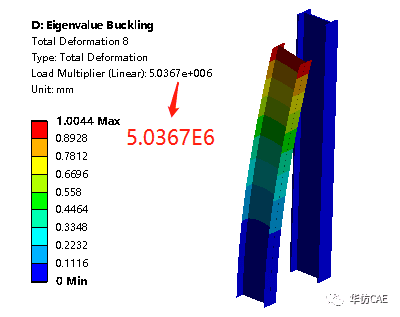
公式解和仿真解高度一致,相互验证。
使用两种对称分析(实体单元):
一端固定,另一端自由。因为是对称分析,自由端施加单位压力的一半,使用无摩擦约束作为对称定义。
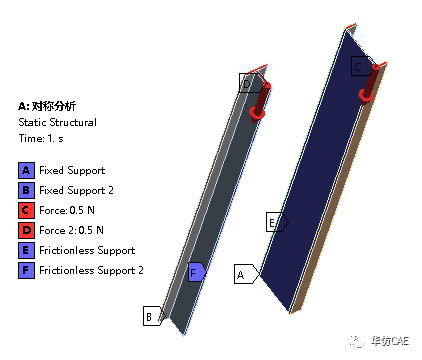
仿真得到的临界载荷:
弱轴:
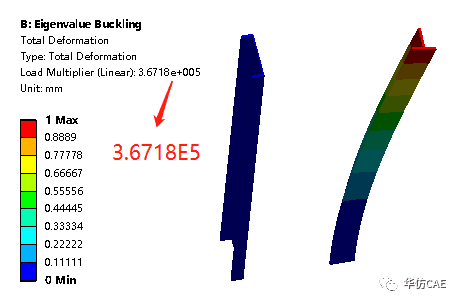
强轴:

上下对称分析得到了正确的绕弱轴的临界载荷,左右对称分析得到了正确的绕强轴的临界载荷。所以屈曲失稳分析不能使用对称分析的结论并不完全正确。
可以发现,如果以屈曲变形的对称面作为对称分析的对称面,则分析结果不受影响。振动模态分析中也是这个道理。
对于实际工程,很多时候只需要获得第一阶临界载荷,并且大部分情况下,第一阶屈曲变形的趋势是知道的。所以对于实际工程,如果有降低计算规模的硬指标,屈曲分析也可以酌情使用对称分析。当然使用完整模型也没问题。
如果使用完整模型分析,笔者还有一个建议,屈曲分析对网格大小不敏感,所以为了降低计算规模,网格尺寸可以更粗疏一点。
来源:华仿CAE