机械设计手册中没有的销轴连接形式,如何计算应力?仿真告诉你答案!
笔者前作《《机械设计手册》给我力量!销轴连接定义为球铰是完全合理的》探讨了销轴连接对应的joint类型。但是笔者最近遇到了这种销轴。

在《机械设计手册》中找不到对应类型。


领会已有销轴计算公式的保守精神,本文的销轴连接的计算公式也应该基于两个假设:
1)销轴和轴套之间的反力沿轴向是均布的;
2)忽略轴套对销轴抗弯的加强作用;
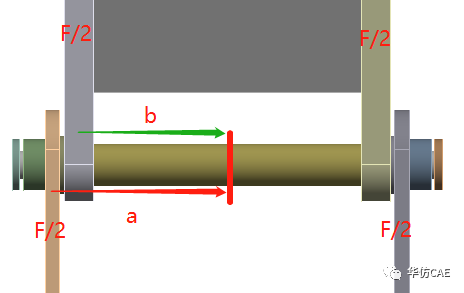
销轴跨中的弯矩:
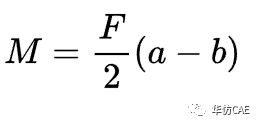
销轴跨中的弯曲应力:

设F=10000N,a-b=36mm,d=39mm

根据计算公式,销轴跨中的弯曲应力:
σ=30.34MPa
使用joint球铰定义销轴和轴套的连接关系。仿真得出的弯曲应力和公式计算基本一致,再次证明球铰类型的正确性。

真实的销轴连接应该是摩擦接触。

定义摩擦接触。注意因为是间隙配合,需要定义Damping Factor。

仿真得出的弯曲应力如下图所示。


可以发现摩擦接触下的弯曲应力和计算公式差别很大,和joint球铰的差别也大。这是为什么呢?
这里需要再次强调计算公式的两个假设:
1)销轴和轴套之间的反力沿轴向是均布的;
2)忽略轴套对销轴抗弯的加强作用;
对于销轴跨中,没有轴套束缚,所以假设二成立。
对于摩擦接触,假设一并不能成立,从销轴和轴套的配合面的接触压力可以看出,反力沿轴向并不均布。并且可以看出,这种反力分布规律导致对跨中的力矩会严重偏小。所以摩擦接触下的弯曲应力比计算公式小很多。


计算公式是保守的,使用joint球铰分析结果接近计算公式,也是保守的。
定义摩擦接触更符合现实情况,但摩擦接触求解耗时,如果模型中有大量销轴,使用大量摩擦接触,求解会极其耗时,甚至难以收敛。(理论上,只要时间步足够小,也是可以收敛的,但如果时间步极小,可能求解总耗时难以接受)
来源:华仿CAE




