基于C#的薄板有限元程序计算(理论+代码)
原创: 高工
知乎主页:https://www.zhihu.com/people/duo-du-33
这次主要想解决的还是局部荷载的问题,虽然荷载规范给出了相应解法,但是感觉上还是心里没底,说到底近似算法还是没有数值解靠谱,而且局部荷载对双向板的影响也很难用单向板的受力模式解释,所以最后还是觉得怎么也得上有限元方法,于是用C#做了一个有限元计算程序。
选择C#主要是考虑到这玩意干什么都行,毕竟做结构的话常用软件AutoCAD、Revit、SAP2000、Rihno、Grasshopper都支持C#做二次开发,而且也有http://ASP.NET可以做后端开发,前端框架选择目前比较时髦的Vue3+Element-ui。
计算程序截图如下:
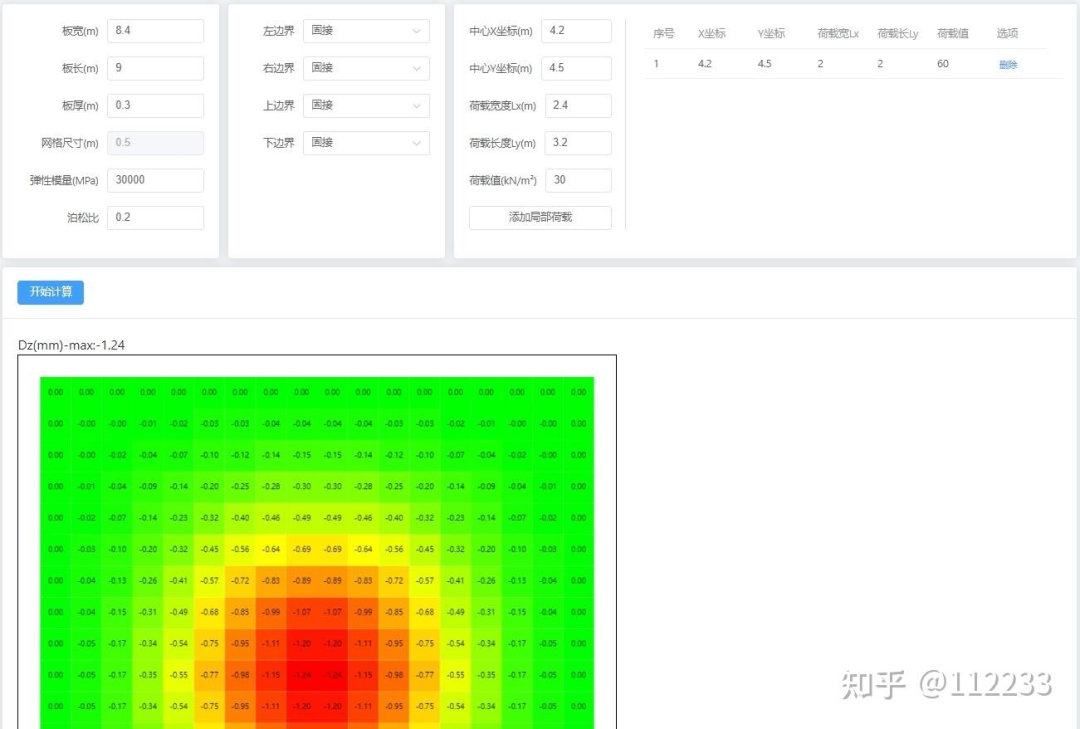
薄板基本理论
基本方程
稍有常识的工程师都知道,有限元计算时一个节点有6个自由度,对于矩形板单元来讲,4个节点24个自由度算起来太麻烦,所以1850年Kirchhoff给出了经典的薄板壳理论,Kirchhoff理论的基本假设有三个:

(1)忽略层与层之间的挤压应力,也就是说Z向应变
因此挠度 与坐标 无关,仅为 、 坐标的函数 。
(2)变形前垂直于中面的线元,变形后仍垂直于变形后的中面,忽略剪切应力 和 引起的变形。因此,
对上述两式进行积分可得,式中C1、C2为常数:
(3)中面上的点无平行于中面的位移,即当z=0时: 代入上文中的两式可得:
根据以上Kirchhoff理论,可得几何方程如下,式中为 泊松比, 为弹性模量:
可得物理方程如下:
即三个未知量、三个方程。写成矩阵形式:
式中,应力应变关系矩阵 和应变矩阵 记为:
式中:
可得弹性关系矩阵D:
内力矩是对中性面力矩的合成,即力矩矩阵 如下:
位移场
考虑矩形单元有4个节点,每个节点有三个参数:挠度w、绕x轴转动θx、绕y轴转动θy,可将单元的节点位移向量记为:
单元中任意一点的的位移可通过拉格朗日插值得到:
用矩阵表示为:
由于 有12个参数,因此在确定形函数时,我们采用Lagrange函数进行差值,可得二维k次完全多项式的三角形排列如下:
12个自由度,假定形函数如下:
最后两项是为了避免升次导致计算复杂,因此选择了对称的两个3次项。
写成矩阵形式:
为确定待定系数 可将节点1,2,3,4的坐标代入w及其导数的表达式,可得下列方程组:
将上式写成矩阵形式:
即:
通过求逆可以确定待定参数 :
可得:
即矩形薄板单元的形函数矩阵,可按节点分块写为:
式中:(i=1,2,3,4)
代入广义应变向量:
式中B为应变矩阵:
刚度矩阵
单元应变能:
根据最小势能原理,单元刚度矩阵如下:
式中a、b是单元边长,Ω=ab是单元面积.
面力
节点力向量F记为:
集中力只要加在相应的自由度上就可以,均布力需要按下式施加:
程序设计
ThinSlabObj对象
只考虑矩形板,创建一个薄板对象,这个对象指的是一块未分割单元的整体矩形板,它具有以下属性:

代码如下:
public class ThinSlabObj
{
public double Lx { get; set; }
public double Ly { get; set; }
public double Thick { get; set; }
public double MaxElemLeng { get; set; }
public double E { get; set; }
public double Nju { get; set; }
public Nodes Nodes { get => _nodes; set => _nodes = value; }
public ThinSlabElems ChildElems
{ get => _thinSlabElems; set => _thinSlabElems = value; }
public int DofCount => _nodes.Count * 3;
}
Node对象Node是有限元节点对象,它继承自PointXY,继承了父类的X坐标、Y坐标等信息,并且存储了节点Id、自定义名称Name以及自由度Id等数据,其属性如下:
 代码如下:
代码如下:
public class Node : PointXY
{
public int Id { get; set; }
public string Name { get; set; }
public int DxId { get; set; }
public int DyId { get; set; }
public int DzId { get; set; }
public int RxId { get; set; }
public int RyId { get; set; }
public int RzId { get; set; }
public double Dx { get; set; }
public double Dy { get; set; }
public double Dz { get; set; }
public double Rx { get; set; }
public double Ry { get; set; }
public double Rz { get; set; }
public double Fx { get; set; }
public double Fy { get; set; }
public double Fz { get; set; }
public double Mx { get; set; }
public double My { get; set; }
public double Mz { get; set; }
}
ThinSlabElem对象
这是矩形板分割后的子单元对象,

代码如下:
public class ThinSlabElem
{
public int Id { get; set; }
public Nodes Nodes { get => _nodes; set => _nodes = value; }
public double E { get; set; }
public double nju { get; set; }
public double Thick { get; set; }
public double Lx => GetLx();
public double Ly => GetLy();
}
BoundryCondition对象这是板边界条件对象,保存板四条边的边界条件,属性如下:

代码如下:
public struct BoundaryCondition
{
public eBoundaryCondition Left { get; set; }
public eBoundaryCondition Right { get; set; }
public eBoundaryCondition Top { get; set; }
public eBoundaryCondition Bottom { get; set; }
}
枚举类型eBoundaryCondition代码如下:
public enum eBoundaryCondition
{
Solid = 1,
Hinge = 2,
Free = 3,
}
DistriLoad对象这是均布荷载的对象,用来保存局部荷载的相关信息,其属性如下:

代码如下:
public class DistriLoad
{
public PointXY Location { get; set; }
public double Lx { get; set; }
public double Ly { get; set; }
public double LoadValue { get; set; }
}
ThinSlabFeaSolver对象
这是有限元求解器对象,输入ThinSlabObj、BoundryCondition、DistriLoad对象进行求解,得到每个节点的变形和内力。这些结果储存在输入的ThinSlabObj对象中,调用该对象的Nodes属性可以获得相关数据。属性如下:


代码如下:
public class ThinSlabFeaSolver
{
private ThinSlabObj _slabObj = new ThinSlabObj();
private BoundryCondition _bondCon = new BoundryCondition();
private List<DistriLoad> _disLoads = new List<DistriLoad>();
}
程序运行过程
创建薄板对象
创建宽8m,长9m,厚300mm,分割单元最大长度500mm,弹性模量30000MPa,泊松比0.2的薄板对象:
internal class Program
{
static void Main(string[] args)
{
var width = 8;
var length = 9;
var thick = 0.300;
var maxElemLeng = 0.500;
var e = 30000000;
var nju = 0.2;
var slabObj = new ThinSlabObj(width, length, thick, maxElemLeng, e, nju);
}
}
创建边界条件对象
创建四边固接的边界条件对象:
internal class Program
{
static void Main(string[] args)
{
//接上文
var bc = new BoundaryCondition()
{
Left = eBoundaryCondition.Solid,
Right = eBoundaryCondition.Solid,
Top = eBoundaryCondition.Solid,
Bottom = eBoundaryCondition.Solid
};
}
}
创建局部荷载对象创建中心点位于(4,2),宽2m,长2m,荷载值为30kN/m²的局部荷载:
internal class Program
{
static void Main(string[] args)
{
//接上文
var disLoadX = 4;
var disLoadY = 2;
var disLoadLx = 2;
var disLoadLy = 2;
var disLoadVal = 30;
var disLoad =
new DistriLoad(
new PointXY(disLoadX, disLoadY), disLoadLx, disLoadLy, disLoadVal);
}
}
创建求解器对象并求解
internal class Program
{
static void Main(string[] args)
{
//接上文
var slabFeaSolver = new ThinSlabFeaSolver(slabObj, bc, disLoad);
slabFeaSolver.Solve();
}
}
Solve()方法将板分割为子单元,并对节点、子单元、节点自由度进行编号
public void Solve()
{
//分割板构件,给单元和节点编号
_slabObj.DivideIntoElem();
//给节点的每个自由度编号
int dofCount = _slabObj.GetDofId();
}
组装整体刚度矩阵
public void Solve()
{
//接上文
//组装整体刚度矩阵
var mxK = _slabObj.AssembleGlobalK();
}
生成节点力矩阵
public void Solve()
{
//接上文
//节点力赋值
var vtF = new Vector(dofCount);
foreach (var node in _slabObj.Nodes)
{
foreach (var disLoad in _disLoads)
{
var xList = new List<double>();
var yList = new List<double>();
node.IntereactElems.ForEach(o =>
o.Nodes.ForEach(
fnode => xList.Add(fnode.X)));
node.IntereactElems.ForEach(o =>
o.Nodes.ForEach(
fnode => yList.Add(fnode.Y)));
var maxX = xList.Max();
var minX = xList.Min();
var maxY = yList.Max();
var minY = yList.Min();
var X0 = node.X - (node.X - minX) * 0.5;
var X1 = node.X + (maxX - node.X) * 0.5;
var Y0 = node.Y - (node.Y - minY) * 0.5;
var Y1 = node.Y + (maxY - node.Y) * 0.5;
var area = GetIntereactArea(
X0, X1, Y0, Y1,
disLoad.Location.X - 0.5 * disLoad.Lx,
disLoad.Location.X + 0.5 * disLoad.Lx,
disLoad.Location.Y - 0.5 * disLoad.Ly,
disLoad.Location.Y + 0.5 * disLoad.Ly
);
var dofId = node.DzId;
vtF[dofId] += -1 * disLoad.LoadValue * area;
}
}
}
根据边界条件提取需要去除的自由度ID并对整体刚度矩阵和节点力矩阵进行划行划列:
public void Solve()
{
//接上文
//边界条件
//消除自由度
var lstCullDof = new List<int>();
foreach (var node in _slabObj.Nodes)
{
//左下
if (Math.Abs(node.X - 0) < tolerance &&
Math.Abs(node.Y - 0) < tolerance)
{
lstCullDof.AddRange(
GetRestrainedDof(node, _bondCon.Bottom, _bondCon.Left));
}
//左上
else if (Math.Abs(node.X - 0) < tolerance &&
Math.Abs(node.Y - SlabObj.Ly) < tolerance)
{
lstCullDof.AddRange(
GetRestrainedDof(node, _bondCon.Top, _bondCon.Left));
}
//右下
else if (Math.Abs(node.X - _slabObj.Lx) < tolerance &&
Math.Abs(node.Y - 0) < tolerance)
{
lstCullDof.AddRange(
GetRestrainedDof(node, _bondCon.Bottom, _bondCon.Right));
}
//右上
else if (Math.Abs(node.X - _slabObj.Lx) < tolerance &&
Math.Abs(node.Y - SlabObj.Ly) < tolerance)
{
lstCullDof.AddRange(
GetRestrainedDof(node, _bondCon.Top, _bondCon.Right));
}
//左
else if (Math.Abs(node.X - 0) < tolerance)
{
lstCullDof.AddRange(
GetRestrainedDof(node, _bondCon.Left));
}
//右
else if (Math.Abs(node.X - _slabObj.Lx) < tolerance)
{
lstCullDof.AddRange(
GetRestrainedDof(node, _bondCon.Right));
}
//上
else if (Math.Abs(node.Y - SlabObj.Ly) < tolerance)
{
lstCullDof.AddRange(
GetRestrainedDof(node, _bondCon.Top));
}
//下
else if (Math.Abs(node.Y - 0) < tolerance)
{
lstCullDof.AddRange(
GetRestrainedDof(node, _bondCon.Bottom));
}
}
//划行划列
var mxKCull = mxK.CopyCull(lstCullDof.ToArray());
var vtFCull = vtF.CopyCull(lstCullDof.ToArray());
}
行列式求解并提取各自由度变形
线性方程组求解用的是LU分解法
public void Solve()
{
//接上文
var result0 = NewMatrixSolver.MatrixSolverTypeLU(mxKCull.Data, vtFCull.Data);
var resultDisp = new Vector(result0);
}
将节点位移回代子单元刚度矩阵即得节点内力
public void Solve()
{
//收集节点内力
_slabObj.ChildElems.ForEach(o => o.CollectNodeForce());
}
CollectNodeForce()方法如下:
public void CollectNodeForce()
{
var mxKe = this.GetKe();
var lstDisp = new List<double>();
foreach (var node in _nodes)
{
lstDisp.Add(node.Dz);
lstDisp.Add(node.Rx);
lstDisp.Add(node.Ry);
}
var vtDisp = new Vector(lstDisp.ToArray());
var vtForce = mxKe * vtDisp;
}
小结写到这发现我写的逻辑太复杂,根本没法掰开了讲,所以只能把整体思路过一遍,这里很多具体的函数就不展开了,有兴趣的同学可以跟着我的思路自己写一写, 一共不到1000行代码就能弄完。
前端设计
工程师就追求个实用,一共没几个参数,一眼就能看懂,就不细讲了,这里由于服务器性能的原因,网格尺寸做了限制,板尺寸也限制在20m以下。

点击开始计算之后结果如下:
节点位移:

绕x轴弯矩

绕y轴弯矩

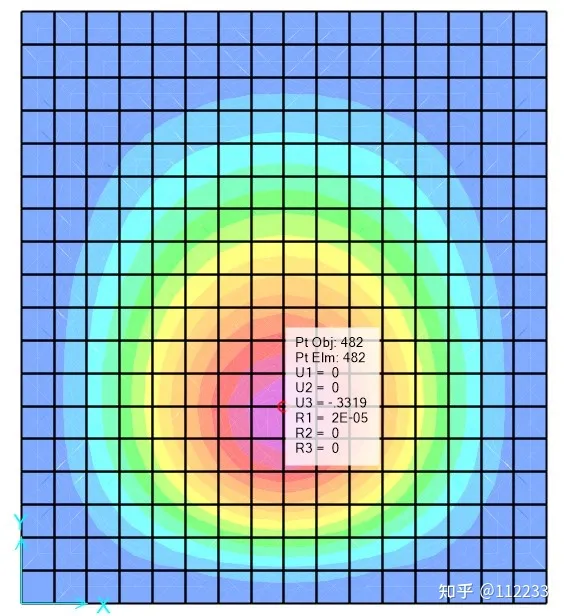
与SAP2000对比
Dz
 Mx
Mx
 My
My


基本一致吧,我看了看位移基本上吻合的最好,差距都在1%以内,但是弯矩就差的多一点,这个确实很奇怪。可能还是刚度矩阵积分的方法不太一样?


