《机械设计手册》给我力量!销轴连接定义为球铰是完全合理的
关于销轴连接,先引用闻老师主编的《机械设计手册》的内容。


再引用成老师主编的《机械设计手册》的内容。

一起来理解下,计算公式的由来。
1)计算挤压应力:轴力除以承压面的投影面积;
2)计算剪切应力:轴力除以抗剪面积;
3)计算弯曲应力:如下。
销轴跨中的弯矩M:

销轴跨中的抗弯模量W:
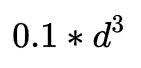
销轴跨中的弯曲应力:
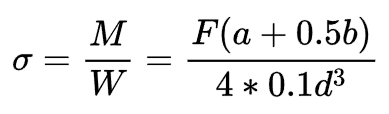
销轴的挤压应力和剪切应力的计算公式一目了然,无需验证。现通过仿真分析验证销轴的弯曲应力的计算公式:
假设a=20mm,b=30mm,d=10mm,F=20N;

销轴跨中的弯矩M=10*(10+7.5)=175N.mm。

销轴跨中的弯曲应力σ=1.75MPa

从力学原理出发,可以推断出《机械设计手册》中销轴弯曲应力的计算公式,必须建立在如下假设之上:
1)销轴和轴套之间的反力沿轴向是均布的;
2)忽略轴套对销轴抗弯的加强作用;
设a=20mm,b=30mm,d=10mm。为突出弯曲应力,设F=2000N,按照《机械设计手册》的计算公式,弯曲应力则约为175MPa。
当joint的类型为Revolute,弯曲应力远小于175MPa。

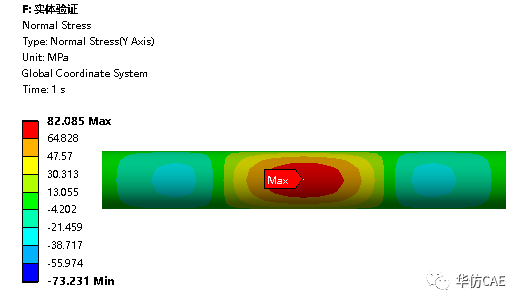
当joint的类型为Cylindrical,弯曲应力明显小于175MPa。
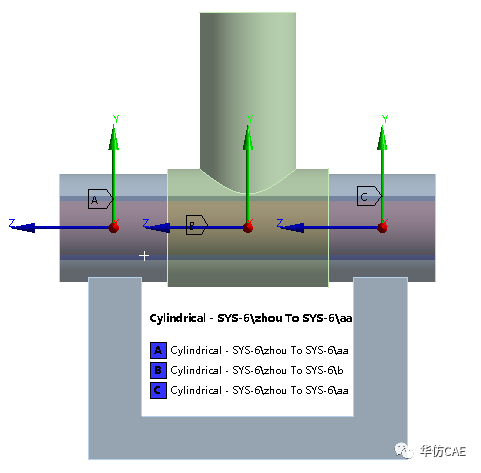

当joint的类型为Sphere,弯曲应力略大于175MPa。


为什么轴套和销轴设置为球铰关系,计算出来的弯曲应力结果和《机械设计手册》的计算公式更接近呢?
这是因为:《机械设计手册》中弯曲应力的计算公式忽略了轴套对销轴抗弯的加强作用!
实际轴套对销轴的抗弯肯定有加强作用,并且配合间隙越小,配合长度越大,加强作用就会越显著。《机械设计手册》中弯曲应力的计算公式显得更加保守。
在joint类型中,Revolute和Cylindrical都存在轴套对销轴的抗弯加强作用,所以销轴的弯曲应力偏小。Sphere类型能完全忽略轴套对销轴的抗弯加强作用,所以结果最保守!
来源:华仿CAE




