轿厢垂直方向晃动的机理、研究模型、解决方案、快速分析等
电梯公司对电梯运行过程中的轿厢振动是有严格要求的,一般使用EVA或DT-4设备监测振动波形的峰峰值和A95值。
轿厢振动可以分为两类:轿厢整体晃动;轿厢零部件振动。
本文使用电梯模型和弹簧振子模型,研究轿厢整体晃动的解决方案。
需要说明的是,电梯系统本身是非线性动力学系统,使用线性分析只是一种简化方法。通过线性分析,可以解决振动中的某些频率问题,从而将振动控制在允许范围内。
电梯模型(简化后)如下图所示。

由于研究目的是解决轿厢整体晃动问题,所以可以将几何模型刚体化,也就不存在网格划分需求。
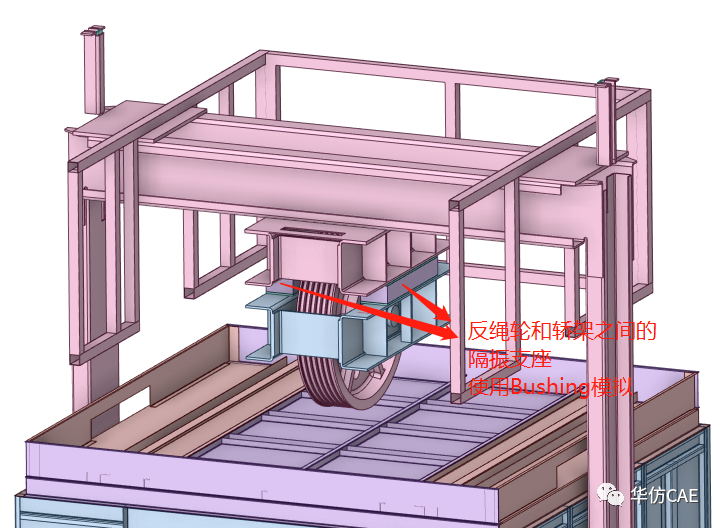

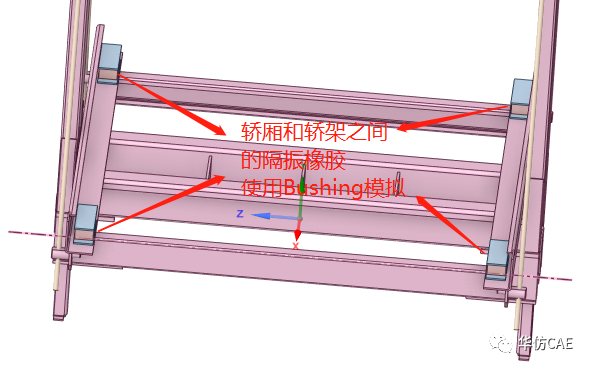



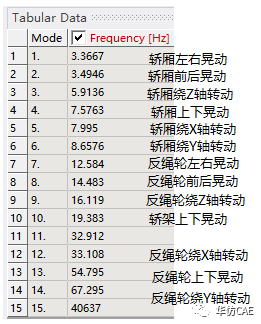
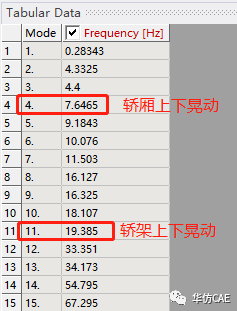
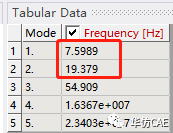
轿架只释放Z向自由度。仿真获得1个轿架晃动模态,6个轿厢晃动模态,6个反绳轮晃动模态。
这里只释放轿架Z向自由度存在争议。实际如果使用滚动导靴,轿架的X和Y方向自由度可以通过弹簧的形式定义约束;如果使用滑动导靴,X和Y方向自由度可以假设为释放。
下图为释放轿架X和Y方向自由度的模态分析结果。频率变化很大,但轿厢和轿架的上下晃动的模态频率变化极小。所以可以推测,轿架的平面自由度约束方式不影响Z向的结论。
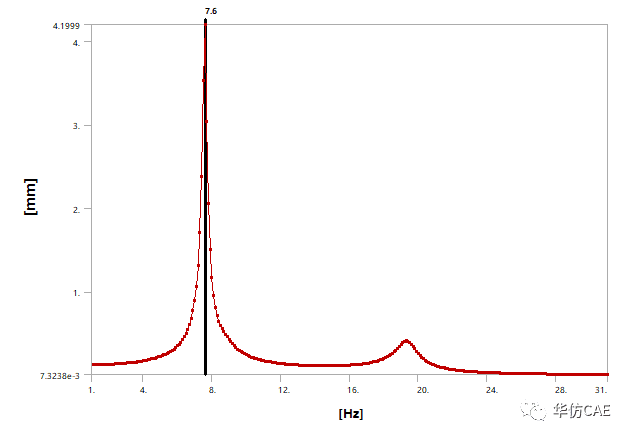
假设通过测试,判断出振动在7.6Hz有较大的幅值。本文演示使用动力吸振器抑制该振动分量。
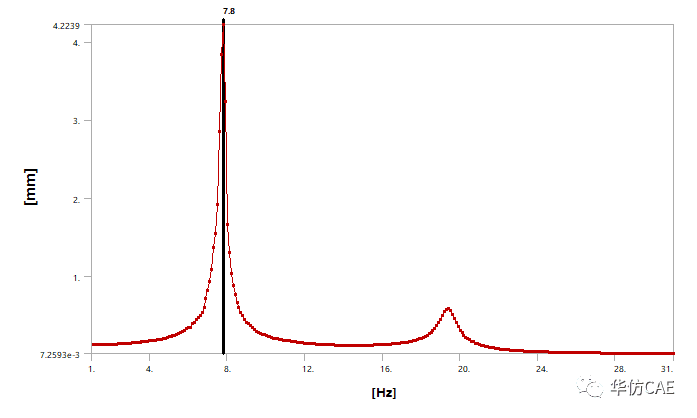
抑振前,7.6Hz对应的振动幅值为4.2mm。
设动力吸振器的质量为10kg,安装在轿架的横梁上。
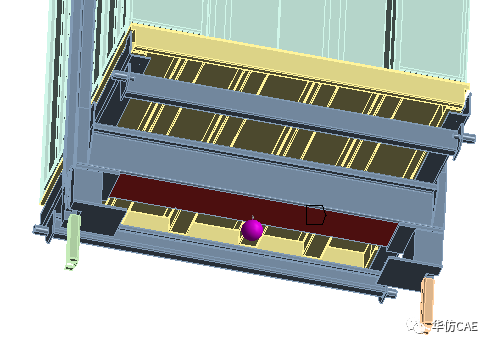
抑振后,7.3Hz对应的振动幅值为2.3mm。

设动力吸振器的质量为10kg,安装在轿厢底部。
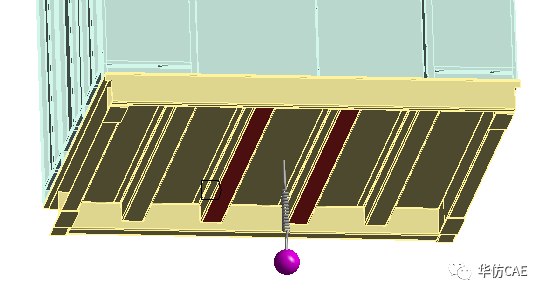
抑振后,7.1Hz对应的振动幅值为2mm。由此可见,直接安装在轿厢底部,能发挥更好的抑振效果。不过实际情况还要考虑安装空间问题。
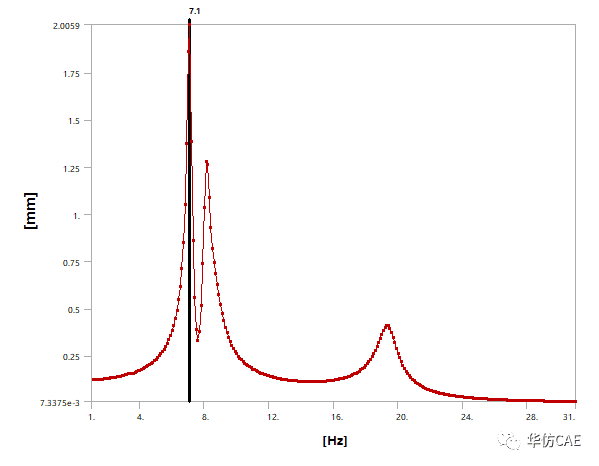
无需使用真实的轿厢模型,只需要提取钢丝绳以及隔振支座的刚度,以及反绳轮架、轿架、轿厢的质量。即可建立动力学分析模型。简单快速的完成Z向的抑振设计。

得到轿厢和轿架的Z向晃动频率。
抑振前,7.8Hz对应的振动幅值为4.2mm。
设动力吸振器的质量为10kg,安装在轿架的横梁上。抑振后,7.5Hz对应的振动幅值为2.6mm。

设动力吸振器的质量为10kg,安装在轿厢底部。抑振后,7.2Hz对应的振动幅值为2.2mm。

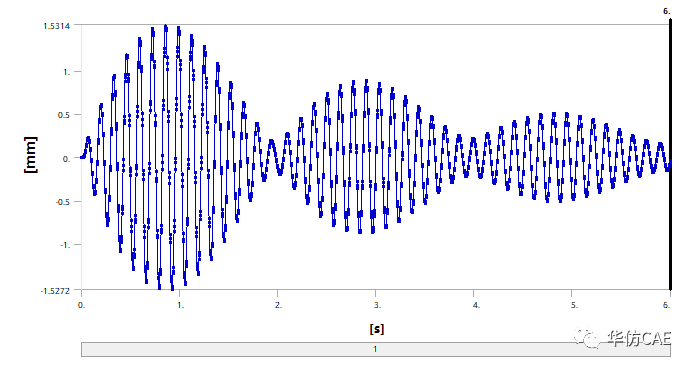
对电梯施加7.6Hz的振动激励,振动经历瞬态过程后,到达稳态共振,时域波形如下图所示。
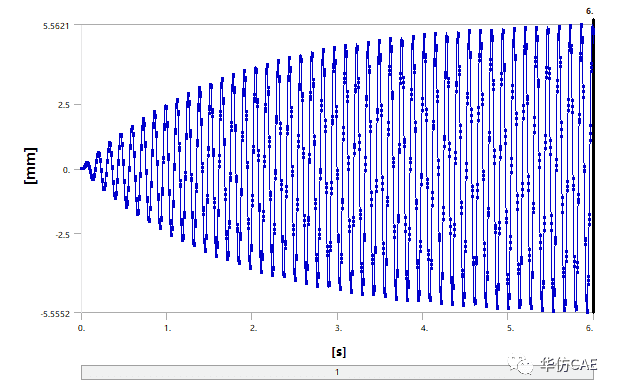
设动力吸振器的质量为10kg,安装在轿架的横梁上。

抑振后,时域波形如下图所示。
注:以下三点需要注意。
1)共振幅值和阻尼非常相关,结构的阻尼未知,可设置经验合理值;
2)本文研究的是轿厢整体晃动的相关问题,不涉及零部件共振问题;
3)真实电梯系统结构复杂,相关频率不可能和仿真分析结果完全一致,解决实际电梯问题应该将实测数据和仿真趋势相结合才能更好的解决振动问题。
来源:华仿CAE




