Simdroid 软件壳单元算法简介
Simdroid®(伏图®) 5.0版本即将发布,新版本对壳单元算法进行了比较大的更新。提前剧透一下,本文简单介绍软件中使用的各类壳单元算法以及其对应的特点。
从非线性算法的角度分类,Simdroid主要包含三类格式的壳单元,共旋坐标格式、完全拉格朗日格式以及更新的拉格朗日格式。
Corotation格式
Simdroid软件采用共旋坐标格式(corotation格式)的壳单元包括DKQ、TMQ、MITC4、Shell4_CB 等。共旋坐标格式的特点是可以将任何线性壳单元算法扩展至大转动,可以保留线性单元的优点,对于转动主导的问题有比较强的收敛性,特别适合大转动小应变分析。
共旋坐标单元的基本算法是考虑一个在单元中心随体旋转的单元坐标系,在单元坐标系下度量节点的局部平动位移,在每个节点上有一个随节点转动的坐标系,以节点坐标系和单元坐标系的偏差度量节点的局部转角。根据节点的局部位移和局部转角,调用线性单元算法形成单元局部坐标系下的刚度矩阵和节点内力向量,再将其转换到全局坐标系下。对于全局坐标系下的应力刚度也可以直接由局部坐标系下的内力向量经过变换获得,应力刚度对保证牛顿法的二阶收敛性具有极大的作用。
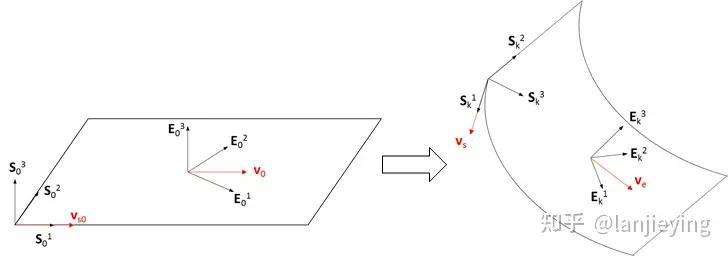
由于共旋坐标格式的限制,这类单元对于弹塑性类型的材料(率弹性材料)采用的应变/应力度量可以视为旋转的工程应变/旋转的工程应力,对于超弹性类型的材料,其采用局部坐标系下的主拉伸率和Biot主应力作为度量。
共旋坐标单元的优点包括:(1) 考虑了节点转动伪向量的准确更新和求导,对大转动具有比较强的收敛性;(2) 算法框架简单,将非线性算法和线性算法进行了解耦,可以适配不同的线性壳单元并保留线性壳单元较高精度的优点,例如对于板部分,可以兼容DKQ类型的薄板、TMQ类型的薄/厚板、以及采用ANS算法考虑厚度方向剪应变的MITC4板;对于膜部分,兼容各类非协调格式或者广义协调格式的膜算法。例如使用TMQEAS单元即为考虑增强假设应变膜算法的TMQ单元,使用TMQG8即为考虑8个内参的广义协调膜算法的TMQ单元。
该算法的主要缺点为:(1) 由于只在单元中心处构造随体坐标系,需要基于平壳假设构造壳单元,即将单元映射到一个平面上进行线性单元计算,这对于一些初始构型就是曲面的模型会损失相当一部分精度,但是如果对平壳部分的线性算法采用曲面弯矩修正技术即可保证精度。(2) 对于率弹性本构,例如一般的弹塑性材料,当弹性变形较大后该单元的假设就不再适用,计算精度会受到影响,但是对于一般的超弹性大变形问题这种单元的计算精度仍然是足够的。(3) 只在节点处满足转动的准确更新,在单元内部对转动的计算并不是李群插值和更新(也称为full SO(3) update),这一点在后文会进一步讨论。
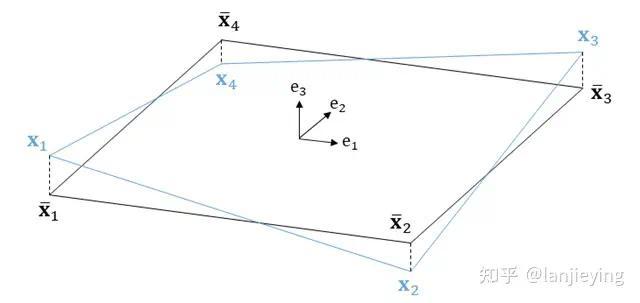
如上图所示,一般的四边形壳单元四点是不共面,可以将四个顶点向一个中间平面投影获得平面四边形单元,从而可以套用平面四边形的线性壳算法,这个平面四边形由一个面心处的共旋坐标系所确定。需要特别注意的是,必须保证节点弯矩在原始节点(非共面的四个顶点)上的平衡,否则即使是线性问题也会产生显著的误差,采用特定的曲面弯矩修正技术即可消除或减少这类误差。
Total Lagrangian格式
Simdroid软件采用完全拉格朗日格式的壳单元包括Shell4、Shell8、S4D5等。这类单元的应变/应力度量为格林应变/PK2应力,适用于大转动小应变分析,对于大部分非线性问题都有比较好的收敛性。
其中Shell4单元的厚度方向剪应变考虑ANS算法,其膜部分可以考虑EAS算法(使用Shell4EAS关键字)。所谓ANS(Assumed natural strain)算法指对两个等参方向上的横向剪应变重新进行插值,不直接选择高斯积分点的横向剪应变,而是使用边中点重新插值得到的高斯积分点的横向剪应变。采用ANS算法可以极大的减轻壳单元的剪切自锁,但对于非常薄的薄壳问题,其精度低于DKQ或TMQ等专门的薄壳算法。EAS(Enhanced assumed strain)算法指在由位移直接计算得到的应变场的基础上再附加一部分增强应变场,增强应变场一般是关于等参坐标的一次或二次项,从而附加了独立的单元内部自由度,这些单元内部自由度可以采用消去法使其从单元的层面被凝聚掉。采用EAS方法构造的单元是非协调单元,其需要满足在单元中心处计算雅可比(物理坐标对等参坐标的导数)以通过分片测试。采用EAS方法可以极大的改善单元平面内的变形能力,但其对单元的形状比较敏感,畸变的网格会显著降低单元精度。
与共旋坐标格式的壳不同,这类壳是完全的三维壳单元,其不再需要将节点映射向单元中心的平面,而是直接使用曲面坐标系计算雅可比,对于曲面问题有比较高的精度。其直接选择初始和当前的曲面坐标系(surface convected frame)作为基础来计算曲面坐标系下的格林应变。由于曲面坐标系是斜坐标系,在考虑一般的材料本构更新时,需要将应力应变等先变换到一个局部正交的笛卡尔坐标系下,完成应力更新,然后再将应力、应变、材料切线矩阵等变换回曲面坐标系下。对于超弹性材料,直接采用格林拉格朗日张量计算而无需坐标变换。
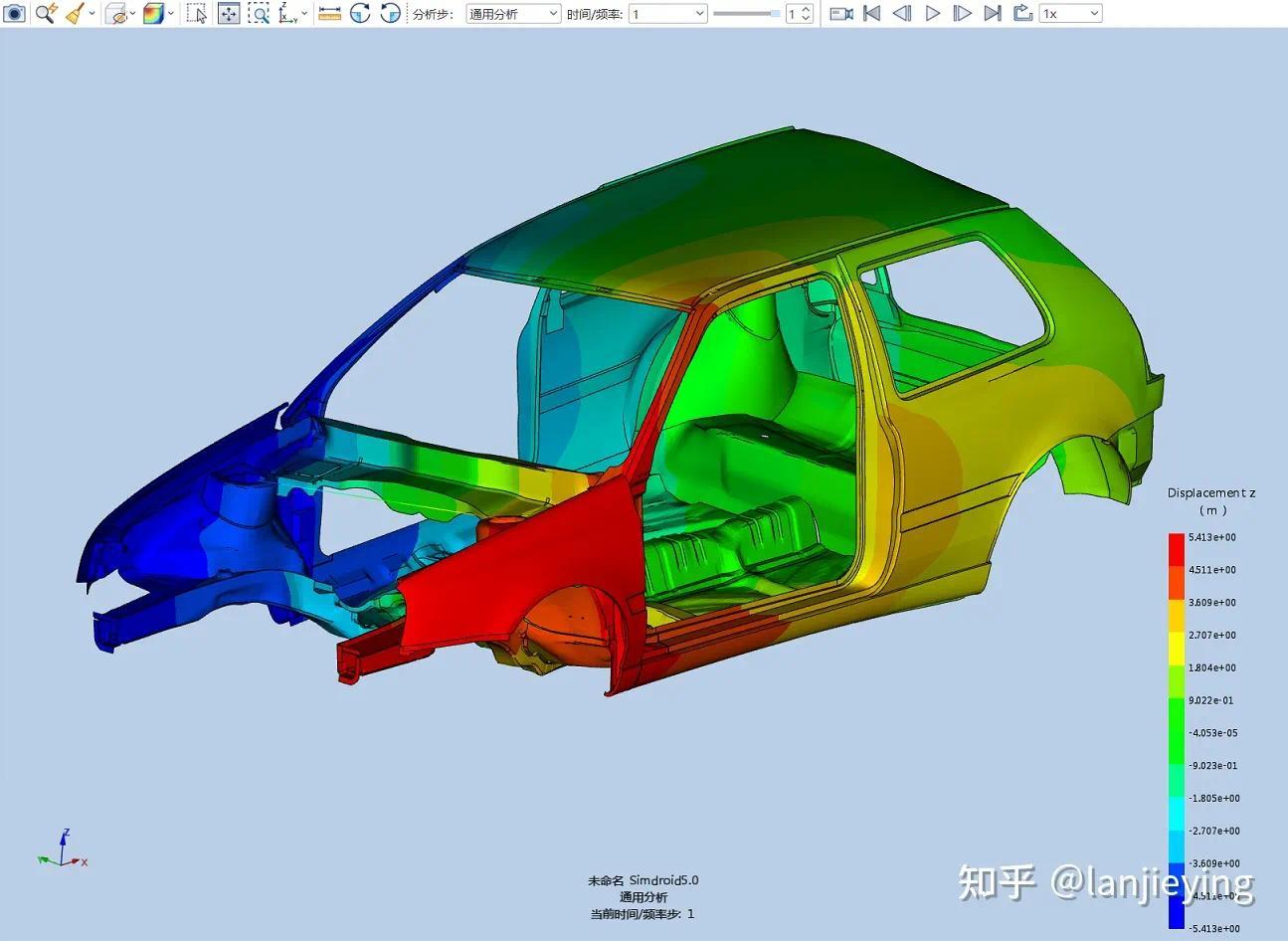
上图是一个白车身扭转工况的仿真结果,该分析是一个线性分析,采用各类单元计算相同网格的该模型结果如下表:
| 单元类型 | Z方向最大位移 |
|---|---|
| MITC4/TMQ 平面单元 | 3.6 |
| MITC4 曲面修正 | 4.7 |
| Shell4 | 4.7 |
| 商业软件1 | 4.8 |
| 商业软件2 | 5.6 |
| TMQ 曲面修正 | 5.5 |
由表结果可知,不使用曲面修正技术的平壳单元在相同网格下精度是最低的,位移仅有3.6左右;使用标准的曲面单元例如本节Shell4和商业软件1单元具有一致的精度,位移约为4.7左右,同时由于MITC4单元的横向剪切自锁的处理算法与Shell4和商业软件1是一致的,当它考虑了曲面修正后也得到了近似的结果。Nastran的壳单元在相同网格下具有最高的线性精度(即其他单元加密后可以获得相应的结果),猜测其解决薄壳的剪切自锁技术更加先进,但Simdroid软件的TMQ单元在考虑曲面修正后同样得到了与商业软件2近似的结果,即TMQ单元对横向剪切自锁的解决也相对比较合适。
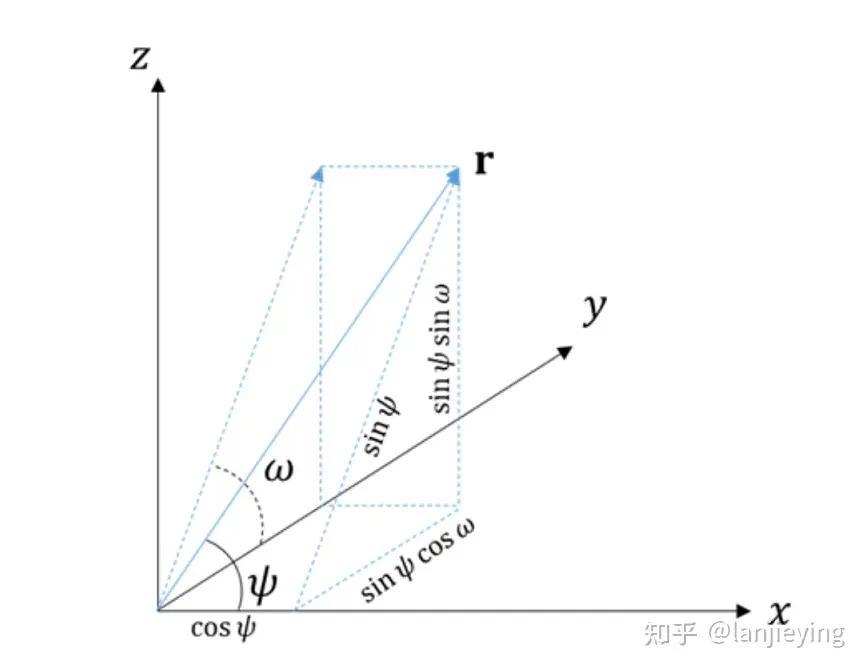
S4D5、Shell8D5等单元是5自由度壳,即每个节点包含3个平动自由度和2个转动自由度,其它壳均为6自由度壳。所有6自由度壳单元均采用节点转动伪向量作为转动的度量。S4D5为几何精确壳单元,其转动自由度为参考构型(材料构型)下的壳的法矢量的增量对应的转角自由度。Shell8D5的转动自由度为壳的当前法矢量与全局笛卡尔坐标轴的夹角,如下图的和 。5自由度壳的一个主要缺点为其对于弯矩和强制节点转动的施加点、与梁或其他6自由度单元连接点、表征几何折痕的弯折点等位置均需要特殊考虑,这在一定程度上降低了它的应用范围,目前的Simdroid求解器已经不再维护5自由度壳单元。
TL格式壳在其节点处的法矢量是精确更新的,在单元内则采用与形函数一致的插值函数对当前节点法矢量进行插值(S4D5为对法矢量的增量插值),这符合一般的连续介质单元的假设,相当于一种实体退化壳的假设,但注意其应变度量为格林应变与实体单元的变形率度量是不同的。
TL格式壳的优点是算法构造比较简单,适用于大转动小应变分析,适用于曲面模型,几何非线性的收敛速度快。缺点是对于大变形的弹塑性问题由于其采用格林应变度量,其弹性为Kirchhoff弹性,这与实体单元是不同的;此外直接对节点法矢量插值仍然不是最精确的单元转动插值方法(李群插值)。
Updated Lagrangian格式
Simdroid软件采用更新拉格朗日格式的壳单元包括HughesLiu4、HughesLiu8、S4等。经典的HughesLiu壳单元基于Thomas Hughes和Wing Kam Liu的算法构造,是一种三维连续介质单元的退化,其采用变形率和柯西应力度量,考虑柯西应力的Jaumann率。它的核心计算假设是在每个节点上考虑一组随着节点转动伪向量更新的坐标系,并在单元的每个积分点上考虑单元的层坐标系,由节点自由度更新节点坐标和节点法矢量,然后以节点当前坐标和节点法矢量计算出单元内任意一点的当前坐标,并在积分点上以当前坐标对等参坐标求导计算正交的单元层坐标系,从而可以在层坐标系内计算单元的变形梯度、速度梯度等。注意单元的层坐标系是建立在各个积分点上的,所以这类单元可以考虑曲面。Simdroid在实装这类壳单元时,与原始文献的主要区别包括:(1) 采用节点转动伪向量来表示节点转动自由度,并对其采用四元数乘法进行准确的转动更新,(2) 对于单元的一致性切线刚度的几何刚度部分,采用与三维连续介质单元一致的方式推导,确保其具有比较好的非线性收敛性。这类单元厚度方向的剪切部分采用的是选择缩减积分的方式,其精度一般比采用ANS或者TMQ等方式处理剪切自锁的壳单元差,优点是完全符合三维率形式材料的连续介质假设(考虑平面应力约束),可以用于大变形弹塑性问题。这类单元的另一个主要缺点是一致性切线刚度是基于三维连续介质力学方法形成的,这在一定程度上影响了单元的收敛速度,经过本人改善后虽然收敛性得到比较强的扩展,但仍然需要较小的单步时间增量(相对于之前的壳单元而言)。而且由于需要在每层上独立的计算B矩阵和几何刚度,它的计算量也显著的高于前文所述的壳。此外,由于它满足实体退化假设,其对单元转动的插值也不是李群插值。
最后一类S4单元,是一类考虑有限膜应变的壳单元,它同样是UL格式。其膜部分考虑在各个高斯积分点上的共旋坐标系下的对数应变(变形率)度量,在单元的积分点处构造一个随体旋转的正交的共旋坐标系,然后计算增量变形梯度以及对应的增量对数应变。节点转动自由度采用转动伪向量,与前文所有壳的核心区别是在单元内对转动伪向量的增量进行插值(李群插值),这一插值保留了法矢量的增量场非线性特征,极大的提升了算法的复杂度,但它是一种对于三维特殊正交群最为合适的插值方式,它的优点可以由后面的算例表明。
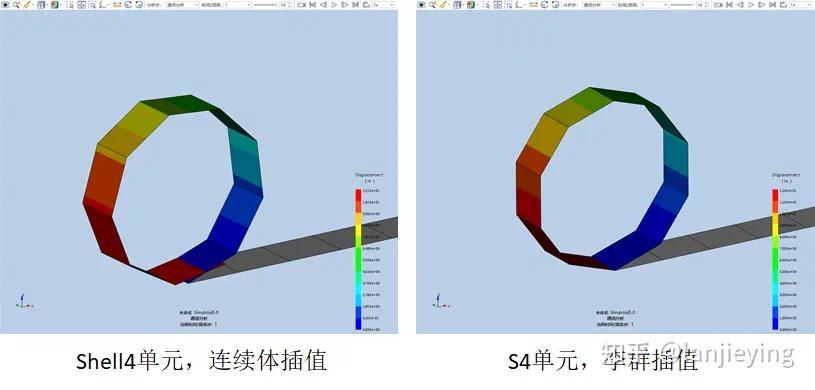 上图对比了采用Simdroid Shell4单元和Simdroid S4单元在求解悬臂梁端部受弯矩问题的结果,由于泊松比取0且施加的总弯矩恰好为2*pi*EI/L,理论上结构应该弯曲成一个正圆。可以看到采用连续体插值的Shell4单元的模型在只有10个网格时其结果有一定的误差,而采用李群插值的S4单元结果是准确的。所谓连续体插值指对节点法向矢量插值,而李群插值指对节点增量转动伪向量插值。右图的结果也是一般商业软件默认壳单元的计算结果。
上图对比了采用Simdroid Shell4单元和Simdroid S4单元在求解悬臂梁端部受弯矩问题的结果,由于泊松比取0且施加的总弯矩恰好为2*pi*EI/L,理论上结构应该弯曲成一个正圆。可以看到采用连续体插值的Shell4单元的模型在只有10个网格时其结果有一定的误差,而采用李群插值的S4单元结果是准确的。所谓连续体插值指对节点法向矢量插值,而李群插值指对节点增量转动伪向量插值。右图的结果也是一般商业软件默认壳单元的计算结果。
复合材料壳
5.0版本的Simdroid壳单元还更新了复合材料截面的计算功能,开头的演示视频即为考虑复合材料铺层后的曲壳大变形后屈曲问题的演示动画。对应的模型如下图:
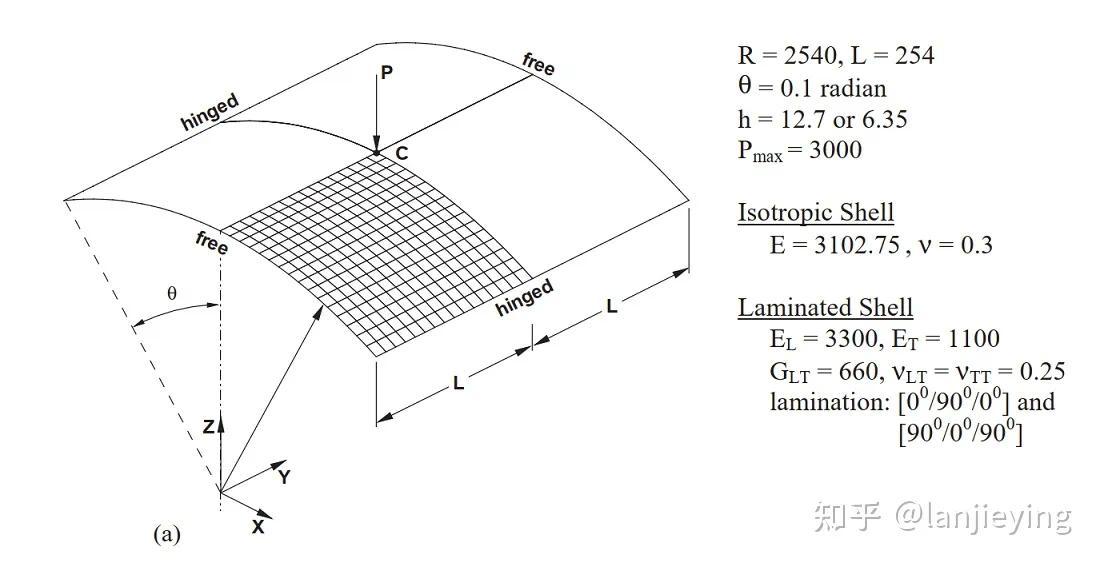
论文中采用某商业软件的S4R单元分析[0/90/0]铺层得到的荷载位移曲线结果如下图:
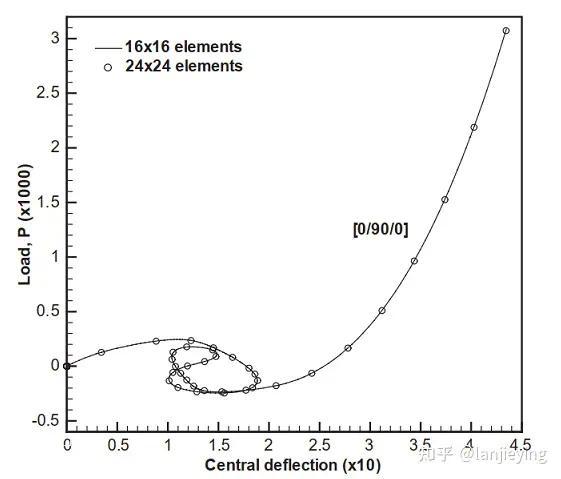
分别采用Simdroid的Shell4和S4单元计算得到的荷载位移曲线结果如下图:
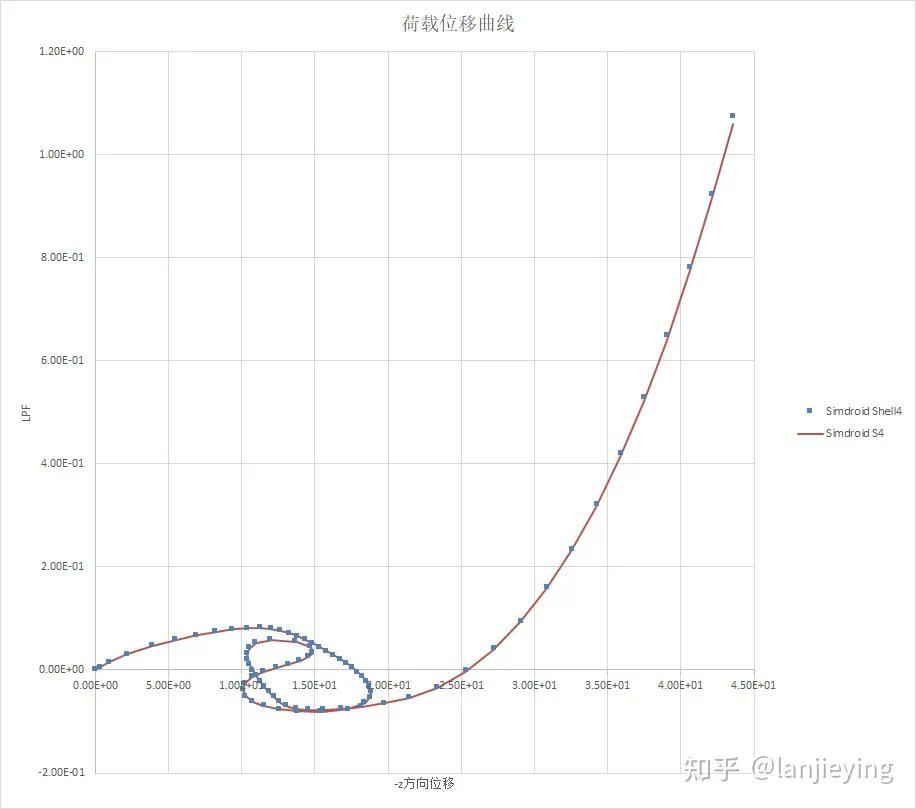
可见对于一般的大变形问题,采用连续体插值的Shell4和采用李群插值的S4单元的计算结果没有明显的偏差。




