CFD误差估计:离散误差
- 作者优秀
- 优秀教师/意见领袖/博士学历/特邀专家
- 平台推荐
- 内容稀缺

封面图采用DALL·E3生成
在分析离散误差时,需借助对细化网格上计算结果的对比来进行评估。
有关这一主题的深入探讨,可参阅第3.11.1.2节及3.9节。如先前所论,离散误差来自于对偏微分方程及其边界条件各项的近似处理。对于那些具有光滑解的问题,近似的有效性可以通过其阶次来衡量,该阶次将截断误差与网格间距之比与一个特定的幂次联系起来。若空间导数的截断误差与 成正比,则称该近似具有 阶精度。阶次并不直接等同于误差的大小,而是反映了当网格间距变化时误差的变化快慢。在相同的网格条件下,同阶近似的误差可能相差一个数量级;有时较低阶的近似在特定网格条件下可能展现出比高阶近似更小的误差。然而随着网格间距减小,高阶近似能够更快地变得更精确。运用泰勒级数展开法能够轻松地找到许多问题的近似解的阶数。然而,不同的近似方法可能会针对不同的项进行处理,因此,在整体求解过程中,阶数可能并不明显(通常它取决于方程中重要项的最不准确近似的阶数)。此外,计算机代码中算法实现的错误,也可能导致出现预期之外的阶数。因此,针对每一个问题,使用实际代码仔细检查算法的阶数至关重要。对于结构化网格中离散化误差的分析,最佳方法是在每个方向上将间距减半。然而,这种方法并不总是可行;特别是在三维情况下,这将导致节点数量增加八倍。因此,第三个网格的节点数量可能是第一个网格的 64 倍,我们可能无法承受另一个细化级别。另一方面,误差通常并非均匀分布,因此对整个网格进行细化并无必要。此外,在使用具有任意控制体积或网格的无结构网格时,由于没有局部坐标方向,网格的细化方式也会有所不同。重要的是,网格细化应当是实质性以及系统性的。例如,将一个方向上的网格节点数量从 112 增加到 128,其实并无太大意义,除非是在具有均匀误差分布和均匀网格的学术问题中;细化后的网格在每个方向上应至少比原始网格多 50% 的节点(或网格间距应至少减少 1.5 倍)。系统性细化意味着网格拓扑和网格点的相对空间密度在所有网格级别上应保持一致。网格点的不同分布可能导致离散误差发生很大变化,但节点数量并未改变。一个例子如图 8.10 所示:在非均匀网格上获得的 的结果,这种网格在靠近壁面处更加精细,其比在具有相同节点数量的均匀网格上获得的结果精确一个数量级。这两种计算结果都以相同的阶次(二阶)收敛到相同的网格无关解,但误差的大小差异达到 10 倍或更多(相对于具有相同节点数量的网格)!其他具有类似结论的例子在图 6.4、6.6 和 8.17 中给出。上述例子凸显了良好网格设计的重要性。在实际工程应用中,网格生成往往是最耗时的环节,经常生成网格都已属不易,更遑论高质量的网格。一个优秀的网格应尽可能接近正交(需注意,正交性在不同方法中有不同的含义;在有限体积法中,网格面法线与相邻网格单元中心连线之间的夹角才是关键--从这个角度看,四面体网格也可能是正交的)。在预计会出现较大截断误差的地方,网格应当更为密集--因此,网格设计者应对解的一些信息有所了解(如第 12.1.1 节所建议)。这是最为重要的标准,而使用局部细化的非结构网格最能满足这一要求。其他质量标准则取决于所采用的方法(如网格平滑度、纵横比和膨胀比等)。关于网格质量度量的更多细节将在第 12.3 节中给出。估计离散化误差的最简方法是基于理查森外推法,此法假设计算能够在足够精细的网格上进行,以实现单调收敛。(若非如此,误差可能大于预期。)因此,只有当两个最精细的网格都足够精细,且已知误差降低的阶数时,该方法才具有准确性。只要三个网格都足够精细,就可以根据以下公式计算误差阶次(详参 Roache 1994;以及 Ferziger 和 Peri ́c 1996):其中, 是网格密度增加的系数(如果网格间距减半,则 ), 表示平均间距为 的网格上的解。离散误差估计为(详见第 3.9 节):因此,当网格间距减半时,基于二阶方法的某个网格上解的误差等于该网格与前一个网格上解的差异的三分之一;对于一阶方法,误差等于前述差异。对于图8.10所示实例,当理查森外推法分别应用于均匀网格与非均匀网格时,得到的网格无关解的估计值在五个有效数字内保持一致,尽管这两种网格条件下解的误差相差一个数量级。请留意,误差可由积分量(如阻力、升力等)及物理场值计算得出,但这些量的收敛阶次可能不尽相同。对于具有光滑解的问题(例如层流),其收敛阶次通常等于理论阶次(例如2阶)。然而,在涉及复杂模型(如湍流、燃烧、两相流等)或采用开关或限流器的方案时,确定阶次可能具有一定的挑战性。然而,计算诸如阶次p或Roache(1994)称之为网格收敛指标(grid convergence index)的量并非绝对必要;仅需展示在一系列网格(最佳为三个)上计算数值的变化即可。若变化呈单调性且随着网格细化差异减小,可轻松估计网格无关解的位置。当然,在可能的情况下,应采用理查森外推法来估算网格无关解。需要指出的是,网格细化并非需要在整个域内进行。若估计结果显示某些区域的误差远小于其他区域,则可采用局部细化。这在围绕物体的流动问题中尤为正确,因为仅在物体附近和尾流中需要高分辨率。采用局部网格细化策略的方法总是比需要在整个域或网格块中细化的方法更为高效。对于非结构化网格,最粗的网格通常已涉及局部细化,然而仍需谨慎处理;如果在误差较大的地方(即大的截断误差)未对网格进行细化,那么由于误差本身受到与变量相同的传输过程(对流和扩散)的影响,网格细化效果可能并不显著。在估计离散误差时,有两个困难原因值得关注。其一是与计算湍流流体壁面函数相关的问题。详述见10.3.5.5节。在这种情况下,我们在壁面上并未指定唯一的边界条件,而是将壁面剪切应力与紧邻壁面的网格中心的流速相联系,并假定该位置位于边界层的对数范围之内。然而,在流动受到复杂壁面形状影响(即壁面法向和壁面切向存在显著梯度)时,对数定律通常并不严格适用。随着网格细化,紧邻壁面的网格中心位置会移动,从而有效地改变动量方程的边界条件;这通常会导致积分量的变化,而这些变化并不符合所使用的离散化格式的预期行为。特别是当网格细化至紧邻壁面的网格中心落入过渡层( )时,这种情况更为严重。如需使用壁面函数,应确保所有网格中靠近壁面的计算点保持在对数层范围内();另一个选择是保持紧邻壁面的棱柱层的第一层厚度对所有网格固定,以便在近壁单元格的 保持不变,壁面附近的网格仅在切向方向上进行细化。当利用网格解析边界层(所谓的低-Re方法,如在近壁单元格中心 )时,动量方程中使用无滑移条件,这使得边界条件具有唯一性。在这种情况下,积分量的变化(力、力矩、热传递等)通常更有利于使用理查森外推法进行误差估计。然而,必须确保所有近壁面单元格中的 。如果 值处于中间范围,使用所谓的全y+壁面函数比使用高Re壁面函数更好,但最好还是确保在使用壁面函数时,网格中大部分壁面的 都在 30 以上。另一个问题与所使用的网格解析几何特征有关,尤其是壁面曲率。一个典型的例子是涡轮机叶片的前缘(例如,船用螺旋桨、风扇、水或燃气轮机叶片、风或潮汐涡轮机叶片等),几何曲率通常非常高,其最大和最小压力之间的距离非常短,这需要在壁面法线和壁面切线方向上都有精细的网格。然而,商业软件中的自动网格生成工具可能无法充分解析前缘曲率,除非在网格生成过程中 特别注意(例如,通过指定前缘的网格间距,或要求曲率由圆上的某些点解析),这可能导致粗网格上前缘变得尖锐而不是圆滑。在这种情况下,网格细化实际上导致了求解区域几何形状的改变,这使得一些物理量的变化不符合预期,从而使得使用理查森外推法变得困难。因此,初始网格尽可能准确地表示求解区域的几何形状非常重要。图12.7给出了该情况的一个示例。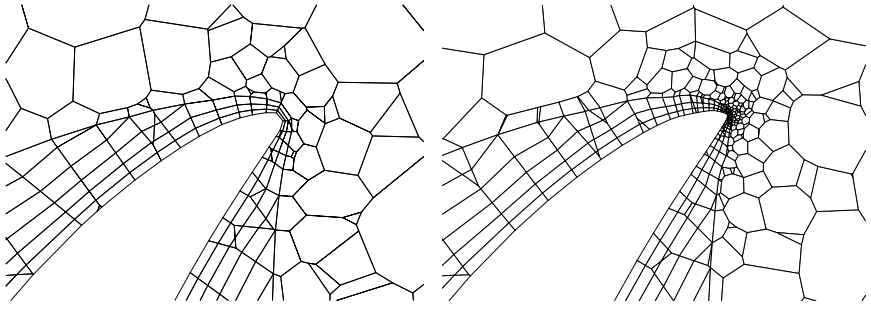
注:本文翻译自《Computional Methods for Fluid Dynamics》第4版。翻译工作由智谱清言完成,简单校对。建议看英文原版。
”
(完)
著作权归作者所有,欢迎分享,未经许可,不得转载
首次发布时间:2023-12-20
最近编辑:11月前

博士
|
教师
探讨CFD职场生活,闲谈CFD里外
获赞 2567粉丝 11306文章 734课程 27






