力学问题可分为静力学与动力学问题。而动力学问题中又分为线性动力学问题与瞬态动力学问题，线性动力学基于模态分析。瞬态问题中简单的问题可以使用模态叠加法求解，复杂的非线性动力学问题往往需要使用直接积分法求解。直接积分方法有两类，一类是LS-dyna、Autodyn等常常使用的显式积分，另一类是Ansys等软件常用的隐式积分。

对于运动问题，初中生用脚趾头想想便写出了公式：F=ma，这便是最简单的刚体运动。如果需要考虑物体的内力等，便引出了动力学公式。

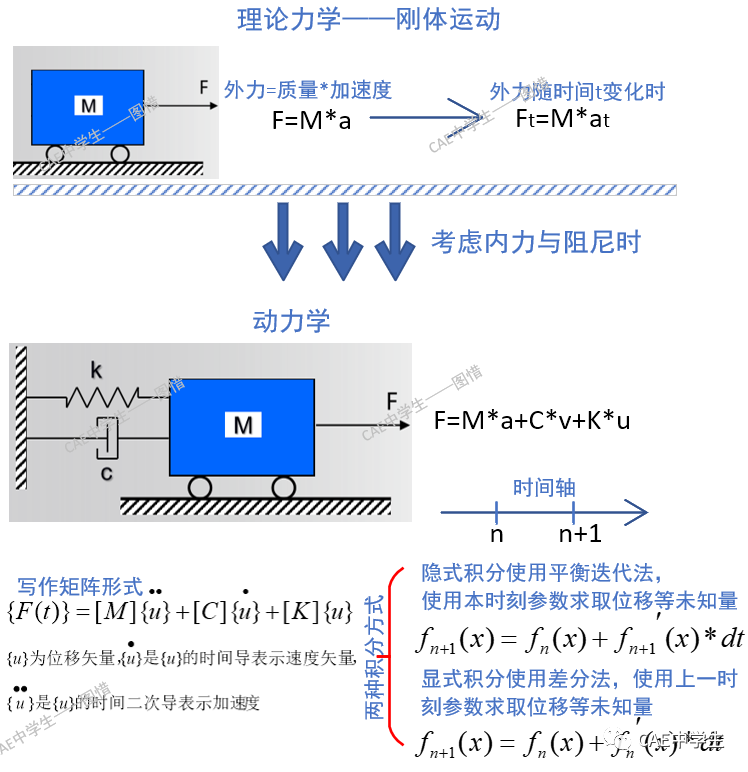
动力学往往是求位移、速度、加速度，隐式积分是使用本（n+1）时刻的参数求解未知量，显式积分是使用上一（n）时刻参数未知量，如上图。知道了这些就好比你知道了去北京要往北走，去三亚要往南走，但是你还是到不了终点，因为你只知道方向而不知道具体道路。那么就需要深入研究隐式计算与显式计算的流程与公式。

有限元求解的底层逻辑是先求解节点位移，再推导出单元应变和应力。

不管是对于隐式求解还是显式求解，当前求解步及其之前所有步的节点位移、速度、加速度都是已经被求解完成的已知量，而需要求的量便是下一时刻的节点位移量。

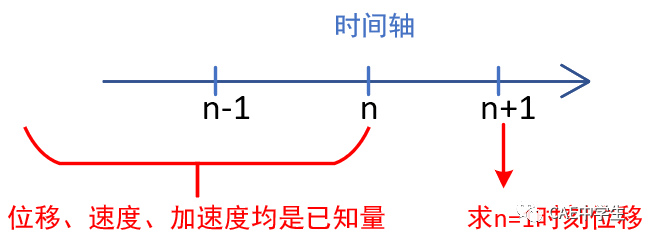
显式积分常用中心差分法，但是不是唯一方法。注意中心差分法不是有限差分法。为了简化，我们假设每一子步时间dt相同（实际软件计算中是变化步）。计算基本步骤如下图。

显式积分方法是在n时刻(即需要计算位移的上一时刻)，建立动力学方程：

由上式可以反求n时刻加速度，实际上还有沙漏阻力、接触力矢量等，所以可以将改写为

假设n-0.5→n+0.5时间段节点以a(n)加速度着匀变速运动，那么列出n+0.5时刻的节点速度公式如下。

位移计算时，假设n→n+1时间内也着匀变速运动，注意这里不关心加速度，加速度也并不是a(n)，否则节点从开始到最终都是做匀变速运动了，不符合非线性原则。此时间段节点的平均速度就是正中间n+0.5时刻的速度。

那么列出n+1时刻的节点位移公式：

由于n+1时刻的位移均有之前时刻的已知量求得，无需迭代，所以有些教材也写作函数形式：

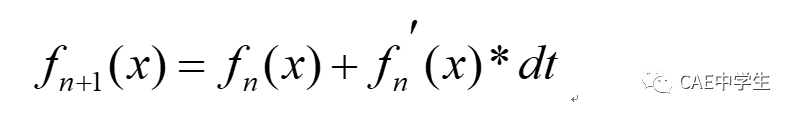
注意求位移与求速度时所使用的插值不是同一条直线，求v(n+0.5)使用的n-0.5→n+0.5时间段插值线段，斜率为a(n)；求u(n+1）使用n→n+1时间段插值线段，初始位移值u(n)，平均速度v(n+0.5)。画成几个完整时间步示意图如下。

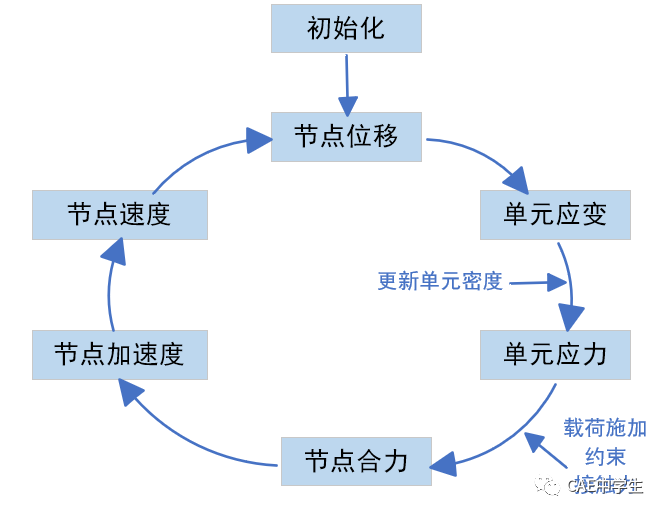
完整计算循环如下图。

以Newmark（增量迭代）方法为例。隐式积分在n+1时刻(即需要求解位移的本时刻)，建立动力学方程：

其中加速度a(n+1)与速度v(n+1)通过以下方程表示

由以上公式可知，隐式求解需要转置刚度矩阵[K]，对于线性问题，[K]为常数，无条件稳定。对于非线性问题，通过牛顿拉夫逊（Newton—raphson）方法进行一系列逼近来获取。对于复杂模型，刚度的转置过程消耗内存与时间较多。

显式积分无需检查收敛性，每一时间步开始的值由上一时刻确定，每一时间步求解一次线段斜率。

隐式积分也是在每一时间步开始时刻获得方程的切线斜率，但是每一迭代步都需要检查收敛容差。

如下图，以只设置1个子步为例，在牛顿拉夫逊方法中，第一次迭代，施加总载荷Fa。得到位移结果x1。根据位移，算出内力F1 。如果|Fa-F1|＞容差值[R]，系统不平衡。因此，根据当前的条件，计算新的刚度矩阵（虚线的斜率）。直到|Fa-F1|≤[R]。在下图例子之中，四次迭代之后，系统达到平衡，求解收敛。

由于显式积分无收敛性检查，即不需要平衡迭代，但是为了计算的稳定性和准确性，时间步长必须小于应力波（声波）在单元中的传播时间，即显式求解的准确度严重依赖于时间步长，时间步长又严重依赖单元尺寸与声速。

隐式积分对线性问题是无条件稳定的，甚至允许只设置一个时间步。隐式积分对非线性问题只要保证收敛的情况下，无论设置多长的时间步，结果都是稳定准确的；由于每一步都需要进行一次或多次平衡迭代，所以需要使用较小的时间步长保证收敛。但是总体来说，隐式计算的时间步通常比显式积分时间步大几个数量级。

如下示意图，非线性问题中，隐式求解使用较大的时间步也能保证结果稳定（准确）。而显式求解使用较大时间步后导致计算结果偏移较大，而减小子步时间后，结果准确度提高。

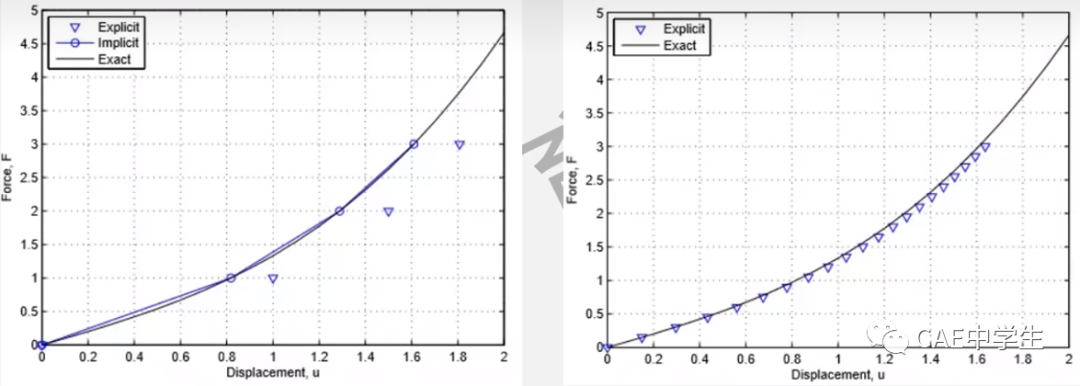
所以显式算法常用于毫秒级的问题，如爆炸、碰撞等，当然也能用于成型等准静态问题，而隐式算法常用于秒级以上的静态或准静态问题。

显式问题往往需要更高频率的CPU以保证计算效率，而对内存要求不高，而隐式算法中由于需要对刚度求逆并进行平衡迭代，需要消耗很多时间，往往需要较大的内存，对CPU的要求反而没那么高。

[2]《Ansys Workbench结构分析理论详解与高级应用》——尚晓江等

[3]《TrueGrid和LS-DYNA动力学数值计算详解》——辛春亮等

[4]《LS-DYNA基础入门教程》视频——水哥

[5]《ANSYS_WB_LS-DYNA - Explicit Dynamics Basics》——培训手册内容