热塑膜开孔对放疗头部固定效果的有限元研究

摘    要：

【目的】放射治疗是肿瘤治疗的重要方法之一，临床中常采用热塑膜来固定患者体 位，精准的体 位固定是保证治疗可重复性和准确性的重要因素。【方法】通过一名头部肿瘤患者的CT图像，建立了2种不同开孔的热塑膜有限元模型。通过拉伸实验测定了热塑膜的材料性能，模拟了3种不同厚度的热塑膜模型在受载荷条件下的位移和应力响应。【结果】不开孔模型的位移量最大，嘴部开孔模型的位移量最小；面部全开孔模型的应力最大，不开孔模型的应力最小。【结论】为研究热塑膜固定效果提供研究思路和参考，也为将来患者的个性化定位治疗提供一定的参考。

关键词：放射治疗;热塑膜;有限元分析;

癌症已成为全球主要疾病致死原因之一，受到全世界政府和组织的关注[1,2,3]。在中国，癌症人数多，患病比例相较世界平均水平更高，癌症负担持续增长。据世界卫生组织统计，全球头部肿瘤的发病率很高，约占人类恶性肿瘤的6%～8%[4,5].治疗癌症的方法主要有手术治疗、化学治疗和放射治疗[6]。放射治疗使用人工或天然射线对病灶实施“无创性”治疗，相较于手术和化学治疗，放射治疗有许多的优势，也成为了许多肿瘤患者的重要治疗手段之一[7]。近年来，随着生物医学工程、放射物理学、放射生物学、计算机科学等多学科的不断发展，放射治疗进一步提高了治疗的精准化和个性化[8,9,10,11]。

头部器官众多，治疗时需保证射线照射位置的准确性，以免伤及其他组织和器官。在放疗疗程中，大多数患者通常需要进行20～30次射线照射，确保每次治疗时患者体 位的重复性至关重要，也是保证治疗效果和治疗准确性的重要环节。放射治疗中常采用一种由高分子材料组成的具有低温热塑记忆性的膜(以下简称热塑膜)来固定患者体 位[12]。这种膜在70 ℃时软化，将软化的膜覆盖在患者身体表面，通过卡扣与床板联结，冷却后完成固定。但是在临床中常常会遇到一些头部有伤口或需要进行鼻饲插管等情况的患者，这时需要对热塑膜开孔，以保证治疗顺利进行。除此之外，一些有幽闭恐惧症的患者在头部覆盖热塑膜后会产生恐惧心理，导致身体不自主地运动，严重影响固定效果和治疗效果。在面部进行开孔，尤其在眼部和口鼻位置开孔将极大地缓解患者的恐惧和紧张心理。然而，如热塑膜开孔过大，患者会不自主地运动，可能导致热塑膜的动度过大，造成放疗区域的偏差，甚至酿成医疗事故；如开孔过小，患者的舒适性得不到明显改善。目前对于热塑膜开孔部位、开口大小对固定效果影响的相关研究鲜少，还缺乏直观、量化的评估。LOJA et al[13]通过对标准头部模型进行CT扫描，重构出3种开孔模式的热塑膜模型，模拟了不同载荷条件下，热塑膜产生的应力分布和位移分布。但是患者个体差异较大，采用理想模型模拟误差较大。其次热塑膜的性能对模拟结果的影响较大，尚未有文献对热塑膜材料性能进行测量。基于此，本文通过建立患者个性化模型，设计不同开口模式，来模拟不同开孔模式对热塑膜固定效果的影响。本研究的意义在于提出一种个性化建模方法，用以研究固定膜开孔方式对固定效果的影响，为热塑膜开口等相关问题的研究提供思路。

1 方法

1.1 数据采集

选取一例山西白求恩医院肿瘤中心确诊的脑胶质瘤患者头部CT图像。该患者为女性，35岁，于2023年4月19日入院，经过完善相关检查，使用飞利浦16排大孔径定位Brilliance Bigbore CT对患者头部行层厚为2 mm的CT扫描，并计划给予TOMO放疗。本研究得到山西白求恩医院伦理委员会批准通过(YXLL-2022-127).

1.2 建立模型

对患者头面部进行CT扫描，使用CT自带的重建系统对图像进行薄层重建。在MIMICS软件中生成患者的头部几何模型并导出为STL格式，将STL格式的模型导入3-MATIC软件中进行Laplacian平滑处理。Laplacian平滑通过迭代将网格的每个顶点移向其周围邻域重心的位置，拉普拉斯坐标的表示形式如式(1)所示。

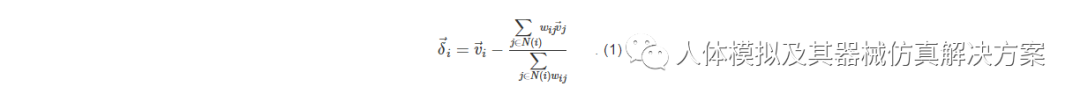
式中：N(i)为顶点vi的邻点集 合，wij表示顶点vi的第j个邻居的权重。如果权重都是1,那么这个公式(1)就可简化为取顶点与其邻居的平均值之差：

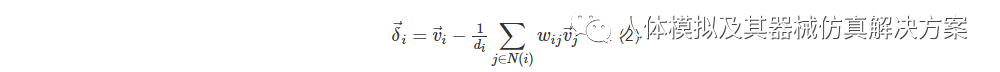
其中，di是顶点vi的邻点数目。这种选择所有相邻节点的权重相等的方案被称为伞形加权方案。通过HYPERMESH 2019软件中几何逆向提取功能，以固定膜三角网格模型作为输入，逆向提取得到曲面几何模型，划分网格，设计如图1所示的3种开孔模型，导出为INP文件。

1.3 测定热塑膜性能

通过广州科莱瑞迪医疗器材股份有限公司获取热塑膜材料，根据国标GB/T 1040.2-2022制备5组标准拉伸试验样品。样品尺寸和形状如图2所示。试样长度为75 mm, 宽度12.5 mm, 标距段长度25 mm, 标距段宽度4 mm, 试样厚度为2 mm.在万能试验机(Instron 5544)上进行准静态拉伸测试，拉伸速率设定为0.5 mm/min.试样拉伸如图3所示。由于热塑膜在拉伸过程中标距段有大变形，因此测得的工程应力σe和工程应变εe并非材料真实应力σt和真实应变εt,需通过以下公式转换：

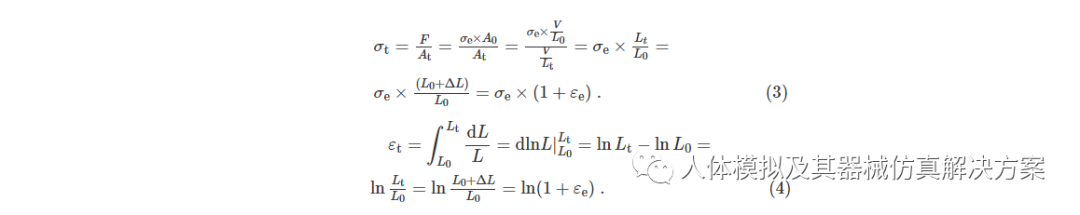
式中：F为拉力，A0和At分别为标距段初始截面积和真实截面积，L0和Lt分别为初始标距段长度和真实标距段长度，L为试样长度，V为标距段体积。在屈服及随后的塑性流动期间，材料流动引起的体积改变可忽略不计，因为长度增加的影响被横截面面积的减小所抵消。在颈缩前，应变沿整个试样长度仍旧是相同的。根据转换后的真实应力应变曲线拟合计算材料弹性模量，并且通过测量线弹性阶段热塑膜标距段的尺寸计算泊松比，结果取5组数据的平均值。

1.4 有限元模拟

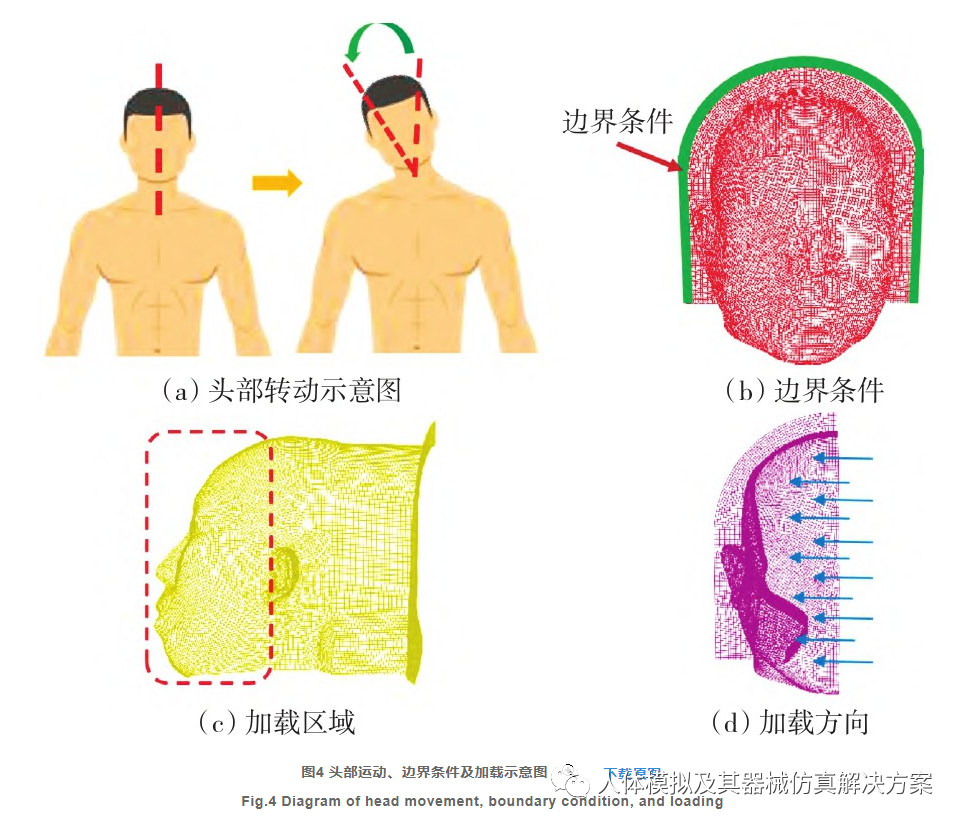
由于热塑膜覆盖在人体表面冷却成型，热塑膜冷却后形态大致与人体表面近似，因此将CT获取的人体表面形态视为热塑膜最终成型形态。实际治疗中热塑膜覆盖在人体表面时会产生摩擦，本研究中忽略了摩擦对计算结果的影响。由于人头部在放射治疗过程中产生的动度是很难准确测量到的，本文选择ALMOSNINO et al[14]通过传感器检测运动员头部向右弯曲时产生的力，约为157.2 N.通过有限元商业软件Abaqus 2020进行计算。模拟头部向右弯曲施加均布载荷于面罩内部右侧位置。在治疗时，热塑膜边缘固定于治疗床上，因此固定模型边缘处，边缘转角和位移均设定为0.头部转动示意图如图4(a)所示，边界条件如图4(b)所示，固定绿色线部分。均布载荷加载区域如图4(c)虚线中范围，载荷方向如图4(d)所示，从面罩内侧指向外侧，载荷大小为0.012 MPa.模型单元主要以六面体划分，部分区域采用四面体单元。进行静力学分析计算位移和应力分布。为保证计算收敛性，对网格密度进行了稳定性和精度验证。临床中有多种厚度的热塑膜，本文选用热塑膜厚度为3 mm、4 mm和5 mm进行计算分析。

2 结果

2.1 热塑膜弹性模量

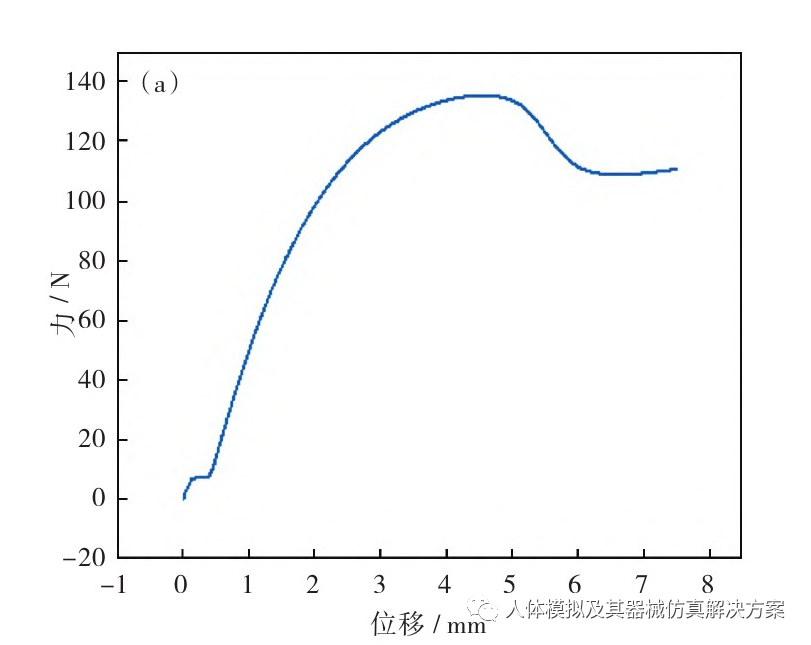
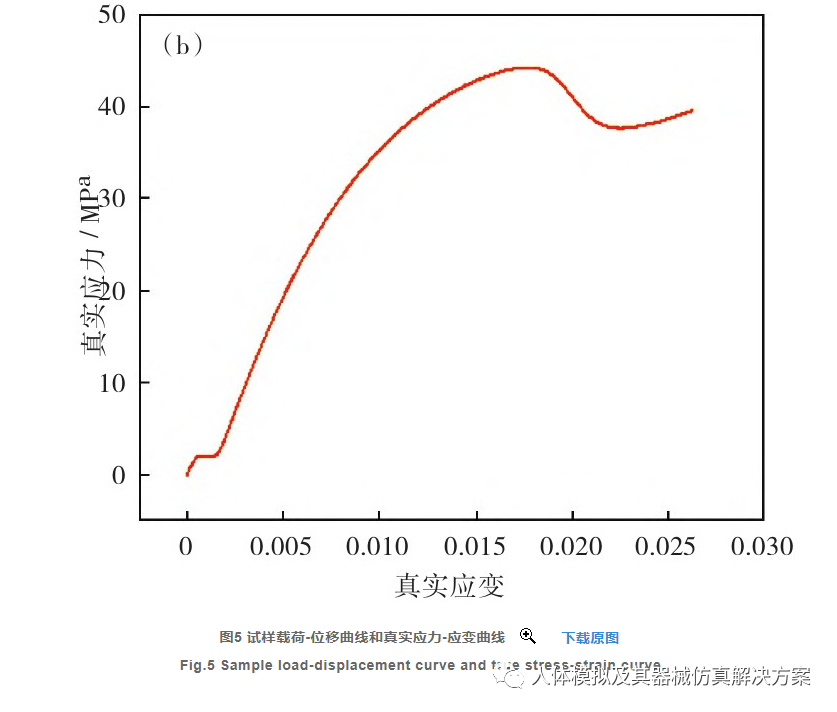
通过热塑膜拉伸实验得到的工程应力-应变曲线换算为真实应力-应变曲线，取线性曲线部分计算得到曲线斜率即为弹性模量。5组弹性模量值分别为3.90 GPa、4.70 GPa、4.20 GPa、4.50 GPa、4.95 GPa, 取均值为4.45 GPa.以弹性模量值为4.20 GPa的试样为例，图5为该试样拉伸实验的载荷-位移曲线和真实应力-应变曲线。

2.2 位移和应力分布

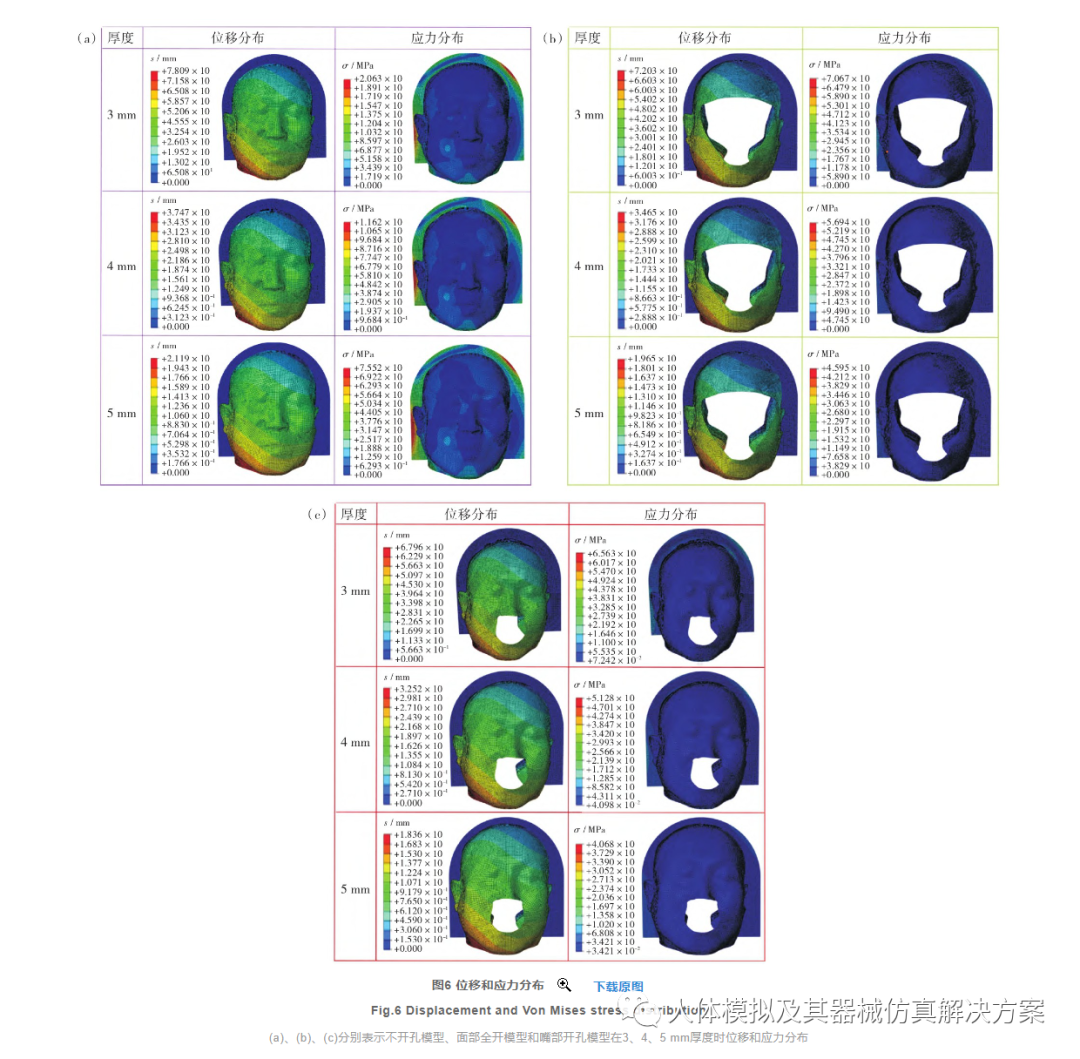
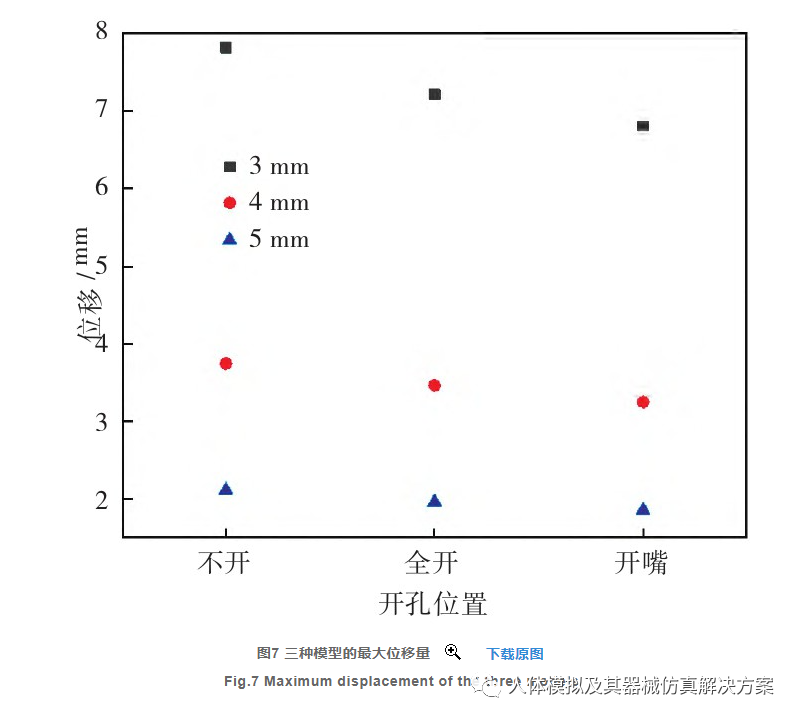
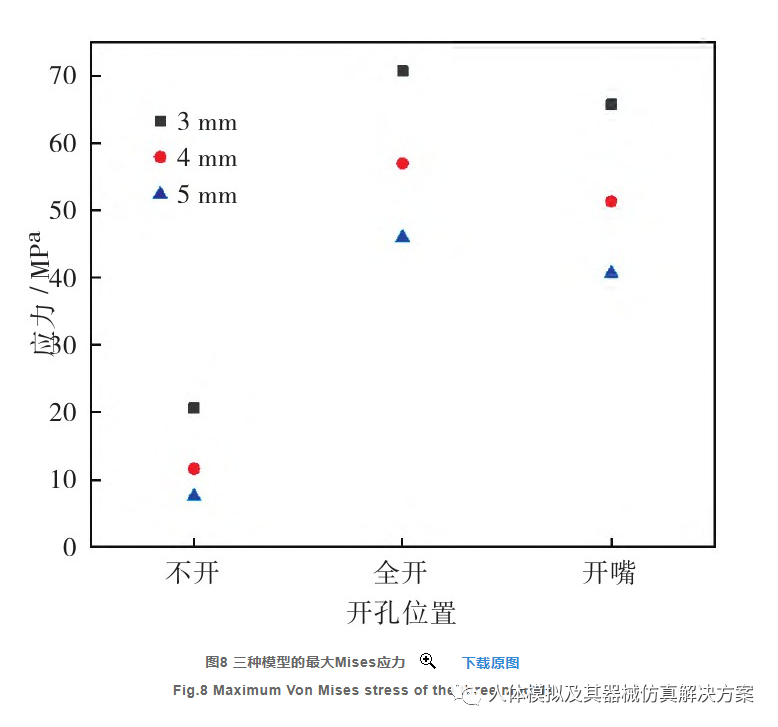
将3个模型均模拟头部右侧弯曲时的状态，得到相应的应力和位移分布。每种模型模拟3种膜厚度，共9组结果。图6展示了3种模型在不同厚度情况下受力时产生的位移和应力。由于加载的均布载荷在模型的右侧，因此从位移云图中可看出位移和应力分布均不对称，位移较大的位置都出现在模型的右下角区域。图6(a)不开孔模型在3 mm、4 mm和5 mm厚度时最大位移量分别为7.809 mm、3.747 mm和2.119 mm; 最大Mises应力分别为20.63 MPa、11.62 MPa和7.55 MPa.图6(b)面部全开模型在3 mm、4 mm和5 mm厚度时最大位移量分别为7.203 mm、3.465 mm和1.965 mm; 最大Mises应力分别为70.67 MPa、56.94 MPa和45.95 MPa.图6(c)嘴部开孔模型在3 mm、4 mm和5 mm厚度时最大位移量分别为6.796 mm、3.252 mm和1.836 mm; 最大Mises应力分别为65.63 MPa、51.28 MPa和40.68 MPa.分析每种开孔方式的应力分布可看出，3种厚度的热塑膜最大应力出现的位置均在热塑膜与床板固定位置附近，也就是膜的边界固定区域。图7和图8分别为3种模型在不同厚度时的最大位移对比图和最大Mises应力对比图。从位移图中可看出，3种模型的最大位移量均随着膜厚度增加而降低；未开孔模型的位移量最大，嘴部开孔模型的位移量最小。对于模型的最大应力，3种模型的最大应力也均随着膜的厚度增加而减小；但应力最大的模型是全开孔模型，其次是嘴部开孔模型，应力最小的是不开孔模型。

3 讨论

热塑膜本身具有弹塑性、超弹性属性，但是本文模拟头部转动的力较小，材料产生的变形为小变形，在小变形阶段可以近似将材料认为是线弹性材料。此外，超弹性材料在有限元计算中需要待定的参数较多，通过应力-应变曲线拟合出材料参数有一定的困难，极大地增加了计算成本，因此本文将热塑膜近似视为线弹性材料。LOJA et al[13]选用的材料参数源自PMMA的实验数据，其测得的弹性模量范围为2.10～4.33 GPa, 但临床医用热塑膜的成分除了PMMA以外，还有固体石蜡、低密度聚乙烯、交联聚维酮以及其他有机成分，因此用PMMA的材料属性并不能等同于热塑膜的材料性能。本文计算得到热塑膜的弹性模量为4.45 GPa, 相较于文献[13]中仅用PMMA测得的结果更准确。此外，不同厂家生产制备热塑膜的材料成分配比各有差异，膜的软化温度、硬度均不相同，弹性模量也会有所不同，采用不同弹性模量计算出的模型最大位移和最大应力也会不同，本文只选用了一个厂家材料进行了性能测量，因此本文计算出的位移量和应力仅可作为参考值。

有限元模型计算的位移量一定程度上反映了热塑膜的固定效果。从图7的位移数据中可以看出，未开孔的模型位移量是最大的，其次是模型开孔面积最大的模型。这反映了在头部向右侧弯的受力工况下，并非开孔面积越大，位移量就越大，开孔面积的大小和位移量没有必然对应关系，热塑膜产生的最大位移量反映的是固定效果。不开口模型受力时形变均匀，而嘴部开口模型变形不均匀，导致不开口模型的最大变形量大于开口模型的最大变形量。这提示应关注重点区域的变形量，对于不同的放射治疗位置，应具体分析目标区域的变形量。应力分布与开孔面积相关，开孔面积越大的模型，最大应力也越大；而Von Mises应力与热塑膜破坏的风险相关，也即开孔面积越大，热塑膜发生破坏的风险越高(如图8所示)。

4 结论

本文采用特定模型分析了头部转动时产生的力学响应，仅仅反映了不同开孔位置对固定效果的影响程度，只能做半定量或定性分析，与临床上患者治疗过程中产生的摆位误差的验证关系也有待进一步研究。此外，在临床实践中，每个患者在治疗时身体产生不自主运动的差异较大，患者平躺在治疗床上产生不自主运动的力很难准确测量，本文采用文献[14]中运动员在转动头部的情况下测得的最大力进行仿真计算，但这个力的值和每个患者躺在治疗床上产生的力并不相等，且远大于患者治疗时头部侧弯所产生的力，这是作为一种极端情况考虑，计算的结果也并非患者实际产生的位移和应力值。LOJA et al[13]通过建立标准头部模型，模拟与本文类似的颈部弯曲，考虑极端情况施加152 N的力，计算所得位移量范围为1.10～8.92 mm, 与本文计算的位移范围1.86～7.81 mm接近，因此认为本文计算的位移范围是在合理范围内的。目前医院使用的头部热塑固定膜常采用图1(a)所示的多孔状材料，而不是本文模型所用的实心材料，这是因为多孔材料在建模划分网格时容易造成网格数量过多，计算成本过大，且网孔边缘处网格质量较差，造成计算难以收敛，更精确的有限元几何模型有待进一步研究。

本文通过建立患者个性化有限元计算模型，分析了头部转动时热塑固定膜产生的位移和应力分布。本研究为研究热塑膜固定效果提供研究思路和参考，也为将来个性化医疗提供一定的参考。

参考文献：[1]孟乔宇,孟莹,庞国宝等.热塑膜开孔对放疗头部固定效果的有限元研究[J].太原理工大学学报,2023,54(05):934-940.DOI:10.16355/j.tyut.1007-9432.2023.05.022.

免责说明：文章仅供交流学习，版权归原作者所有。如有涉及版权，请联系删除！