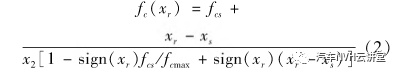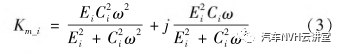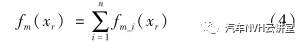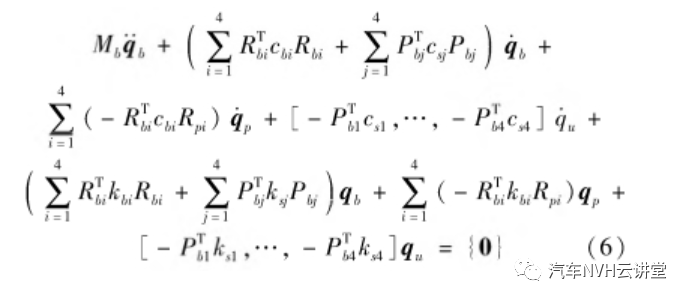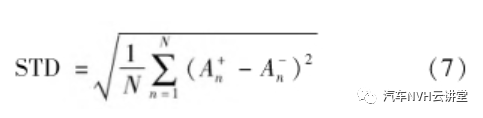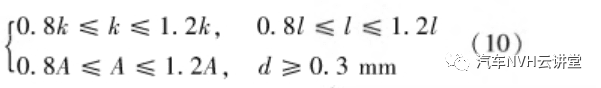解耦液压悬置建模及时域仿真研究
摘要：在分析解耦液压悬置的内部结构和考虑橡胶、液压模块非线性特性基础上，建立了能表征解耦液压悬置动态特性的物理模型，计算分析了解耦液压悬置的动态特性，研究了解耦盘及惯性通道在不同振幅条件下对悬置动态特性的影响。试验结果表明：所建物理模型能够较好的表征解耦液压悬置的幅变，频变特性。建立了包含解耦液压悬置的整车13自由度动力学模型，仿真计算了路面激励工况下系统的时域响应，并通过实车进行验证。最后，以抑制车辆过减速带衰减动力总成振动为目标给出了液压悬置的优化方案。结果表明：仿真计算出的发动机侧悬置和变速箱侧悬置振动加速度峰峰值与试验结果分别仅相差4.5%和12%，整车13自由度动力学模型得到了较好的验证；优化后的解耦液压悬置处振动加速度峰峰值衰减到初始状态的40%，优化效果明显。该研究方法为解耦液压悬置的设计、匹配提供参考。1 解耦液压悬置建模
解耦液压悬置结构见图1。从图1可以看出：橡胶主簧通过硫化与金属外罩连接并与解耦盘组成上液室。当悬置受到来自发动机或者车身的振动激励时，橡胶产生变形，上液室体积发生变化，将液体通过惯性通道以及解耦盘的通道挤压到由解耦盘与橡胶皮碗组成的下液室。在这个过程中，液体在流道中的共振、解耦膜片在解耦盘间振动和橡胶的非线性特性共同导致解耦液压悬置的幅变以及频变特性。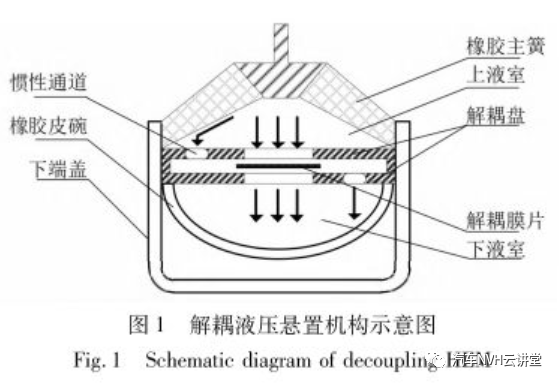
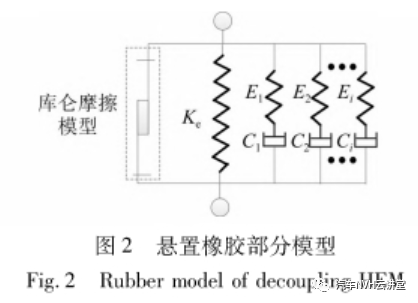
建立橡胶动态模型时，必须考虑其动态特性的频率以及幅值相关性，建立的模型见图2。图2中库仑摩擦模型表征橡胶的幅变特性；多个并联的Maxwell单元模型表征橡胶的黏弹特性。根据所建立的模型，力fr与位移激励xr的关系可以用式(1)表达式中：fe为线弹性力；fc为摩擦力；fm为黏弹性力。库仑摩擦模型描述的是一种具有摩擦力特性的激励位移与响应的关系，主要表征橡胶的幅变特性。其力与位移的关系可表示为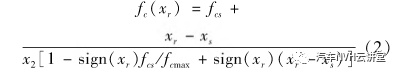
式中：fcmax表示最大摩擦力；x2表示达到fcmax/2时的位移量，反映了摩擦力随位移增加的变化速度；fcs和xs各表示初始状态下的力与位移。Maxwell单元是指将一个线性的弹簧与一个线性阻尼串联以表征橡胶的黏弹性特性。具体模型中Maxwell单元数量需要根据试验结果确定。对于第i个单元的等效动刚度为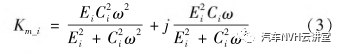
式中：Km_i为第i个Maxwell单元的等效动刚度；Ei和Ci分别为这个单元的刚度以及阻尼；ω为系统的激励频率。则该单元的力fm_i(xr)=Km_ixr；整个Maxwell模型的力与位移关系为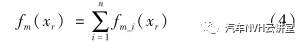
式(2)～(4)中相关参数的试验获取方法详见文献[4,17]。1.2 液压构件物理建模
由于没有较为准确的数学模型能够同时表征惯性通道以及解耦盘内液体的流动，文中通过物理建模的方法建立悬置的液压部分模型。利用两个带活塞的液压缸来表征悬置的上、下液室；活塞的运动代表了悬置受载产生的变形。液压缸通过三通管道分别与惯性通道、解耦盘连接；利用一个质量块以及非线性弹簧表征解耦膜片在悬置受载时在解耦盘间的运动，所建模型见图3。部分参数见表1。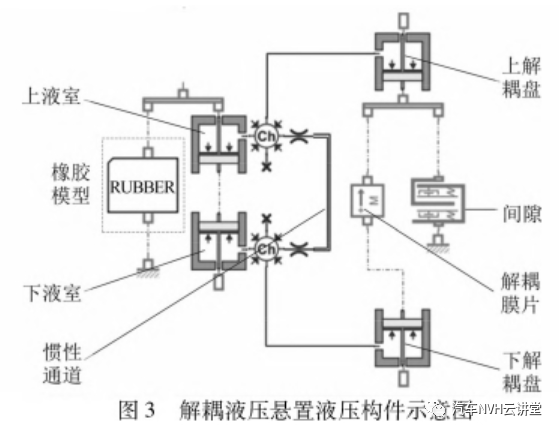
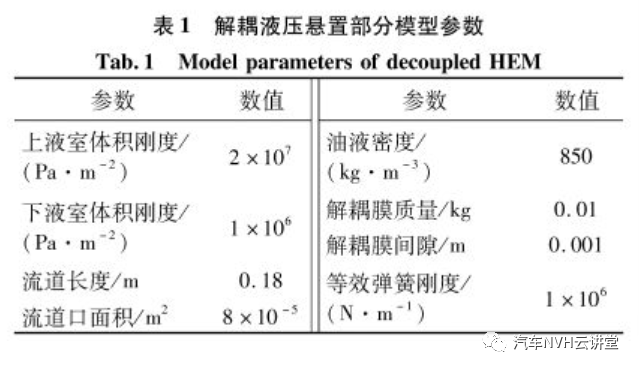
1.3 动态特性分析
在AMESim软件中搭建图3中的模型。将模型一端固定，一端施加一个正弦扫频激励，读取力与位移的关系，计算得到解耦液压悬置的动刚度和滞后角，仿真结果见图4和图5。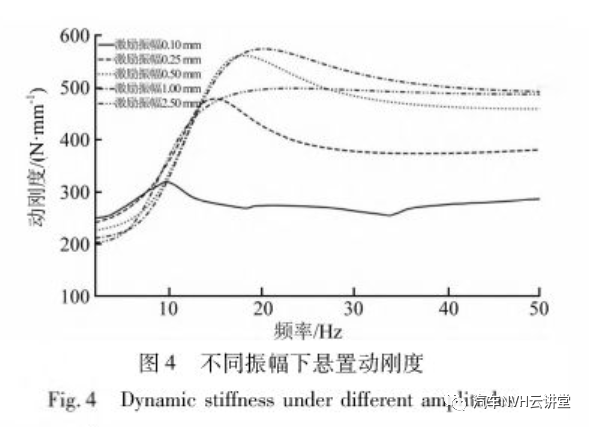
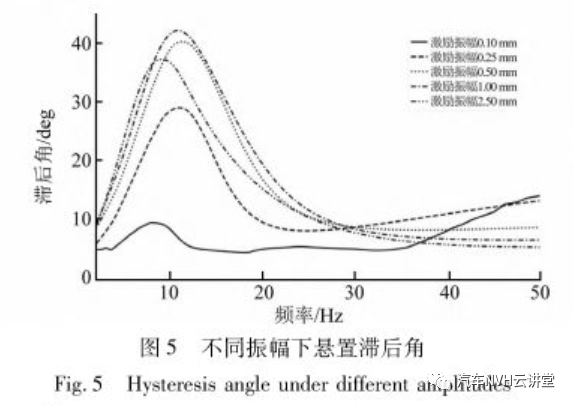
从图5可知：当激励幅值为0.1 mm时，随着激励频率的增加，动刚度、滞后角整体没有什么变化，仅在10 Hz附近有一个小凸峰。随着激励幅值增加，悬置的动刚度在10 Hz附近突然增大，对应的滞后角在此处也出现明显峰值；说明此处液室内的液体在惯性通道内产生了共振。动刚度和滞后角的峰值开始随着激励振幅逐渐增大，但激励幅值大于1 mm后，峰值随激励幅值增大而减小。对于非解耦的液压悬置，当激励幅值减小时，流体的阻尼效应越明显，动刚度和滞后角峰值会随激励幅值减小而不断增大。发动机产生的激励都是高频小振幅激励，非解耦液压悬置动刚度高，不利于振动的衰减。解耦液压悬置通过解耦膜在解耦盘间的运动，可以有效降低高频小幅值时的动刚度。在较大振幅下，解耦液压悬置的橡胶主簧变形量较大，大量的液体通过惯性通道在上，下液室之间往复流动，产生较大的黏滞阻尼和较高的动刚度。当振幅较小时，橡胶变形量小，液体流动较少，解耦膜片的弹性变形及其在解耦盘间的运动可使这部分液体流过而不会导致解耦膜片与解耦盘贴合，致使惯性通道中几乎没有液体流动，使悬置呈现低刚度和小阻尼特性。为了研究在不同振幅下悬置内部液体的流动情况，将解耦液压悬置下端固定，上端给一个激励频率25 Hz的恒定幅值激励，图6和图7分别表示激励振幅为0.1 mm和1 mm条件下液室内部液体流动情况。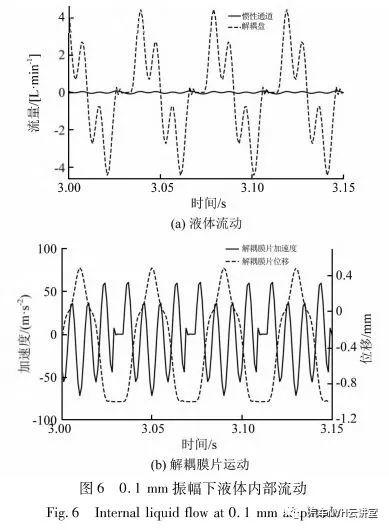
从图6可知，在小振幅条件下(0.1 mm)，液体几乎完全通过解耦盘在上、下液室内流动，而惯性通道内几乎没有液体通过。解耦膜片在解耦盘间往复振动，而没有与解耦盘贴合。此时由于惯性通道内几乎没有液体流动，液体在流道内的共振很小，对悬置的动态特性几乎没有影响；此时，悬置的动态特性基本由橡胶主簧提供，整个零件表征出的动刚度和滞后角也与橡胶悬置类似；解耦液压悬置在小振幅激励下表现出了低刚度，小阻尼的特性。从图7中可以看出，在大振幅条件下(1 mm)，惯性通道内的液体成规律性的往复周期振动；流道特性使得悬置产生高刚度，大阻尼；而大部分时间没有液体流动经过解耦盘，悬置表现出了明显的液压特征。在图7(b))中，解耦膜片在解耦盘间来回振荡(模型中解耦膜片与上、下解耦盘的间隙为1 mm)；振荡瞬间解耦膜片由于与解耦盘的撞击产生了非常大的瞬间加速度；这也是通过解耦盘液体的流量在很短的时刻流量有突变的原因。解耦液压悬置在大振幅激励下表现出了高刚度，大度阻尼的特性。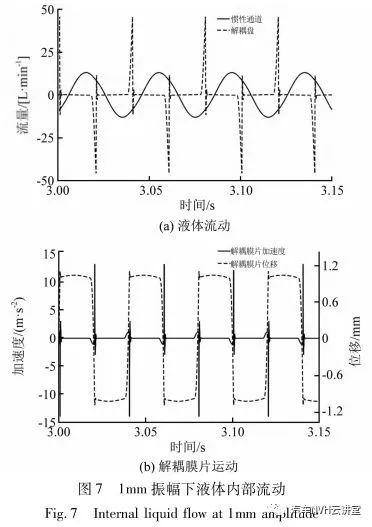
2 试验验证
利用MTS831测试解耦液压悬置的动态特性，试验装置见图8。
将悬置的上端通过螺栓与作动器固定连接；下端与试验台的固定工装连接。作动器给悬置上端输出恒定位移的扫频激励，并记录悬置产生的动态支反力。试验时，分别给悬置施加0.1 mm和1 mm振幅的1～50 Hz的扫频激励，频率间隔为1 Hz。试验结果与仿真结果的对比见图9和图10。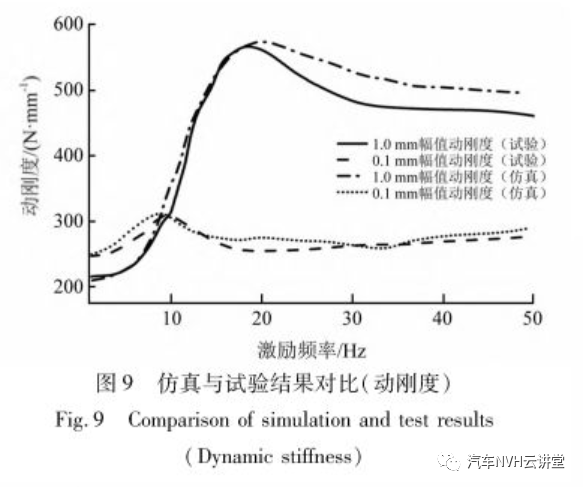
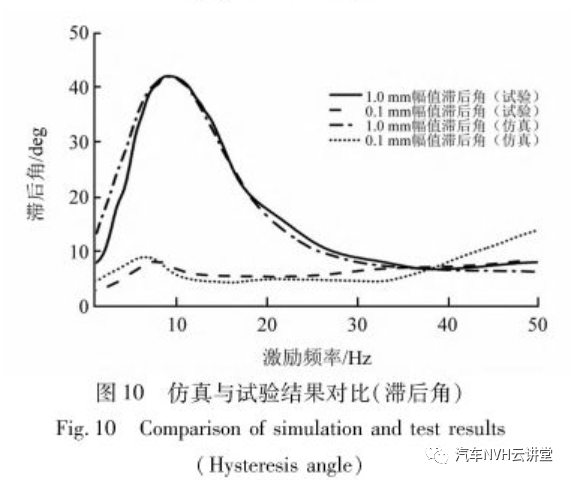
从图10可知：仿真结果与试验结果一致性较好。大振幅条件下(1 mm)：动刚度和滞后角出现的频率位置，峰值的幅值均有很好的一致性。小振幅条件下(0.1 mm)：试验结果也表现出了惯性通道内液体未起振的特性，悬置呈现的是橡胶主簧刚度特性。实验表明：文中建立的模型可以准确的表征解耦液压悬置的幅变，频变特性；并且能够准确描述不同工况下液体在液室内部的流动情况。3 包含液压悬置的整车模型建立
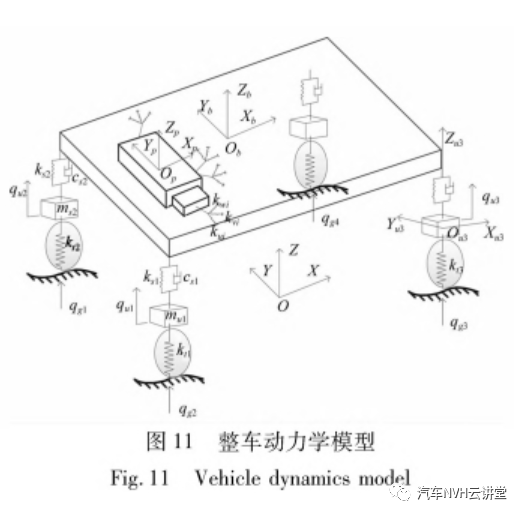
车辆行驶时，悬置要能够在效衰减发动机振动同时，较好的控制动力总成在受到大冲击时的振动。如图11所示，为了研究解耦液压悬置对这两类振动的控制情况，文中建立了包含动力总成、车身、悬架、轮胎在内的整车13自由度动力学模型，模型中动力总成横置，前轮驱动。模型中考虑了包含悬置系统在内的动力总成6个自由度(三个平动、三个转动)、车身的3个自由度(垂向、俯仰和侧倾)及4个非簧载质量的垂向自由度。静平衡状态时，参考整车坐标系O-XYZ，建立动力总成坐标系Op-XpYpZp和车身质心处坐标系Ob-XbYbZb。对于该整车模型位移有：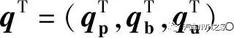 
其中qp为动力总成质心的位移， 
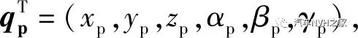其中xp，yp，zp分别为动力总成质心沿X，Y，Z轴的平动位移，αp，βp，γp为动力总成质心绕X，Y，Z轴的转动位移。qb为车身质心的位移， 
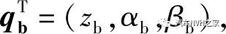且zb、αb、βb分别为车身质心在垂向，侧倾和俯仰方向的位移。qu为汽车四个非簧载质量在垂直方向的位移， 
根据牛顿第二定律，动力总成的振动方程为
式中：ki=diag(kiu,kiv,kiw)；ci=diag(ciu,civ,ciw)，分别为第i个悬置在其局部坐标系omi-umivmiwmi下的刚度矩阵和阻尼矩阵。Api为从Op-XpYpZp到omi-umivmiwmi的方向余弦矩阵。kpi和cpi分别为第i个悬置在Op-XpYpZp下的刚度矩阵和阻尼矩阵。rpi和rbi分别为第i个悬置在坐标系Op-XpYpZp和Ob-XbYbZb的位置。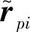 
和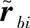 
分别为rpi和rbi的反对称矩阵。Mp为动力总成在坐标系Op-XpYpZp下的质量矩阵。以车身为研究对象，利用牛顿第二定律推导出车身的振动方程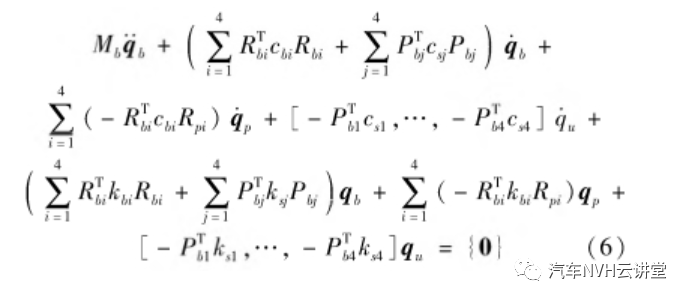
式中：Rbi=[1,ybi,-xbi]；Rpi=[0,0,1,ypi,-xpi,0]；Pbj=[1,ybj,-xbj]；ksj为第j个悬架垂直方向的刚度；csj为第j个悬架垂直方向的阻尼；kbi为第i个悬置在Zb方向上的刚度。Mb为车身在其坐标系Ob-XbYbZb下的质量矩阵。四个非簧载质量的振动方程可简化为4个独立的二自由度振动模型，振动方程在此不再赘述；利用上述振动方程可以得到整车13自由度振动方程。假设驾驶员在不踩油门的情况下，在0.1 s内匀速通过高50 mm的减速带；在模型中，给路面施加一个时常为0.1 s，幅值为50 mm的三角波激励；计算包含解耦液压悬置的整车动力学模型在车辆低速行驶过程中过减速带时的响应，计算分析与试验结果见第四节。4 整车试验验证及优化
4.1 整车试验验证
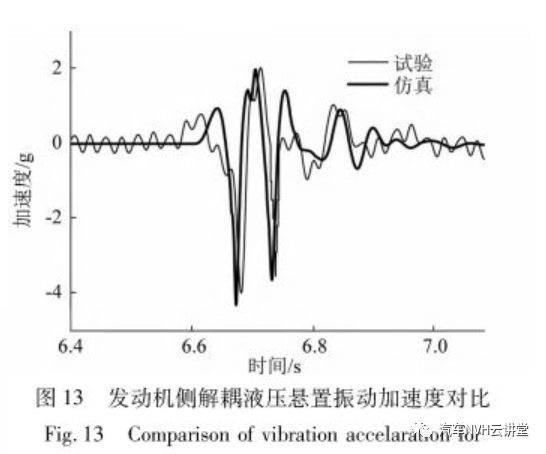
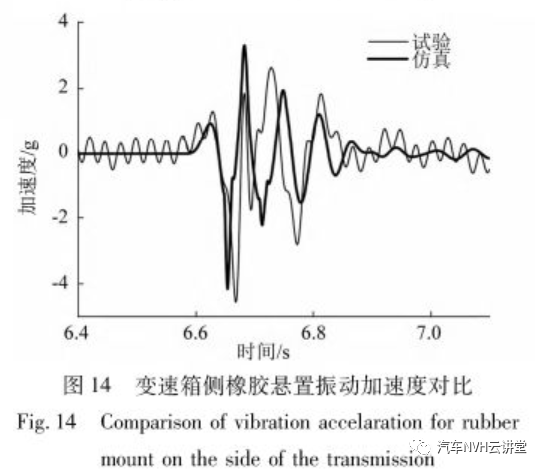
为了验证本文所建模型的有效性，进行了整车试验。试验车辆发动机侧悬置安装了解耦液压悬置，变速箱侧安装了橡胶悬置。试验时，在液压悬置的发动机侧和变速箱悬置侧分别布置加速度传感器，如图12所示。采集液压悬置在过减速带时的振动加速度，并与仿真结果对比，对比结果见图13～图14。为了排除高频振动的影响，试验测试结果对高于50 Hz的采集数据进行了低通滤波处理。
从图13、图14可知：由于安装了解耦液压悬置，在车辆过减速带时发动机侧振动加速度正向峰值明显小于变速箱侧，并且振动衰减迅速，有效的抑制了动力总成的晃动。仿真计算出的发动机侧悬置和变速箱侧悬置振动加速度峰峰值与试验结果分别仅相差4.5%和12%。仿真得到的系统动力学响应与试验结果一致性较好，验证了模型的有效性。4.2 优化方案
解耦液压悬置通过自身大阻尼特性能够有效衰减汽车过减速带时动力总成的振动。本文所建立的模型可以直接分析解耦液压悬置的结构参数对动力总成振动控制的影响。由于液压悬置结构参数较多，想要得到最优的设计方案，需要建立相应的优化函数进行计算。引入发动机侧悬置Z向振动加速度标准差(STD)作为优化目标进行分析。加速度标准差计算公式为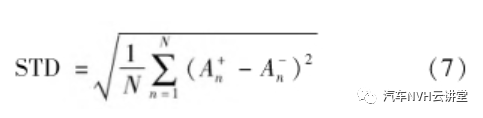
式中：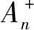 
为第n个振动周期里发动机Z向加速度的峰值； 
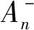为第n个振动周期里发动机Z向加速度的谷值。由上式可知，STD值越小，动力总成振动被控制的越好。本文中N=3。影响悬置液压特性的结构设计参数主要有：上液室体积刚度k；流道长度l；流道口面积A；解耦膜间隙d。以这4个参数作为设计变量考虑到实际零件布置空间，上液室体积刚度；流道长度；流道口面积变化范围不能超过±20%，同时为了保证小振幅条件下液压模块不共振，解耦膜间隙不能小于0.3 mm，即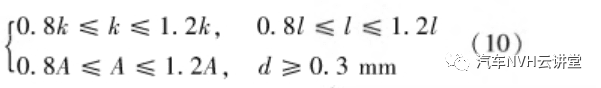
4.3 优化结果
本文采用序列二次规划法对所建立的优化模型进行优化，优化前后解耦液压悬置参数见表2，优化前后动力总成发动机侧悬置振动角速度对比见图15。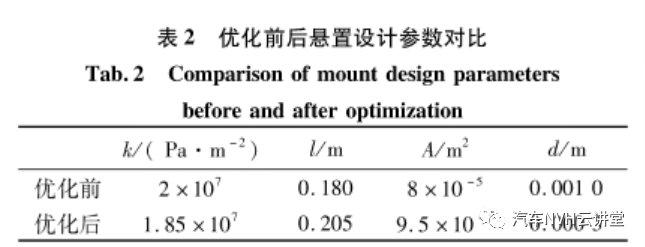
从图15可知，优化后由于阻尼特性的优化，解耦液压悬置处振动加速度峰峰值衰减到初始状态的40%，振动迅速衰减，优化效果良好。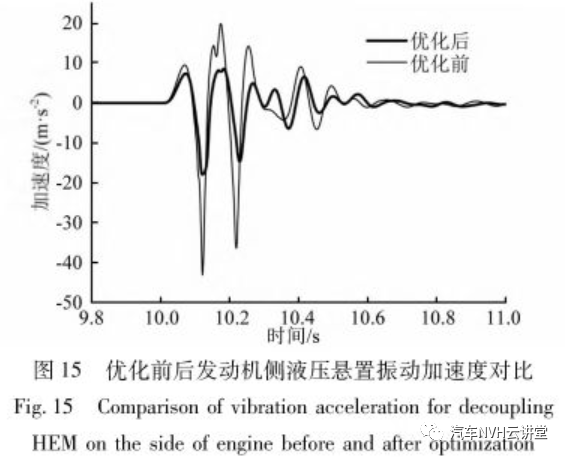
5 结 论
(1)考虑了橡胶材料内部摩擦，黏弹性特性；用连接管道的液压缸等效悬置的上、下液室及惯性通道；用质量块与非线性弹簧并联的方法等效解耦膜片在解耦盘间的运动，建立了解耦液压悬置分析模型。(2)计算分析出不同振幅，频率下的解耦液压悬置动态特性；研究了解耦液压悬置内油液的流动情况。结果表明：发现悬置的动刚度和滞后角的峰值随激励幅值的增加先增大后减小。在小振幅条件下，液体主要从解耦盘流动，液体在惯性通道内的阻尼特性可以忽略。在大振幅条件下，解耦膜片与解耦盘贴紧，液体主要从惯性通道流通，液体阻尼特性明显。最后，通过试验验证了所建模型的有效性。(3)建立了包含解耦液压悬置的整车13自由度模型，计算分析了车辆过减速带时的系统响应，仿真计算出的发动机侧悬置和变速箱侧悬置振动加速度峰峰值与试验结果分别仅相差4.5%和12%，实车试验验证了分析结果的准确性。最后，以抑制车辆过减速带衰减动力总成振动为目标给出了液压悬置的优化方案，优化后的解耦液压悬置处振动加速度峰峰值衰减到初始状态的40%，为解耦液压悬置的正向设计与匹配提供理论支撑。作者：刘雪莱1，杜 浩1，陈俊杰2
1.上海汽车集团股份有限公司技术中心
2.江西理工大学 机电工程学院
著作权归作者所有，欢迎分享，未经许可，不得转载
首次发布时间：2023-12-01
最近编辑：4月前
