结构动力学仿真分析的振动理论基础知识,以及什么是解耦?
本号课程《结构动力学完整解决方案》经过近一个月的直播培训,11月28日顺利完成。计划直播13次,实际直播14次,课程总时长约30小时。感恩学员们的大力支持。后续群内保持互动,持续学习,共同进步。
自始至终,我们的课程主要是针对工程师角色,定位为应用层面。所以在理论上没有过多展开,更多的时间放在了工程实践方面。
但理论知识不可能完全避开。我们把理论知识分为基础知识和求解计算。基础知识包含基本概念、基本原理、基本方程等;求解计算是指方程的求解计算过程和方法。
因为仿真软件采用数值解法来求解方程,所以理论知识中的求解计算部分,绝大多数可以避开,但必须加强对基础知识的理解和掌握。
理解和掌握结构动力学的基本方程和基本概念,非常有助于判断动力学问题,能显著提高仿真分析能力。
本文的叙事逻辑和一般教材不同。本文先从多自由度无阻尼系统入手,因为绝大多数的结构模态仿真都属于此类。然后引入阻尼项,导致特征值与特征向量解由实数变为共轭复数。再引入比例阻尼的概念,将多自由度阻尼系统解耦为多个单自由度阻尼系统。最后再介绍单自由度阻尼系统的解法。
一般教材的叙事逻辑是从单自由度到多自由度,从无阻尼到有阻尼。
动力学方程,也称为运动方程,控制方程等。

已知M和K,根据下式可以求得固有圆频率(特征值)ω,ω为n个实数。

并且按照从小到大排列:
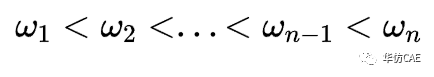
根据下式可以求得固有振型(特征向量)Φ,Φ为n个实数向量。
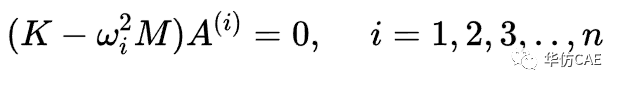

至此知道,固有圆频率和固有振型的来源。
各阶振型组成的振型矩阵:

根据下式可以求得主质量矩阵Mp和主刚度矩阵Kp:


至此知道,主质量矩阵和主刚度矩阵的来源。

已知M、K、C,根据下式可以求得特征值λ,因为阻尼的引入,λ变为n对共轭复数。

根据下式可以求得特征向量Φ,Φ为n对共轭复数向量。

至此知道,引入阻尼,特征值和特征向量都变为共轭复数。
利用无阻尼下的特征向量Φ
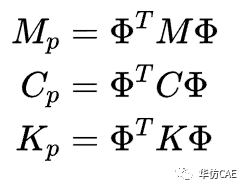
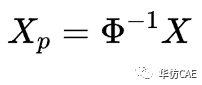
比例阻尼,也叫做瑞利阻尼。假设C为比例阻尼,则Cp为对角矩阵。


当Mp、Cp、Kp都为对角矩阵。

就是n个单自由度阻尼系统的动力学方程组
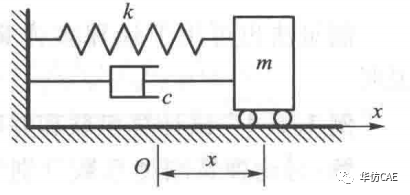
振动力学模型。
动力学方程。
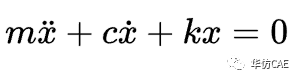
求解过程,特征值为共轭复数,


(截图自刘延柱陈立群《振动力学-第3版》)
解耦,全称为解开耦合,将耦合关系变为不耦合关系。
耦合关系是指两个自由度之间有能量交换,不耦合关系则指两个自由度之间没有能量交换。
对于比例阻尼,可以将多自由度阻尼系统解耦为单自由度阻尼系统,但需要将多自由度阻尼系统的实际自由度(物理的)先转换为主自由度(数学的)。
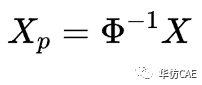
解耦之后,求解得到主自由度Xp,需要再进行一次转换,才能得到实际自由度X。
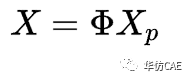
来源:华仿CAE