基于有限元计算程序的探究(上)—网格划分、刚度矩阵求解、载荷施加
前言
在我们从学校踏入职场,从事有限元计算的初期,绝大多数人都是一拿到模型就导入商业软件中,一顿操作,洋洋洒洒从几何处理、网格划分、加载计算,最后看到五颜六色的云图,颔首微笑,自信满满,以为完全掌握了有限元计算这项技能,打算在该领域大显身手、扬名立万。随着从业时间的增长,开始的几年里进步神速,真正实现了“从入门到精通”,但是在以后几年中,还是在“原地踏步”,成长性不够。这可能就是太依赖于商业软件导致的,商业软件是一把双刃剑,给予我们方便的同时,也扼杀了我们探求其内在算法的欲望,没有理论上升的空间。在疲于应付项目的过程中,不经意间可能已经忘记了有限元计算的理论基础:什么是形函数?如何用节点位移来表示单元内任意一点的位移?单元刚度矩阵如何“组装”成整体刚度矩阵?等等。因此在闲暇时刻,有必要翻一翻理论教材,细细品味一下其中的奥秘,对我们真正理解“有限元”是有帮助的。这里推荐周博老师的《有限元法与MATLAB》著作,它是一本非常好的书,在讲解基础知识的同时,也用Matlab程序实现了各知识点的贯穿,帮助我们更好的理解一些“生涩”的词汇。
1. 网格划分
有限元计算的第一步,就是划分网格,其函数为:
[Nxy, Enod]=mesh2d3n(x12,y12,m,n)
源程序:
function[Nxy,Enod] = mesh2d3n(x12,y12, m, n)
x =linspace(x12(1),x12(2),m);
y =linspace(y12(1),y12(2),n);
[X,Y] =meshgrid(x,y);
Enod =delaunay(X,Y); %%%生成3结点单元结点信息矩阵
h1 =triplot(Enod,X,Y); %%%绘制三角形单元的离散网格
set(h1,'color','k')
axisequal
[en,ny]= size(Enod); %%%en为单元数,ny为每个单元节点数3
for i =1:en
x_sum = 0;
y_sum = 0;
xy_sum = 0;
for j = 1:ny
ID = Enod(i,j);
x_sum = x_sum + X(ID);
end
xc = x_sum/ny; %%%计算三角形单元形心横坐标
yc = y_sum/ny; %%%计算三角形单元形心纵坐标
h2 = text(xc,yc,num2str(i)); %%%在三角形形心处标注单元编号
set(h2,'color','b')
set(h2,'fontsize',10)
end
for k =1:m*n
Nxy(k,1:3) = [k, X(k), Y(k)];
h3 = text(X(k), Y(k),num2str(k)); %%%在节点坐标处标注节点编号
set(h3,'color','r')
set(h3,'fontsize',10)
end
Enod =[(1:en)', Enod]; %%%把单元编号放在第1列,2-4列为节点编号
end
clear;clc
x12=[0,3];
y12=[0,3];
[Nxy,Enod] = mesh2d3n(x12,y12, m, n);
Axis([-0.5,3.5,-0.5,3.5]);

图1 网格划分结果
A =0.5*det(A); %%%三角形单元面积
求得单元应变矩阵后,再求单元刚度矩阵,其函数为:
KE=EstiffM2d3n(xy,mat)
参数意义:
xy:3行2列矩阵, 1-2列分别是单元节点的横、纵坐标;
mat:1行3列矩阵,1-3列分别是材料弹性模量、泊松比、单元厚度;
KE:6行6列单元刚度矩阵
源程序:
function KE = EstiffM2d3n(xy, mat)
函数应用实例
运行程序后,可以得到这两个单元的刚度矩阵,见图2。

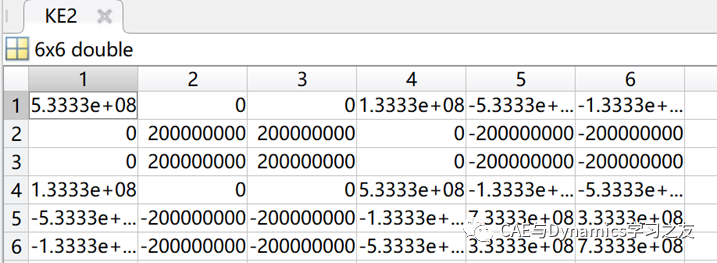
图2 计算得到的单元刚度矩阵
3. 整体刚度矩阵
KS=SstiffM2d3n(Nxy,Enod,Emat)
参数意义:
Nxy: N(节点总数)行3列矩阵, 1-3列分别为节点编号、节点横、纵坐标;
Enod:M(单元总数)行4列矩阵,1-4列分别为单元编号、单元所含3个节点编号。
Emat:M(单元总数)行4列矩阵,1-4列分别为单元编号、弹性模量、泊松比、单元厚度
源程序:
functionKS = SstiffM2d3n(Nxy, Enod, Emat)
M =size(Enod, 1);%%%单元总数量
KS =zeros(2*N, 2*N); %%% 整体刚度矩阵初始化
for j =1:M
ii = Enod(j, 2); %%% 依次提取各单元的节点编号
jj = Enod(j, 3);
mm = Enod(j, 4);
sn = [ii, jj, mm]; %%% 节点编号矩阵
xy = Nxy(sn,2:3); %%% 提取节点坐标
mat = Emat(j, 2:4); %%% 提取材料属性
KE = EstiffM2d3n(xy, mat); %%% 调用EstiffM2d3n生成单元刚度矩阵
sn = [2*ii-1, 2*ii, 2*jj-1, 2*jj, 2*mm-1,2*mm]; %%% 对号入座数组
KS(sn, sn) = KS(sn, sn) + KE; %%%将单元刚度矩阵累加到整体刚度矩阵
end
end
函数应用实例
clear;clc;
x12= [0,2];
y12= [0,1.5];
[Nxy,Enod]= mesh2d3n(x12,y12, 3, 3); %%%结构的三角形网络离散
axis([-0.2,2.2,-0.2,1.7])
[M,N] = size(Enod); %%%M为单元个数
Emat(1,1:4)= [1, 180e9, 0.35, 5e-2]; %%%材料属性
fori = 2:M
Emat(i, 1:4) = Emat(1,1:4); %%%对每一个单元赋材料属性
end
KS =SstiffM2d3n(Nxy, Enod, Emat) %%%生成整体刚度矩阵
运行后,整体刚度矩阵如图3。

图3 整体刚度矩阵
4. 载荷的施加
需要根据载荷施加情况,需要计算等效节点载荷,其函数为:
SP=SloadA2d3n(EP,N)
EP:4列矩阵,1-4列分别为单元编号、节点编号、载荷方向、载荷大小;
N:节点总数
SP:2N行1列节点载荷矩阵
源程序:
functionSP = SloadA2d3n(EP,N)
[n,m]=size(EP);%%% 提取载荷数量n
SP(1:2*N,1)= 0;%%% 载荷矩阵初始化
fori=1:n
sn = 2*EP(i,2)+EP(i,3)-2; %%%施加载荷的位置与方向
SP(sn) = SP(sn) + EP(i,4); %%%施加载荷的大小
End
函数应用实例
clear;clc;
N= 9;
EP= [7, 8, 1, 3.5e3;
7, 6, 2, -(2+2/3)*1e3;
7, 9, 2, -(2+4/3)*1e3;
5, 3, 2, -2/3*1e3;
5, 6, 2, -4/3*1e3];%%%受载荷信息:1-4列分别为单元编号、节点编号、载荷方向、 载荷大小;
SP= SloadA2d3n(EP,N);%%%载荷列阵
运行后,得到载荷列阵,结果如图4。
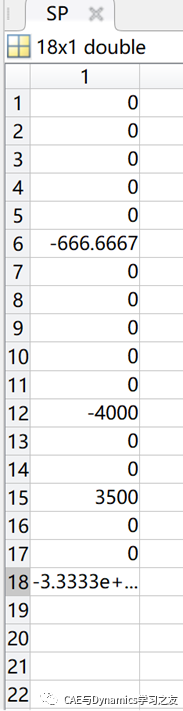
图4 载荷列阵




