傅里叶分析(1)
本文介绍了傅里叶分析及其在CFD的应用。由于篇幅原因,将其拆分为系列化文章:
连续信号的傅里叶分析 离散信号的傅里叶分析 傅里叶分析在CFD的一些应用 在Fluent进行傅里叶分析的操作
傅里叶分析是信号分析中常用方法之一。傅里叶分析可将信号在时域和频域之间进行转换,从而分析信号在频域上的相关问题,如光的颜色、结构共振点、乐器声品质等。
傅里叶分析(Fourier analysis)根据信号的时域数据特征,分为 4 个类别:
傅里叶级数(Fourier series,FS):周期连续信号 傅里叶变换(Fourier transform,FT):非周期连续信号 离散傅里叶变换(discrete Fourier transform,DFT):周期离散信号 离散时间傅里叶变换(discrete-time Fourier transform,DTFT):非周期离散信号
傅里叶级数描述了将周期函数(其周期为 T)转换为若干个三角函数之和的方法。被转换的周期函数在单个周期内允许存在有限个间断点(如方波函数)。
傅里叶级数的最基本表示方法为若干正弦、余弦函数的和,即正弦-余弦形式:

其中,各项系数的取值为:
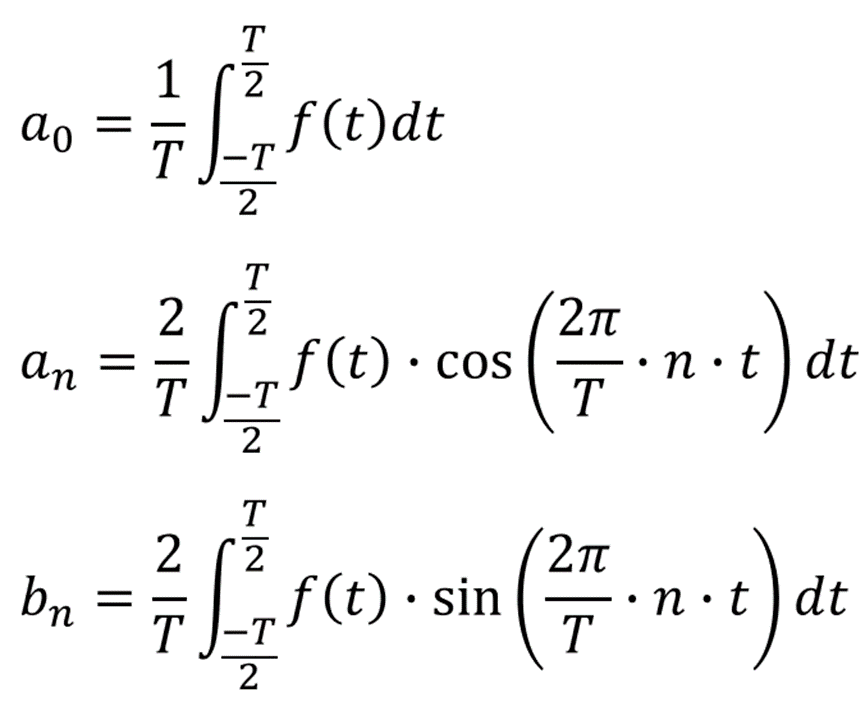
通过三角函数变换,傅里叶级数也可表示为幅值-相位形式:


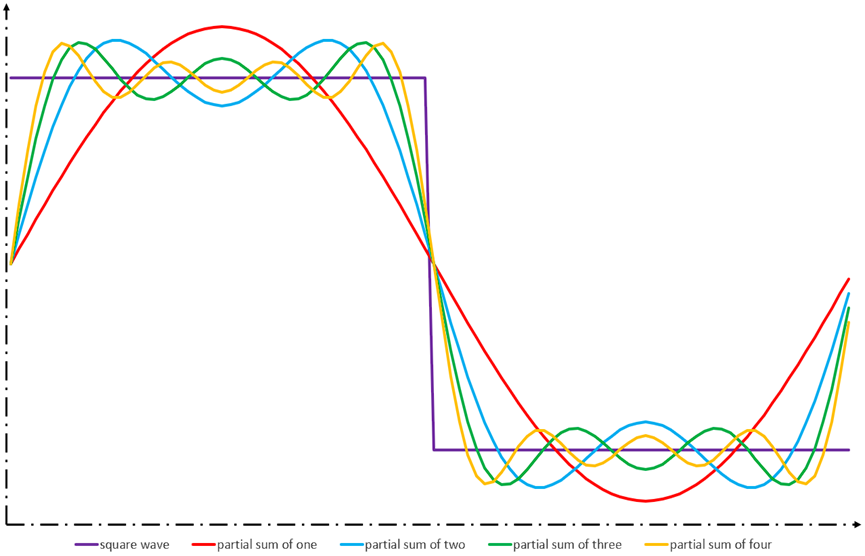
将周期函数转换为傅里叶级数的方法也称为谐波分析(harmonic analysis),每个级数项根据 n 取值称为 n 次谐波(harmonics)。理论上,周期函数包含无穷多谐波,实际应用中通常只取前若干次谐波截断近似。截断的谐波次数越高,则越接近原始函数。
如图为方波的谐波叠加结果对比,很显然,使用的谐波数量越多则越接近方波真实形状。
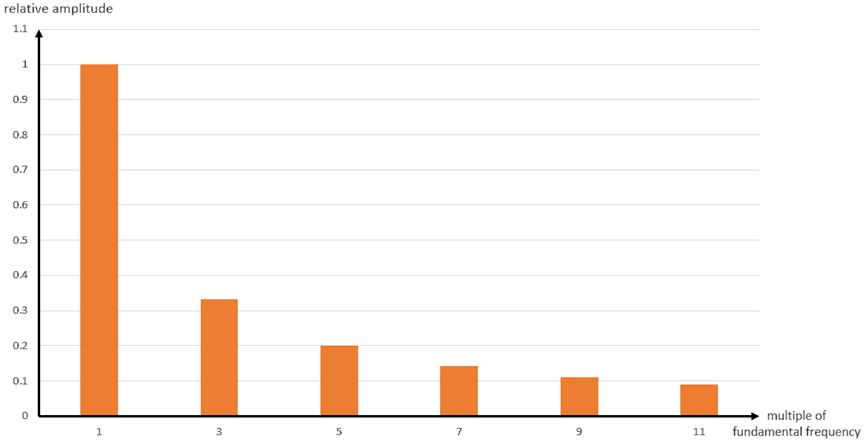
周期函数的频谱特征为:
一次谐波频率(基频)为 1/T n 次谐波频率为 n/T,为基频的整数倍 可能存在 0 幅值的谐波 幅值非 0 的谐波,次数越高,幅值越小
偶数次谐波(二次谐波、四次谐波等)幅值为 0 奇数次谐波(一次谐波、三次谐波等)幅值为基频幅值的 1/n
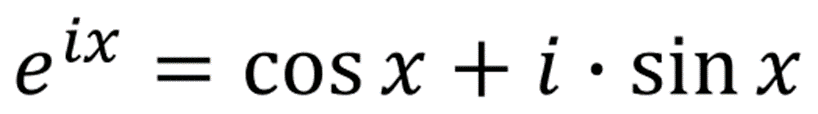
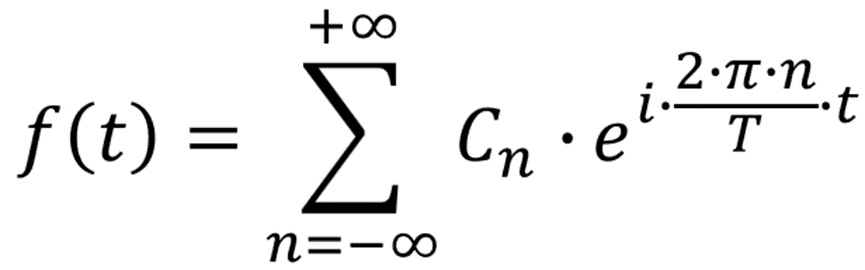
指数形式系数取值为:
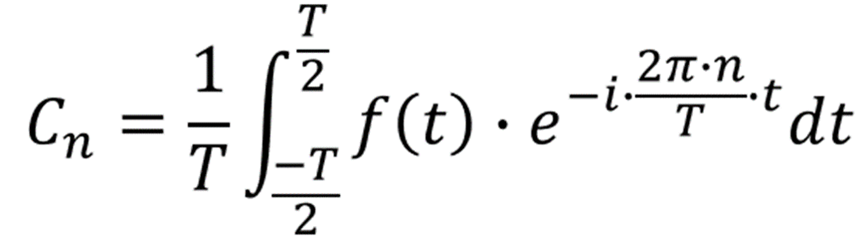
指数形式和正弦-余弦形式的系数关系为:

傅里叶变换为傅里叶级数针对非周期函数的扩展。
非周期函数为周期趋近于无穷大的极限状态,此时基频 1/T 趋近于 0,频谱从离散点 n/T 变成连续函数。在数学处理中,傅里叶级数的求和操作变成傅里叶变换的求积分操作。
傅里叶变换为时域到频域的变换,其变换结果为频域函数。傅里叶变换类似于傅里叶级数中,求级数的各项系数。
傅里叶变换计算公式为:

傅里叶逆变换为频域到时域的变换,其变换结果为时域函数。傅里叶逆变换类似于傅里叶级数中,根据级数各项表达式求原函数。傅里叶逆变换计算公式为:
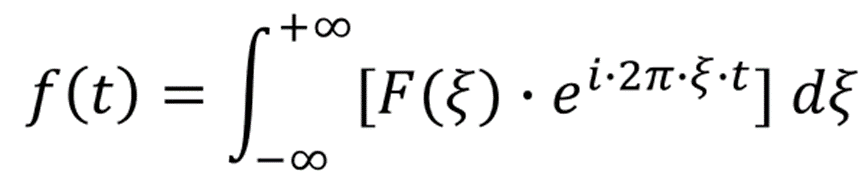
比较指数形式傅里叶级数和傅里叶变换公式,在 T 趋向于无穷大时:
频谱的频率取值从离散点 n/T 变成连续变量 ξ 傅里叶级数的系数从离散数值 Cn 变成连续函数 F(ξ)

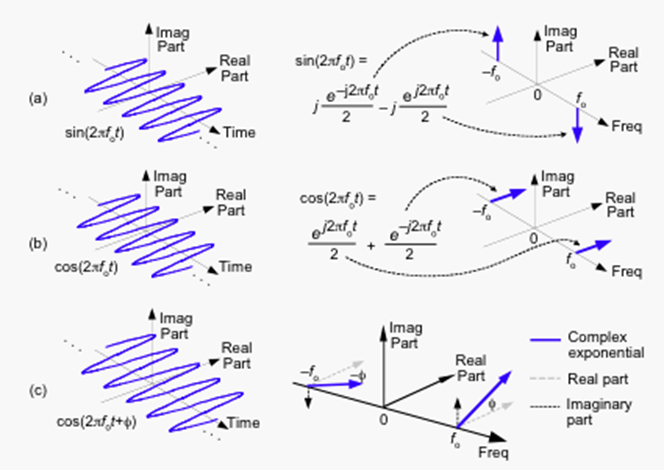
物理意义的频率定义为单位时间内的重复次数,其取值必然为正数,不存在负频率的情况。
对于多个互相关联的信号,可将其进行组合以方便分析和处理,典型应用场景如波干涉分析等需要考虑信号相位影响的问题。一种常用方法为将信号表示为 z=f(t)+i*g(t) 的复函数形式。
复信号有实部和虚部两个自变量,为三维空间的函数。在三维空间中,定义旋转方向需要满足右手螺旋法则,负的角速度旋转方向与右手螺旋法则相反。根据角速度与频率之间的数量关系,可得到负频率。物理意义上的频率定义,其实际为负频率的绝对值。
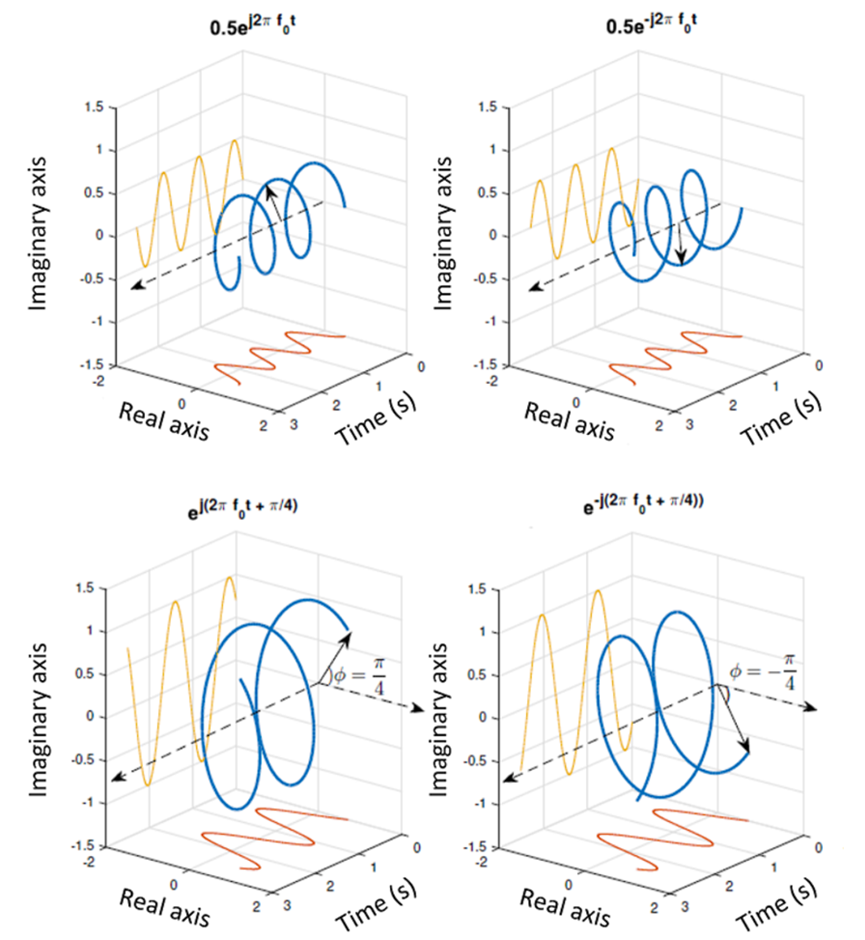
频域函数 F(ξ) 为复函数,即存在复频率。复频率表示了频率的相位。
若 f(t) 是纯实数的函数,其傅里叶变换后的频域函数 F(ξ) 为偶函数,其幅值和相位特点为:
幅值为频率的偶函数 相位为频率的奇函数
信号在不同频率的强度差异可能跨数个数量级,难以直接比较或分析差异。工程应用中,也需要考虑信号之间的强度比例问题(如传感器信噪比),而不仅是信号强度本身。
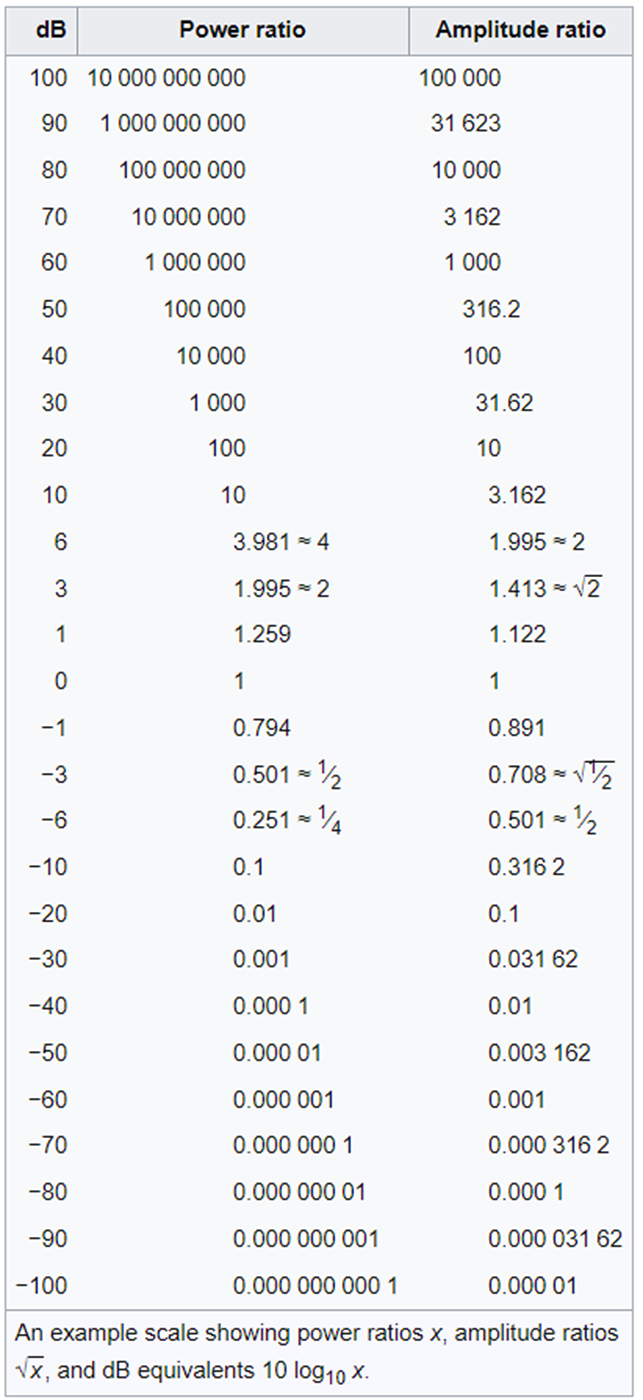
为此,引入单位贝尔(B)来表征信号强度之间数量级关系。实际工程中通常采用分贝(dB),其换算为 1 dB = 0.1 B。
若比较标准为功率或与之成相关的物理量(如光强度、声强度等),dB 的数值计算公式为:
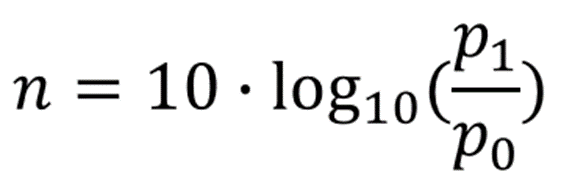
若比较标准为与功率的平方根成比例的物理量(如速度、电流、电压等),dB 的数值计算公式为:
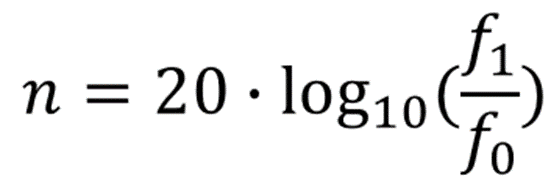
上述算式中,p1 和 f1 为实际信号的物理量,p0和 f0 为参考基准值。由于 dB 定义基于对数比例,因而不满足线性叠加关系。