基于蒙特卡罗的LSOPT和LSDYNA碰撞分析
以下文章来源于CAE数值优化轻量化 ,作者方永利
本文摘要(由AI生成):
本文介绍了在设计过程中应用鲁棒性和可靠性概念的重要性,特别是当考虑输入变量的可变性时。通过使用蒙特卡罗模拟,可以预测由于随机变量导致的不同结果概率。文章以碰撞件为例,详细描述了如何使用CAE软件进行蒙特卡罗分析,包括创建分析任务、定义参数、时间历程结果和设计响应等步骤。最后,通过设定样本点和优化方法,提交求解并得出结果。
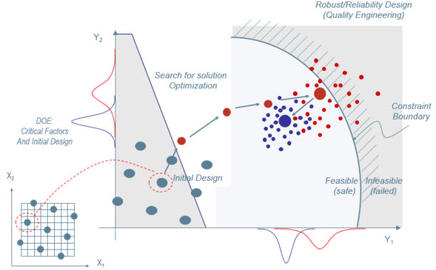
模拟通常以确定性的方式运行。对于给定的输入变量集,相应的输出总是相同的。但在现实世界中,由于输入变量的可变性,如制造公差、几何特性等,输出通常不是一个固定值,而是在平均值附近分布。由于这种行为,在确定性模拟中有效的设计可能会导致实际生产中的缺陷产品。为了在设计阶段避免这一问题,我们必须考虑设计变量的可变性,应用鲁棒性和可靠性的概念和方法来保证设计的鲁棒性和可靠性。
蒙特卡罗模拟用于模拟由于随机变量的干预而难以预测的过程中不同结果的概率。它是一种用来理解风险和不确定性在预测和预测模型中的影响的技术。



1.打开工作目录
2.创建文件名
3.问题描述
4.作者信息
5.样本点方法描述
6.模块名称

创建完成后如上界面。

打开Task Selection,选择Monte Carlo analysis

定义LSDYNA Stage模块:
1.选择模块为LSDYNA
2.选择求解器路径,这里可以选择任意适用的版本求解器(可以使用官网任何版本的求解器,包括任何SMP和MPP版本,有需要的可以私信我获得方法)
3.选择K文件
4.设置LSDYNA模块的CPU分配

定义参数:
1.通过读入上步的K文件,可以直接识别两个参数:材料屈服强度和���度。

定义时间历程结果:
1.选择Histories
2.选择NODOUT
3.设置时间历程名称
4.选择结果类型
5.选择成分
6.选择节点ID

定义设计响应:

定义参数:
1.双击Setup
2.选择变量类型为Noise
3.选择变量分布类型,正态分布
4.新增一个变量分布类型



设置样本点:
1.选择Latin Hypercube
2.设置样本点个数100

设置优化方法:
计算结果: