Pointwise&Fluent复杂气动问题拼接重叠网格技术详解
- 作者优秀
- 优秀教师/意见领袖/博士学历/特邀专家/独家讲师
- 平台推荐
- 内容稀缺

导读:在求解复杂外形流场时,网格技术是影响计算结果和效率的关键。网格由单块网格发展到了多块网格,多块网格存在网格量大生成难度大,严重影响了计算效率。正对此情况,发展了拼接网格技术和重叠网格技术。拼接网格,块与块之间通过面连接,不要求网格线连续对接,网格块之间相互独立,拓扑结构自由灵活,这样便可以有效地减小网格生成难度。重叠网格的每个部件网格是独立生成的,只要模型存在缝隙,各部件相互独立皆可使用重叠网格技术。
本文选取四个模型,由简到繁,纯机翼、机翼+偏襟翼、机翼+偏襟翼+射流、机翼+偏襟翼+射流+螺旋桨旋转模型展示结构重叠网格/非结构重叠/非结构拼接的计算全流程讲解。
1、重叠网格
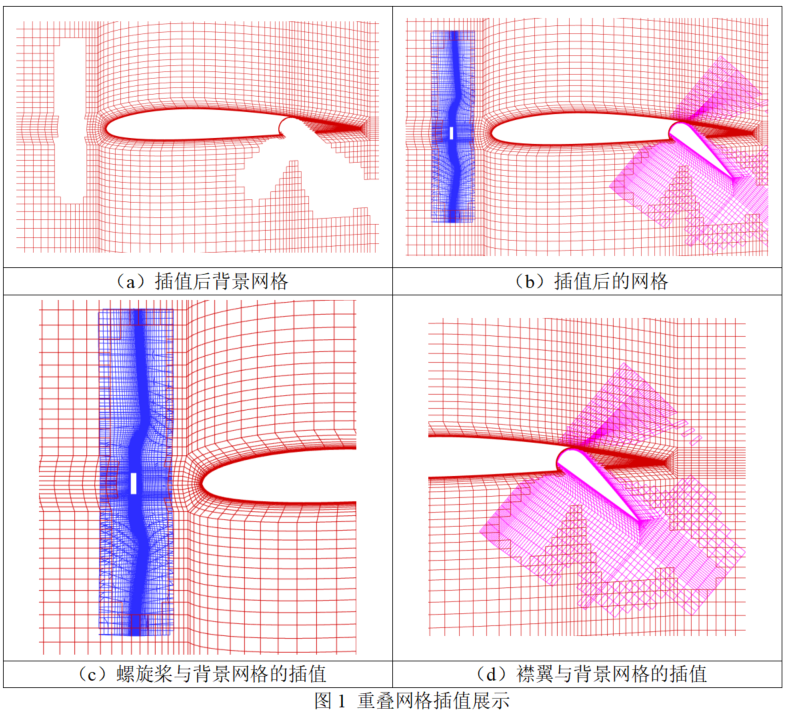
重叠网格法可分为重叠结构网格法、重叠非结构网格法。重叠网格法最初是由结构网格发展而来,结构网格因其拓扑关系明确、离散流场空间所需网格量和存储空间小、计算效率高等优点在数值计算中使用广泛,但对于复杂几何外形的问题,重叠结构网格方法的网格分块较多,增加了网格生成的难度和计算时间,因此在工程应用中的发展受到限制。非结构网格本身具有较强的自适应调整能力、生成方法简单、能够适应复杂几何外形,重叠非结构网格方法的最大优点是在生成复杂外形的流场网格时所用网格分块更少,但相比于重叠结构网格,重叠非结构网格在相同网格数量条件下,占用存储大、计算耗时、耗散较大。不论是结构还是非结构网格它们的理论基础和主要思想是一致的,都需要挖洞和建立嵌入网格关系,且在数值迭代过程中都需要在重叠区域边界上进行网格的插值运算。Fluent中重叠区域通过overset边界面的设置来使插值运算得以实现。
重叠网格常用于部件运动(襟翼、副翼、控制舵、螺旋桨旋转、风扇转动)、分离投放、多体运动等场景中。各部件网格独立制作,在插值面上保持网格密度相当,来实现高精度的插值运算。
2、拼接网格
拼接网格(Cross Grid)又称面搭接网格(patched Grid),其特点是在网格块与块之间通过公共面进行连接,网格线不需要严格对接,即网格之间的拓扑关系被交界面切开,因此,网格块之间的拓扑关系相互独立,并通过相互相交的交界面进行信息传递。其优点是:能使复杂外形网格相对简单,网格量较小;采用通量守恒的交界面传值,保证一定的工程精度。网格前置处理,即确定交界面两侧边界单元的插值关系,在交界面两侧为各网格的拼接面。在Fluent中通过设置成对的interface面来实现插值。
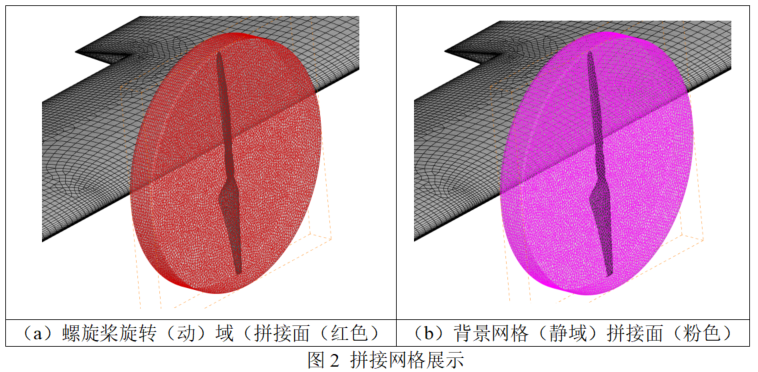
拼接网格与重叠网格在本质上相同,均为对复杂外形的网格生成进行简化处理。两者均能很好地对复杂外形进行简化,降低了网格生成的难度,并减小了网格量,但拼接网格和重叠网格各有优缺点,需结合实际情况进行适当的选择。在网格生成上,重叠网格具有较强的灵活性,而拼接网格在网格生成上更为复杂,工作量较重叠网格多。在插值精度上,拼接网格精度高于重叠网格。拼接网格在插值关系以及通量守恒性等方面优于重叠网格;尤其体现在含有网格运动的计算仿真中。在非定常运动的每一迭代时间步上,重叠网格不仅需要更新各子域的网格而且还要对子域的重叠区网格进行插值和更新,从而导致计算量增大。而对于采用公共面的拼接网格来说,边界点的选取以及插值关系的寻找很容易实现自动化。
流体力学仿真研究中经常面临一些旋转流动的问题,比如风扇、风力发电机叶片、泵、马达转子、螺旋桨等,这些研究当中均涉及到旋转流动常采用多重参考系模型(Multiple Reference Frame,MRF)和滑移网格模型(Sliding Meshes,SM)。 不管是MRF模型还是SM模型进行网格制作时,其本质上就是拼接网格的制作,区别在于MRF模型拼接面网格可以是共节点或者不共节点;单SM模型拼接面网格必须是不共节点。
1、MRF模型
2、滑移网格
滑移网格模型方法可以对瞬态非定常流动进行求解,与多重参考系模型一样,由动域和静域组成,区域之间通过Interface进行流场信息的交换。区别在于滑移网格模型中动域是真实运动的,区域之间允许相互转动。在滑移网格的求解过程中,至少包含两个相对运动计算域,每个计算域与相邻的计算域之间至少一个交界面进行流场信息的传递。交界面上的速度需与交界面垂直,故采用圆柱形作为流场动域。
MRF方法不会使相邻的两个运动区域间产生相对运动(可能是运动或静止);用于计算的网格依然是固定的。被分界面隔开的动域采用运动参考系方程进行求解,而静止的部分则采用静止参考系方程来求解。滑移网格模型对于多区域计算问题与多参考系模型相似,但是滑移网格模型中旋转域和静止域之间是可以转动的,所以旋转域的转动是真实存在的,更加符合实际。
1、计算条件
偏襟翼(起飞构型)、螺旋桨旋转模型起飞状态,高度0Km,来流速度0.2ma(约68m/s),攻角10°(矢量分解为0.173648032(+Y方向,厚度/高度方向),0.984807779(+X方向,流向)),湍流模型SST模型,理想气体,压力基,couple耦合算法。

2、网格模型
基于结构网格思路,制作机翼结构对接网格;偏襟翼、襟翼射流、偏襟翼+襟翼射流+螺旋桨旋转重叠网格。其中,偏襟翼、偏襟翼+襟翼射流、偏襟翼+襟翼射流+螺旋桨旋转也可采用拼接网格进行制作,本文相关课程中未进行结构拼接网格的制作及计算,只进行了结构重叠网格的研究。

基于非结构网格思路,制作了非结构的机翼、机翼+偏襟翼、机翼+偏襟翼+射流网格;制作了机翼+偏襟翼+射流+螺旋桨旋转拼接网格(包含共节点及不共节点网格)。制作了机翼+偏襟翼、机翼+偏襟翼+射流、机翼+偏襟翼+射流+螺旋桨重叠网格。

3、计算结果
结构系列网格计算了机翼、机翼+偏襟翼、机翼+偏襟翼+射流压比(1.2及3.0)共四条升力特性曲线。合理布置襟翼前缘射流缝的位置、高度、机翼与襟翼的合理搭配,可以很好的控制襟翼表面的流动反向,射流引射作用加强机翼表面流动,增加机翼环量进而增加升力系数。射流可以大幅提高升力系数,消除流动分离。

结构/非结构网格,重叠或拼接网格计算结果如表1所示。在单机翼模型中,结构、非结构网格计算获得的攻角10°的升力系数分别为,0.884和0.879,误差为5.66%。在偏襟翼无射流条件下,非结构、非结构重叠、结构重叠计算升力系数结果分别为1.132、1.077、1.14,非结构网格与结构重叠网格结果一致,与非结构重叠相差5.5%。在偏襟翼射流条件下,非结构、非结构重叠、结构重叠计算升力系数1.30、1.443、1.536,重叠网格计算结果均高于非结构网格,结构重叠结果高于非结构重叠网格。在螺旋桨旋转模型中,非结构重叠与结构重叠计算结果一致,均高于非结构拼接网格。拼接网格共节点、不共节点及滑移计算结果很一致(滑移网格计算代价大,未完全收敛),这也表明拼接面插值精度的可靠性;MRF算法的优点,计算结果可靠,计算代价低。

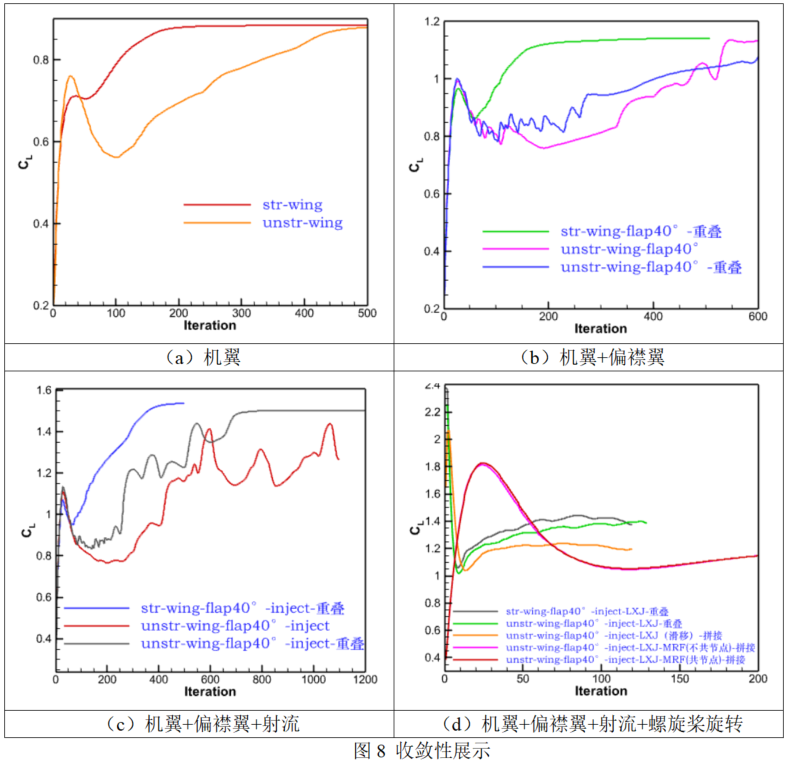
4、收敛性比较
图8展示了相同模型、不同计算网格之间的收敛性比较。在定场计算中,前三幅图结果表面,结构网格的收敛性优于非结构;结构网格收敛速度快、计算稳定。在复杂的射流计算条件下,襟翼射流的非结构重叠网格计算一致处于波动状态,收敛趋势差,射流对网格质量、射流区域的网格密度要求极高,需要特别注意。在MRF模型的计算中,拼接面共节点和不共节点收敛趋势相同,计算结果相同。在非定常计算中,每个迭代步的内迭代步为20步,一共计算迭代步约120步以上,未完全收敛,呈现周期性波动。
部分状态计算动画展示如下:
|
|
机翼+偏襟翼(结构重叠) | 机翼+偏襟翼+射流(结构重叠) |
|
|
机翼+偏襟翼(非结构重叠) | 机翼+偏襟翼+射流(非结构重叠) |
|
|
机翼+偏襟翼+射流+螺旋桨(结构重叠) | 机翼+偏襟翼+射流+螺旋桨(非结构重叠) |
|
|
机翼+偏襟翼+射流+螺旋桨MRF共节点(非结构拼接) | 机翼+偏襟翼+射流+螺旋桨MRF不共节点(非结构拼接) |
| |
| 机翼+偏襟翼+射流+螺旋桨(非结构拼接) |
6、部分流场展示
流场图显示,射流可以有效的消除襟翼表面的反流及空间涡,增加环量,进而提高升力系数;螺旋桨的转动会讲扰动传递到螺旋桨的后方区域,使流体加速流通。

7、网格收敛策略
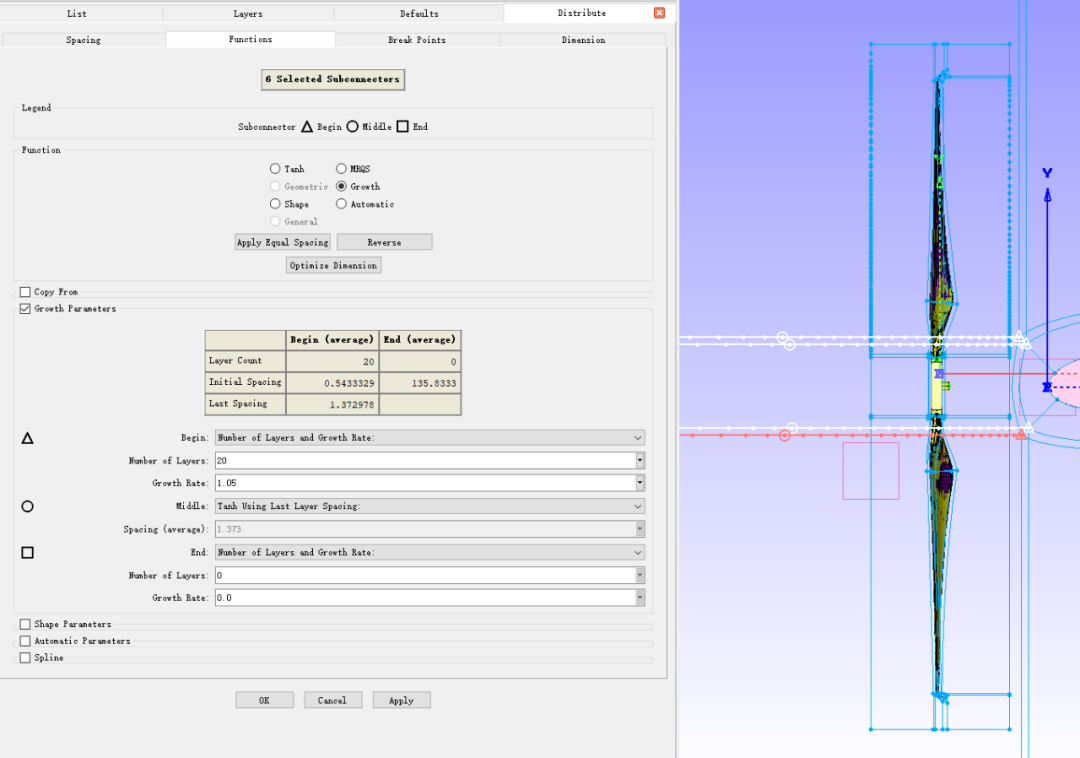
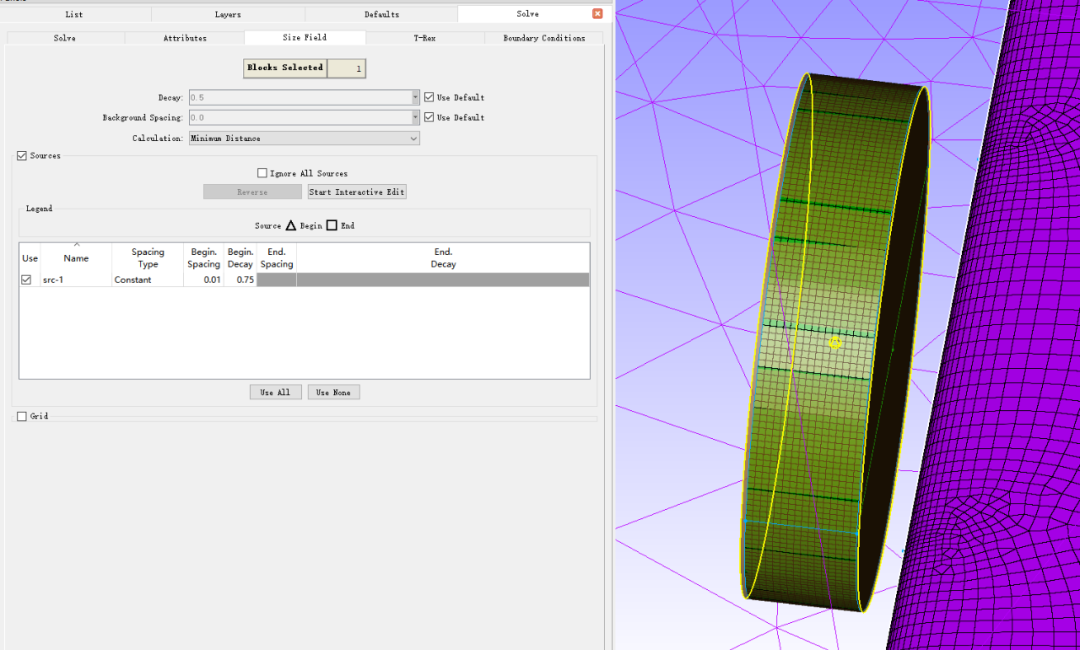
在非结构拼接网格制作时,如果不涉及动模型运动就可以使用共节点的方式,不存在额外的插值计算;涉及网格运动时,可以先生成其中一个域的拼接面网格,然后复 制该网格绕选择轴线旋转一个角度(一般一个很小的角度),这样在拼接面上的网格是具有相同的分布和网格量。

识别下方二维码,立即试看