ACP铺层设计的玻璃纤维增强复合材料电杆的挠度仿真分析及优化
相比于传统电杆,玻璃纤维复材电杆强度高、韧性好,受力不易折断, 但其偏大的挠度阻碍了其在一定场景下的大规模应用。对于纤维缠绕复材电杆来说, 玻璃纤维铺层方式和角度对其抗弯强度和刚度影响很大。利用有限元分析软件及优化算法可对其铺层顺序和铺层角度进行优化,从而得到最优工艺方案,在原材料一定的情况下获取最大刚度,可减少材料浪费和加快设计进程。以 ANSYS-workbench为平台,利用响应面优化算法优化玻璃纤维电杆铺层角度,来提高12m高的玻璃纤维缠绕电杆的弯曲性能,加快工艺设计进程,获取最优缠绕方案,并利用优化得到的最优缠绕角度组合进行弯曲试验,获得最优刚度。电杆铺层设计中,因为层与层之间材料属性和单元方向差异较大,为了保证层间各向异性单元数据传递的准确性,层间网格采用共节点的方式进行连接。
1 原理
1. 1 复合材料本构关系
纤维缠绕复合材料可看做单层板,其力学性能不仅与玻璃纤维和基体材料性能有关,还与纤维的方向有关,是正交各向异性材料, 其应变分(εij)与应力分量(σij)的本构关系为公式(1):

1. 2 PUCK准则
目前常用的复合材料破坏准则是Hashin准则,与 Tasi-Hill、 Tasi-Wu 等准则相比,Hashin准则虽然对纤维与基体的损伤模式进行了不同方面的区分,但不能很好解释横向压缩对剪切破坏的抑制作用。但是 PUCK准则可以更好地评估预测复合材料在横向压缩和面内剪切作用下的失效情况。所以本文选择采用PUCK预测复合材料电杆的失效情况。因为缠绕电杆主要失效方式为纤维间失效,PUCK准则关于纤维间失效的3种失效模式见公 式( 2 ~5 ),PUCK准则示意图如图 1 所示。
模式 A:

模式 B:

模式 C:



图 1 PUCK准则示意图
2 电杆缠绕仿真分析
2. 1 模型建立
12m 复合材料电杆稍径为190mm;根径为350mm;锥度为1:17;杆件根部壁厚10mm,顶部壁厚15mm。12m电杆的几何模型如图2a所示;采用面网格进行网格划分,如图2b所示。

图 2 模型、 网格示意图
2. 2 材料属性
基于ansys中ACP模块建立电杆仿真模型,利用材料设计模块计算得到纤维体积比为60%的复合材料体积单元参数,并将其导入数据库作为ACP复合材料电杆铺层材料参数,具体见表1。
表 1 材料参数

2. 3 复合材料铺层设计
根据原有缠绕工艺对复材电杆进行铺层。铺设层数为 11 层, 铺层角度由内而外分别为10°、10°、80°、10°、80°、10°、80°、10°、80°、10°以及10°,铺层结构如图3所示。

图 3 铺层结构
2. 4 边界条件
将ACP模块建立的复合材料铺层模型导入静力学分析模块,设置电杆底部内表面固定约束,根据国标GB\T41491—2022, 在距离底部11750mm 处施加弯矩,具体施加位置见图4所示。

图 4 边界条件
2. 5 仿真结果
选用直接求解的方式进行电杆挠度大变形分析,如图5所示。通过数值模拟分析可得,电杆弯曲最大挠度为1270.4mm。图6为其PUCK准则IRF因子分布云图,对仿真结果进行分析可知,电杆第4层铺层在标准弯矩下可能会发生层间剪切破坏。

图 5 优化前挠度
图 6 优化前IRF因子
3 优化设计
3. 1Kriging响应面建立
本文采用Kriging算法构建优化响应面,Kriging构建的响应面通过所有设计点,拟合度较好,适用于高度非线性的复杂工程优化问题。基于Kriging法,输出参数等于全局的设计空间加上局部偏差,其表达式为:

式中,g(x)-输出参数表达式;F(α,x)-全局的设计空间函数;f(x)中上标T表示矩阵的转置;α-基函数回归系数;f(x)-变量 x的多项式函数,代表设计空间的全局模型;z(x)-均值为0,方差为σ2的高斯随机函数,其期望值和协方差分别为:

E(z(x))=0和Cov[z(x),z(u)]=σ2R(x,u, θ)(7)式中,σ2-方差;θ-相关函数的参数,用于衡量样本点t和样本点u之间相关性随两点间的距离增加的衰减度。利用试验设计的设计点形成一个相关矩阵:

式中,n-数据点总数。利用加权最小二乘法,得到Kriging模型的多项式参数:
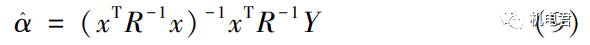
式中,x-试验设计设计点组成的系数矩阵;Y-实验设计中设计点对应的响应值。同样,方差的估计值:
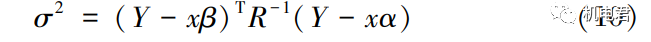
最后通过试验设计的样本点和相关函数确定基函数系数α和高斯随机方差:

最终生成Kriging响应面,其任意设计点的预测值:

3. 2 MOGA 优化
MOGA优化算法通常需要包括参数变量、约束条件和目标函数,结合挠度仿真模型建立优化模型:
1)参数变量:11层缠绕铺层角度分别为 P1、P2 …… P11, 为方便描述,命名Pα为环向铺层;Pβ为纵向铺层;P12为每种铺层方案对应的挠度值。
2)在保证复合材料电杆不会出现损伤和破坏的前提下,考虑到缠绕机的纤维缠绕极限,根据环向纵向混合铺层设定,可以确定约束条件:

3)根据弯曲模型后处理结果,设定目标函数为顶部挠度最小:

根据以上论述,进行正交试验设计,得到149组实验数据,具体见表2。基于表2数据点构建Kriging响应面,响应面如图7所示。并采用NSGA⁃II算法对所构建的响应面进行数值优化,得到5组最优解如表3。通过得到的最优解参数再次进行后处理,使其挠度值减小到1052.2mm,较优化前降低了17.33%,优化后处理结果如图8所示,并且优化铺层的IRF因子减小 到0.75,较优化前降低47.35%,优化后的IRF因子如图9所示。

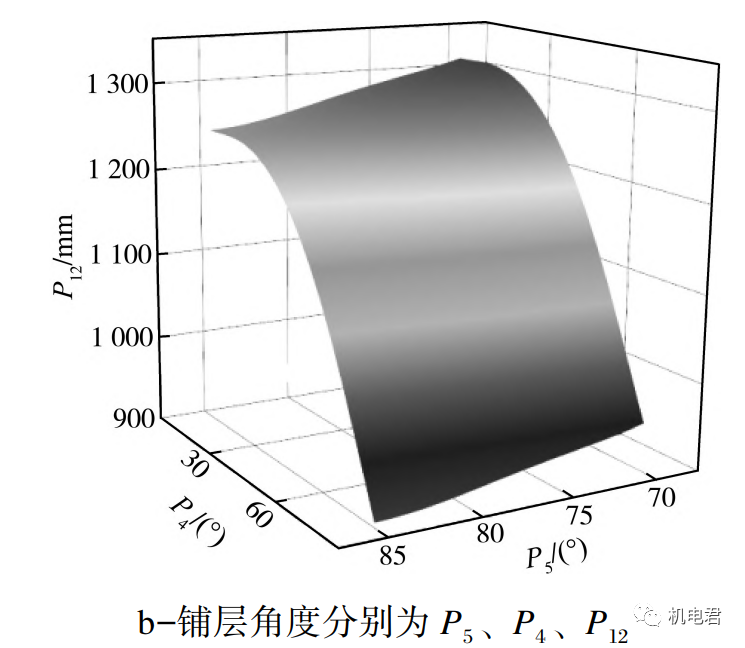
图 7 响应面示意图

图 8 优化后挠度示意图
表 2 正交试验数据

表 3 最优铺层角度示意表


图 9 优化后IRF因子
3. 3 理论验证
根据复合材料层压梁理论,假设中性面位置z=0,电线杆轴线方向为x,纯弯曲层压梁轴向弯曲模量(Ex)求解公式为:

式中,Ei(i=1,2,3)-应力主方向弹性模量;G12-剪切模量;θ-铺层角度余角;j-距离中性层的层数,N-铺层总数。计算得到铺层角度优化前后方案分别为Ef1和 Ef2,Ef1为110.02GPa;Ef2为129.84GPa。Ef2>Ef1优化后的复材电杆轴向弯曲模量Ex更大,因此刚度更大(截面惯性矩相同)。复合材料力学模型计算结果进一步证明了有限元优化模型的准确性。
4 试验
为了验证12m玻璃纤维缠绕电线杆缠绕角度优化的效果,对优化前和优化后的电杆进行了相应的弯曲试验,试验设置如图10所示。通过拉力计检测施加的弯矩载荷大小,记录标准载荷下电杆挠度,用于验证仿真结果的准确性。弯曲试验结果为:优化前电杆实际挠度为1356mm,与模拟分析结果相比相对误差为2.82%,优化后电杆实际挠度为1029mm,与模拟分析结果相比相对误差为2.0%,比优化前降低了24.11%,复合材料挠度较原始挠度大幅降低,刚度提高,如表4所示。弯曲试验与仿真模型结果拟合较好,证明仿真模型具有较高精度。

图 10 试验装置
表 4 优化前后仿真试验结果对比

5 结论
利用ACP模块、静力学分析模块和响应面优化模块相耦合的方法进行复合电杆力学分析及铺层角度优化,可替代繁杂耗材耗时耗力的玻璃纤维电杆铺层试验,获得最小挠度优化方案,从而获取最好的刚度。此类方法可节省大量人力物力和生产成本,节约产品设计周期,能够有效指导玻璃纤维电杆厂家的生产制造。




