算例丨基于ABAQUS的复合材料薄壁圆筒屈曲分析
对结构进行屈曲分析,涉及到较复杂的弹(塑)性理论和数学计算,要通过求 解高阶偏微分方程组,才能求解失稳临界荷载,而且只有少数简单结构才能求得 精确的解析解。因此,只能采用能量法、数值方法和有限元方法等近似的分析方 法进行分析。近 20 年来,随着计算机和有限元方法的迅猛发展,形成了许多的 实用分析程序,提高了对复杂结构进行屈曲分析的能力和设计水平。ABAQUS 就是其中的杰出代表。

1.屈曲有限元理论
有限元方法中,对结构的屈曲失稳问题的分析方法主要有两类:一类是通过 特征值分析计算屈曲载荷,另一类是利用结合 Newton—Raphson 迭代的弧长法 来确定加载方向,追踪失稳路径的几何非线性分析方法,能有效分析高度非线性 屈曲和后屈曲问题。

假设结构受到的外载荷模式为P0。,幅值大小为λ,结构内力为Q,则静力平 衡方程应为
λP0 = λQ
进一步考察结构在(λ+△λ)P0载荷作用下的平衡方程,得到
{[KE] + [KS(S+λ△S)] + [KG(ũ+λũ)]}△ũ =△λP0
由于结构达到保持稳定的临界载荷时有△λ,代入上式得
该方程对应的特征值问题为
det{[KE]+λ[KS△σ]+KG(△ũ)}=0
如果忽略几何刚度增量的影响,屈曲分析的方程又可进一步简化为
det{[KE] + λ[KS △ σ]} = 0
该方程即为求解线性屈曲的特征值方程。λ为屈曲失稳载荷因子,(△ũ)为结 构失稳形态的特征向量。

非线性屈曲分析方法多采用弧长法进行分步迭代计算,在增量非线性有限元 分析中,沿着平衡路径迭代位移增量的大小(也叫弧长)和方向,确定载荷增量的 自动加载方案,可用于高度非线性的屈曲失稳问题。与提取特征值的线性屈曲分 析相比,弧长法不仅考虑刚度奇异的失稳点附近的平衡,而且通过追踪整个失稳 过程中实际的载荷、位移关系,获得结构失稳前后的全部信息,适合于高度非线 性的屈曲失稳问题。

2.ABAQUS 的线性屈曲分析
ABAQUS 中提供两种分析方法来确定结构的临界荷载和结构发生屈曲响应 的特征形状:线性屈曲分析(特征值屈曲分析)、非线性屈曲分析。
线性屈曲分析用于预测一个理想的弹性结构的理论屈曲强度。它是预期的线 性屈曲荷载的上限,可以作为非线性屈曲分析的给定荷载,在渐进加载达到此荷 载前,非线性求解必然发散;它还可以作为施加初始缺陷或扰动荷载的依据。所 以预先进行特征值屈曲分析有助于非线性屈曲分析,进行特征值屈曲分析是必要 的。

3.算例

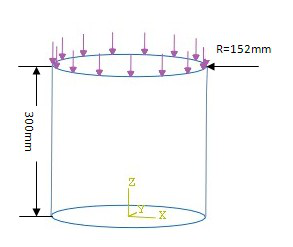
图 3-1 实例模型
如图所示两端开口的复合材料薄壁圆筒,底端固支,顶端作用有均匀分布的 轴压边载。半径 R=152mm,高度 300mm,厚度 t=0.804mm,对称铺层[±45,0]s,
单层厚度为 0.134mm。复合材料圆筒的材料参数如下表:
表 1 AS4/3501-6 石墨/环氧的弹性参数
弹性模量 | 参数 |
E1/GPa | 142 |
E2/GPa | 9.7 |
G12/GPa | 6 |
G13/GPa | 3.6 |
G13/GPa | 3.6 |
μ | 0.3 |



3.2.1 ABAQUS 进行前处理建立模型

首先先绘制一个半径为 152mm 的三维轮廓图,然后进行拉伸 300mm 创建 一个具有平面壳体单元的三维变形体。
其次进入 property 模块生成材料,参考上表编辑其弹性参数。编辑截面进行 复合层板的铺层完成材料属性、截面属性的定义。
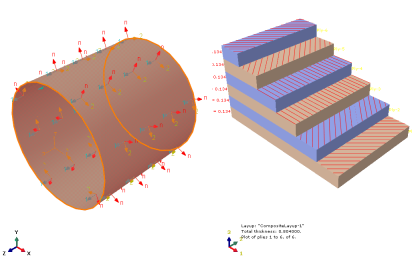
图 3-2 铺层
接着生成装配件,定义屈曲分析步。对所建模型施加边界条件和施加载荷。将圆筒的一端固支,另一端施加单位 1 的均布轴边压载。
最后进行网格划分。考虑到在复合材料层合壳模型中剪切柔度的影响,可采 用厚壳单元 S4R 来模拟它。所得到的模型如图所示:

图 3-3 模型网格图


3.2.2 计算结果分析

在 JOD 模块中建立屈曲分析模块进行分析,可得到薄壁圆筒的六阶屈曲失 稳载荷因子。
表 2 各阶模态的屈曲载荷因子
模态 | 屈曲载荷因子 |
1 | 48.015 |
2 | 48.015 |
3 | 48.98 |
4 | 48.981 |
5 | 50.188 |
6 | 50.188 |
则取第一阶模态的屈曲载荷因子计算临界载荷。由屈曲载荷因子与临界载荷的关系:
Pcr = λ ∗ p
当对薄壁圆筒施加 48.015N/mm 的边载时,圆筒将屈曲失稳。对应的各阶模态云图如下所示:
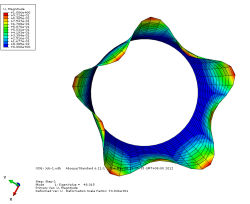
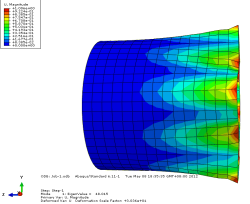
模态1位移轴向和截面方向云图
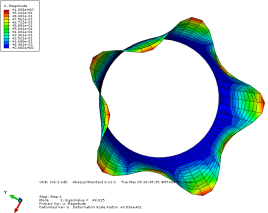
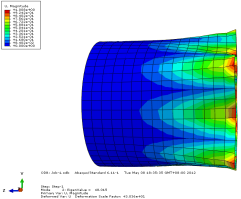
模态2位移轴向和截面方向云图
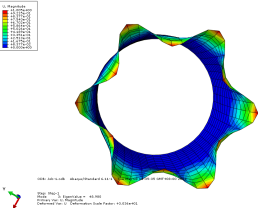
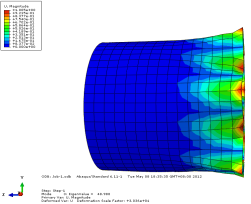
模态3位移轴向和截面方向云图
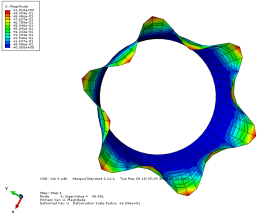
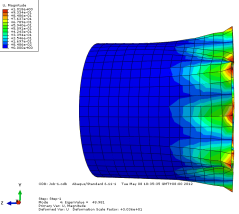
模态 4 位移轴向和截面方向云图
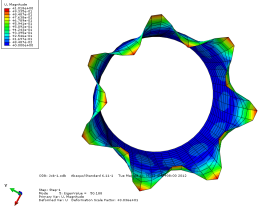
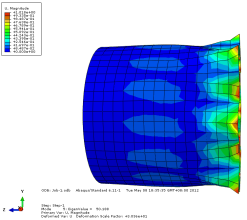
模态 5 位移轴向和截面方向云图
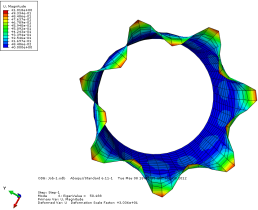
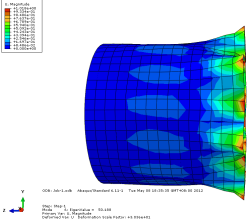
图 3-4 各阶模态云图
由上图可以看出当施加一阶模态的载荷时,圆筒已经屈曲失稳。所以保留一 阶的临界载荷更有现实意义。

4.总结




