建模与模拟验证与确认的基本理论
This title
02
作者:王瑞利 研究员
北京应用物理与计算数学研究所,北京市海淀区丰豪东路2号
引 言
This title
01
建模与模拟验证与确认的基本理论
This title
02
复杂工程M&S-V&V 基本理论涉及的内容很多,图1 给出了M&S-V&V 研究的基本框架。包括V&V 基本理论方法、V&V 方法体系、复杂工程典型物理过程M&S-V&V活动和应用程序V&V活动。其中V&V 基本理论方法涉及V&V 基本术语、概念和规范、V&V 基本方法;V&V 方法体系涉及验证、确认、评估和预测;典型物理过程M&S-V&V 活动涉及实施V&V 的流程和模板、验证与确认活动、模型不确定性量化;应用程序V&V 活动涉及实施V&V 的流程和模板、程序正确性验证技术(验证与确认活动)、程序适应性确认方法、程序可信度评估。
实际上应用程序的V&V是贯穿于M&S应用程序研制的整个生命周期。迄今为止,人们已经提出许多V&V 理论与方法,但主要工作集中在模型确认
(Validation) 方法上,而针对模型验证(Verification)的研究工作却很有限,且主要集中在计算机程序的校核上。

图1 复杂工程数值模拟程序验证与确认的基本框架
程序正确性验证技术
This title
03
3.1 方程适定性与格式基本理论验证
在复杂工程诸多应用领域,通常用偏微分方程描述物质的传播和演变规律。它涉及基于偏微分方程的M&S 理论。复杂工程的M&S 是基于偏微分方程的,涉及将定解区域作网格剖分,微分方程离散化为差分方程组及求解形成的代数方程组。为了保证计算过程的可行和计算结果的正确性,需从理论上分析离散格式组的性态,包括解的唯一性、存在性和离散格式的相容性、收敛性和稳定性。对于一个微分方程建立的各种差分格式,为了有实用意义,一个基本要求是它们能够任意逼近微分方程,这就是相容性要求。另外,一个离散格式是否有用,最终要看差分方程的精确解能否任意逼近微分方程的解,这就是收敛性的概念。此外,还有一个重要的概念必须考虑,即差分格式的稳定性。因为差分格式的计算过程是逐渐推进的,在计算第n+1层的近似值时要用到第n层的近似值,直到与初始有关。前面各层若有舍入误差,必然影响到后面各层的值,如果误差的影响越来越大,以至差分格式的精确解的面貌完全被掩盖,这种格式是不确定的,相反如果误差的传播是可以控制的,就认为格式是稳定的。只有在这种情形,差分格式在实际计算中的近似解才可以任意逼近差分格式的精确解。微分方程的适定性和离散格式的相容性、收敛性、稳定性是保证数值模拟计算结果正确性的重要前提。基于微分方程建模与模拟程序的验证与确认需以推断方程的适定性和评价格式相容性、收敛性和稳定性为目的。
对于微分方程的初边值问题是适定性。离散格式的基本理论对于单个方程已有很好的理论分析。离散格式的稳定性一般采用Taylor展开来分析,但对于方程组(如流体力学方程组)做起来比较麻烦,必须采用数值实验验证格式的稳定性。
离散格式稳定性验证技术是在固定流体力学离散格式中CFL下,通过加密网格,判断解的性态。
如在LAD2D 程序中,有三种格式:(1)E1-经典NR 格式;(2)E3-CHA 跨步走格式;(3)E5-CHA一步齐步走格式。
图2 是对平面一维Noh 问题,在粗分点(100分点)分别是E1 格式、E3 格式和E5 格式的计算结果,下图是上图在激波附近的局部放大图,每一幅图中给
出了大时间步长(CFL = 0.9)、中时间步长(CFL =0.7)和小时间步长(CFL = 0.5)的计算结果以及精确解。从图中可以看出,E1 格式由于守恒性差,计算出的激波速度偏快,而E3 格式和E5 格式计算出的激波位置与精确解基本吻合,但E5 格式大时间步长(CFL = 0.9)计算出的波后压力曲线有微扰,已有不稳定征兆。
图3 是中分点(1000 个网格) 时模型的压力分布。从图中看出,E5 格式大时间步长(CFL = 0.9)计算出的波后压力曲线有明显扰动,已开始显现数值不稳定。
图4 是细分点(10000 个网格) 时模型的压力分布。从图中可以看出,E5 格式大时间步长(CFL= 0.9)计算出的波后压力曲线震荡剧烈,中时间步长(CFL = 0.7)计算出的波后压力曲线也开始有明显扰动,可以说明E5 格式不稳定。

图2 平面一维Noh问题:精度与稳定性(100分点)

图3 平面一维Noh问题:精度与稳定性(1000分点)
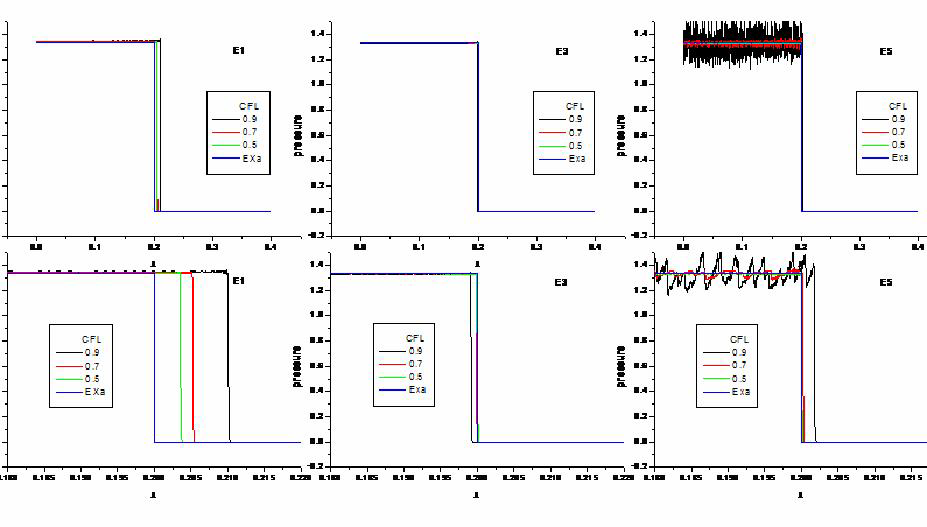
图4 平面一维Noh问题:精度与稳定性(10000分点)
图2、图3、图4 计算网格从100 到10000,在固定CFL 条件下,通过数值实验三种计算格式的数值解性态差别很大,验证E5 格式是不稳定的。这对使用格式有重要的指导意义。
3.2 定性与定量验证方法
通过一些标准的算例或试验模型,采用传统定性分析与定量比较方法,验证程序的正确性。定性方法是通过计算某个相应量值来考核模拟结果与实际系统输出或理论分析或其它程序计算结果之间的一致性,只能给出定性结论。包括云图、等值线图、矢量图、历史变化曲线和动画演示等。定量方法是给出模拟结果与实际系统输出之间的一致性的定量分析结果。包括点量、位置量、变化曲线等误差。
如图5 是LAD2D 程序计算SOD 问题定性验证结果,可以看出随着网格的加密,数值解逐渐逼近解析解,说明程序基本正确。图6 是LAD2D 程序计算SOD 问题定量验证结果,可以看出随着网格的加密,数值解与解析解之间的误差关系(马尾图),不仅可以判断程序的正确性,还可以检验程序离散格式的精度。

图5 网格尺度从0.1~0.025(16套)计算与解析对比

图6 网格尺度从0.1~0.025(16套)计算与解析的误差统计分析的马尾图
3.3 软件测试验证技术
程序设计是问题求解中的实践活动。正如任何问题求解活动一样,确定解的有效性是这一过程的一部分。软件测试是贯穿于M&S应用程序研制整个生命周期的验证技术。
3.3.1 软件测试在软件研制各阶段中的任务
软件测试的各项活动一般平行并稍后于软件研制过程的各阶段。因为,在软件研制早期对错误的发现和更正要比在后期发现和更正花费少,并且可使软件的质量和可靠性得到显著提高,以保证软件研制的正确性。对应于软件研制的各个阶段,软件
测试的任务可分别简述如下。
(1)需求分析阶段
此阶段对应于软件研制概念形成阶段的文档,如软件需求规格说明书、软件立项报告等进行独立的审查评估。通过对软件需求的独立审查与推导,与标准参照系统的比较,功能模拟,研究软件系统的使用情景分析,验证软件的需求。对软件需求规
格说明进行可追踪性分析,制定软件系统测试计划,确定验收测试要求,进行测试软件流程设计,起草测试计划书。
(2)物理数学方案阶段
此阶段对应于软件研制物理方程与数学离散形成阶段的文档,如软件研制物理方案、软件研制数学方案等进行独立分析、推导与测试。通过对方程适定性与离散格式的相容性、收敛性、稳定性分析与测试,验证方程与离散格式的正确性。
(3)软件设计阶段
在软件的概要设计与详细设计阶段,对设计所确定的功能、算法、数据结构、接口进行推导、分析,包括模拟、与标准件进行比较等,验证软件的设计,保证软件各功能间的作用是合理恰当的。
(4)软件编码阶段
在软件实现,即编码与单元测试阶段,展开编码分析和独立的单元测试,包括版本比较、文法和句法分析,标准化审查,公式再造,数据结构分析,流程图分析,逻辑的重建,人工代码走查,界面分析等,验证代码中实际的和潜在的缺陷。进行编码分析要充分使用工具,与编码同时进行,以提高软件的可见性。独立的单元测试主要检查软件的作用范围是否在所要求的范围内,并完全覆盖;对模块及接口进行正常与极端条件下的双重测试。这一阶段要随时(通过软件配置管理)纠正编码中的错误,并验证新增代码。
(5)软件测试阶段
进行软件功能模拟测试和检查。要起草软件测试报告,对软件正式文本中的异常加以描述,说明软件的程序源代码分析与测试的结果。
(6)软件验收阶段
这个阶段的测试要建立软件在系统使用环境下的可信度,在系统集成过程中,独立地完成集成测试,与开发者和用户一起进行系统联试和验收测试,给出软件研制工作的最终评价报告(或证书)。
(7)软件使用及维护阶段
该阶段软件测试的任务是在软件的安装、调试、使用和维护过程中,保证系统受到配置控制。在软件交付时,向项目管理组织提交测试问题报告,提出安装调试、配置管理、系统运行的第三方评价。
3.3.2 数值算法验证
数值算法验证关注的是如何正确地程序化数值算法,以及数值算法本身的精确度和可靠性。数值算法验证的主要目的是提供充足的证据来证明程序化的数值算法执行正确且有预期的功能。数值算法验证关注的焦点是程序数值算法的正确性。常采用
精确解方法、人为解方法和高精度程序解比较等方法或手段。
精确解比较方法。很早以前就采用非常简单的精确解来验证计算模型。选择的精确解一定要包括足够多的结构,使得方程中的所有项,以及离散化中产生的所有误差项都能体现出来,因此,分析和鉴别好的、敏感的精度估计算例是非常重要的。在
捕捉激波格式的研究中,计算流体力学界就经常选用Riemann问题等来验证和确认计算方法的精度。
这些问题的主要特征都是在一定的条件下,精确解内包含间断,就如同气体动力学中的激波和接触间断,因此对这些模型问题中间断的计算精度就代表了计算方法模拟真实激波问题的计算精度。人为构造解比较方法。人为构造解方法是精确解方法更加一般化、简单化的替代技术。它是一种逆向思维验证程序的方法。它的基本过程是针对程序求解的偏微分方程(组)先假设一个(组)解,将这个解代入原方程(组),推导并确定使方程(组)能够成立所必须添加的源项以及边界条件。然后在数值求解的应用程序中增加源项以及边界条件下,数值求解原来的偏微分方程(组),得到数值解,这个数值解是假设精确解的近似,两个解之间进行比较,就可以确定程序的误差或误差。目前对于欧拉流体力学方程组,构造了大量光滑人为解,且有些人为解得特点是质量守恒方程和能量守恒方程得源项为零,对高维计算程序可以方便的检验数值算法实现过程的缺陷,能严格验证程序数值算法的正确性。但对于带有间断问题,人为构造解方法是非常困难的,且人为构造解方法解是不含有物理意义的。
3.4 解法(方法)验证
解法(方法)验证主要思想是用数值模拟结果与精确解、人为构造解和高精度数值解进行比较,量化其数值误差及不确定度。该方法的核心是进行网格收敛指标验证来确定实际的收敛阶,通过分析对比实际的收敛阶与理论上的收敛阶来判断程序是
否存在错误或缺陷。另一方面是通过对数值模拟影响因素进行敏感性分析,以达到辨识和量化误差、不确定度和置信度。即数值模拟验证包括方法理论/网格收敛指标验证与计算敏感性分析。
3.4.1 网格收敛指标验证技术
任何流体力学问题都要受一些物理学定律所支配,比如质量守恒定律、动量守恒定律和能量守恒定律等。对于非定常流动,这些物理学定律形成了初边值问题;而对于定常流动则形成了边值问题。
一个初边值问题可由基于这些物理学定律所建立的一组连续偏微分方程及初边值条件所定义。数值求解是在流体力学初边值问题的基础上,通过数学解析的方式获得其解析值。虽然解析的过程可能是精确的,但为了能获得解析解,不仅要对流体力学初边值问题进一步简化,而且有可能要对几何模型和边界条件进行大量简化,从而必然会产生与真实值的差异,导致很大的建模误差。
基于偏微分方程的初边值问题,解析求解往往是很困难的,必须数值求解。数值求解的方法是通过采用数值技术,把连续的初边值问题转化为离散的初边值问题,即通过使用空间和时间离散技术(比如有限差分、有限体积和有限元等),近似地求解初边值问题。从而导致由于空间间隔Δx 和时间间隔Δt 等产生的数值误差(即:当这些间隔趋于零时,数值误差是零)。这样在进行数值求解时,可能会产生的数值误差。包括网格尺度误差、时间步长误差、迭代误差,以及一些输入参数所引起的误差等。开展程序正确性验证,必须辨识网格尺度误差、时间步长误差、迭代误差和输入参数误差等数值模拟结果的可接受性,正确考虑由于网格尺度所产生的误差和不确定性。
量化各种误差和不确定度,常采用网格收敛指标(Grid Convergence Index,GCI)验证技术。GCI主要是采用Richardson 外推法建立了估算网格误差的方法。常用的做法是针对计算问题,建立多套计算网格,多套网格原则上要求自相似,既体现Δt 和Δx为逐渐缩小的趋势,然后通过计算L1、L2、L∞范数,进行网格收敛性分析来确定实际的收敛阶。这种做法常常需要知道问题的精确解或采用固定不变的网格,对定常问题或单独考核格式的精度是一种行之有效的方法。
网格收敛指标验证技术的核心是要对模拟问题有一个对比解。基于爆炸波问题,在LAD2D 程序上尝试了GCI 验证技术。

计算采用CFL=0.5,一次粘性系数取0.06,二次粘性系数取0.2。图7 给出了50~900 个网格单元间隔10 的14 套网格(分点依次为50、60、70、80、90、100、200、300、400、500、600、700、800、900)计算到t 0.1时计算结果与数值解析解的比较。通过GCI 验证技术,可以看出LAD2D 程序在计算强激波问题时,随着网格的加密,数值解逐渐逼近解析解,说明程序的正确性。
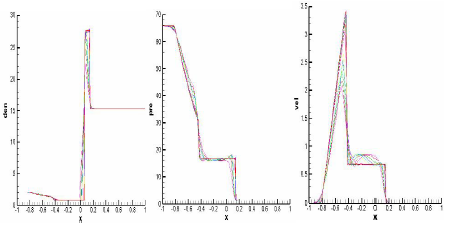
图7 网格尺度从0.04~0.025(14套)计算结果与解析解的对比
基于人为构造解方法,针对流体力学方程组构造了一类光滑人为解。考虑有源项的理想流体控制方程和状态方程:




从上面基于解析解、人为构造解方法,实施网格收敛指标验证,不仅可以判断程序求解的正确性,更重要的是验证了算法的精度,以说明数值模拟程序的可行性。
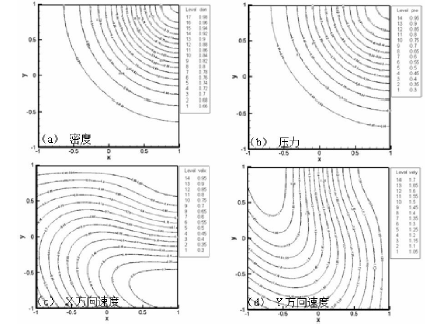
图8 人为解与计算对比(实线:计算;虚线:人为解结果)例子

表1 网格收敛指标验证
3.4.2 敏感性分析验证技术
利用典型物理问题作为分析模型,并结合已有的实验信息,分析论证数值模拟计算结果中由于计算模型、计算参数、数值方法等引入的不确定度。以及数值计算中网格参数(网格类型、尺度和规模等)、计算格式和参数(时间步长、粘性等)、计算过程中的误差时空演化特征分析等。一般用概率与非概率方法辨识与量化误差、不确定度和置信度。
一般情况下计算敏感性分析与网格收敛指标结合,能将误差、不确定度和置信度。主要采用在计算条件变化的情形下对同一被模拟量进行多次抽样即复现性数值模拟分析方法。目前,用累计分布函数(Cumulative Distribution Function,CDF)方法可以量化数值计算的误差和置信度,此方法的优点是既能综合分析所有误差源,又能通过概率分布函数给出数值计算误差的不确定度。CDF 是对连续函数,所有小于等于a 的值,其出现概率的和为F(a)=P(x<a)。图9 给出了应用CDF建立的爆轰计算误差、网格尺度和置信度的马尾图。采用了10 套(100、200、300、400、500、600、700、800、900、1000)网格。从图上可以看出网格尺度与计算误差、置信度的关系。如假设要求爆轰计算的误差在2%,密度置信度要求达到0.9,那么可以从图9 看出,网格尺度必须小于0.02(500 个分点以上)。通过此方法能非常清楚的给出爆轰计算的置信度。

图9 网格尺度从0.1~0.01(10 套)计算到
t =0.8μs结果误差统计分析的马尾图
3.5 程序功能验证技术
复杂工程M&S 的程序正确性验证技术除了推断格式是否正确离散方程(方程与格式)、程序是否正确实施(算法与代码)外,软件的功能是否达到用户要求也是验证程序的一个重要活动。有时人们总是认为这一部分属于M&S 确认的活动,实际上这一部分也包含了程序实施正确性的问题。为了测试复杂工程流体力学程序的功能,逐渐完善发展内爆动力学过程程序验证的评价基准数据库。为了验证复杂工程流体力学程序的功能,逐渐完善建立了内爆动力学过程程序验证的基准模型库CFDCTM(如图10)。包括CFDCTM_A 库(基本应用模型库)、CFDCTM_B库(基本理论模型库)。测试模型包括模型基本理论、模型结构、基准解(解析解、实验数据或高精度数值解)。CFDCTM_A库包括爆轰波、Noh 问题、壳球对称模型、平面爆轰、圆筒实验、绕爆模型、应力波问题、Taylor 杆、旋转问题、间隙模型、侵彻实验、简化内爆问题与RT不稳定模型、一点起爆内爆模型等13 类测试模型,CFDCTM_B 库包括简单波、8 种1D 黎曼问题、19 种2D 黎曼问题、激波通过气泡的问题、前后台阶问题、双马赫反射问题、Sedov 点爆炸问题、SALTZMAN 位置问题、密封容器内外爆问题、飞片撞击实验模型、钢球冲击铝靶、简化内爆与区域分割模型、聚能射流问题、水下爆炸问题等14 类问题。为开展M&S 程序功能验证提供重要的依据。

图10 CFDCTM 库内容
另外,结合M&S-V&V 技术方法,逐渐发展M&S-V&V 的分析软件工具包。
问题与展望
This title
04
本文给出了应用程序M&S 的V&V 的含义,明确验证与确认的基本内容,着重描述了复杂工程M&S 程序正确性验证技术。
(1)方程适定性和格式相容性、收敛性、稳定性是保证数值模拟计算结果正确性的重要前提。对于复杂工程应用程序,必须开展格式稳定性验证。其次通过一些标准的算例或试验模型,采用传统定性分析与定量比较方法,验证程序的正确性。
(2)测试是贯穿软件的研制的整个生命周期。在不同阶段测试有不同的含义,必须引起研制者的高度重视。
(3)需要结合应用领域的特点,发展数值分析、网格收敛指标验证技术、偏微分方程(PDE)精确解析解、半解析基准解(Benchmarks)、高精度基准解、人为构造解,以及软件质量保证等程序正确性测试验证技术。