技术 tips 2 | 常微分方程学生包] - 自动显示微分方程的分步求解过程细节
上期介绍了如何用Maple求解微分方程,本期内容给大家介绍Maple 2021新增加的Student[ODEs]微分方程学习包,该学习包可以自动显示计算步骤和详细结果,与以前版本中的微积分、线性代数、数值分析学习包一起辅助老师教学和学生自学。
Student[ODEs]
命令:ODESteps
功能:显示ode、ivp或odes的分步求解过程
学习包命令ODESteps支持以下类型的ode和odes:
• 一阶常微分方程
• 一阶IVPs常微分方程初值问题
• 二阶常微分方程
• 二阶IVPs常微分方程初值问题
• Cauchy-Euler 方程
• 级数解
• 特殊函数解
• 常微分方程系统
初始值问题常微分方程系统
示例1
非齐次一阶常系数线性微分方程:
Diff(u(x), x) = c*u(x) + x^2
restart;
with(Student[ODEs]);
ode1 := Diff(u(x), x) = c*u(x) + x^2;
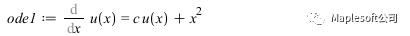
ODESteps(ode1); #显示计算细节

示例2
with(Student:-ODEs);
ode2 := diff(y(x), x) - y(x) - x*exp(x) = 0;

ODESteps(ode2);

示例3:一阶IVPs
restart
with(Student:-ODEs);
ivp1 := {t^2*(z(t) + 1) + z(t)^2*(t - 1)*diff(z(t), t) = 0, z(3) = 1};

ODESteps(ivp1);

示例4:二阶ODEs
restart;
with(Student:-ODEs);
ode4 := 2*x*diff(y(x), x) - 9*x^2 + (2*diff(y(x), x) + x^2 + 1)*diff(y(x), x, x) = 0

ODESteps(ode4)

示例5:二阶IVPs
with(Student:-ODEs);
ivp5 := {diff(y(x), x, x) - diff(y(x), x) - x*exp(x) = 0, eval(diff(y(x), x), x = 0) = 0, y(0) = 1};

ODESteps(ivp5) #显示计算细节

示例6:Cauchy-Euler方程
with(Student:-ODEs);
ode6 := x^2*diff(y(x), x, x) - 4*x*diff(y(x), x) + 2*y(x) = 0;

ODESteps(ode6)

示例7:级数解
restart;
ode7 := x^2*diff(y(x), x, x) + x*diff(y(x), x) + 5*x*y(x) = 0

Student:-ODEs:-ODESteps(ode7)

示例8:特殊函数解
restart
with(Student:-ODEs);
ode8 := x^2*diff(y(x), x, x) + 4*x*diff(y(x), x) + (25*x^2 - 9)*y(x) = 0;

ODESteps(ode8)

示例9:常微分方程系统
restart
with(Student:-ODEs);
high_order_ode1 := diff(y(x), x, x, x) + 3*diff(y(x), x, x) + 4*diff(y(x), x) + 2*y(x) = 0;

ODESteps(high_order_ode1)

示例9:Systems of ODEs with IVP
restart;
with(Student:-ODEs);
high_order_ivp1 := {diff(y(x), x, x, x) + 3*diff(y(x), x, x) + 4*diff(y(x), x) + 2*y(x) = 0, eval(diff(y(x), x), x = 0) = -1, eval(diff(y(x), x, x), x = 0) = 2, y(0) = 1};

ODESteps(high_order_ivp1)





