趣味问题1:球从A点到B点,走曲线更快!---abaqus中的最速曲线研究
本文摘要(由AI生成):
本文首先引用了张小娴的《世界上最遥远的距离》来探讨距离的概念,进而转向讨论“世界上最近的距离”在物理学中的最速曲线问题。作者通过abaqus软件模拟了小球沿不同路径滚下的实验,验证了最速曲线(旋轮线)并非直线,而是使物体从高处到低处运动时间最短的路径。这一理论在仓储物流等领域有实际应用,文章通过实际模拟展示了最速曲线的原理和应用,对abaqus软件的应用也提供了新的思路。
《世界上最遥远的距离》
张小娴
世界上最遥远的距离 The furthest distance in the world
不是生与死的距离 is not the way from birth to the end.
而是我就站在你面前It is when I stand in front of you
你却不知道我爱你 but you don't understand I love you.
....
那“世界上最近的距离”是什么呢?,我们在中学的时候,老师就告诉我们两点之间的直线距离最短。好像也是这么回事。那么是不是从点A到点B,走直线也最快呢?
好像我提出了一个很牛逼的问题啊,有木有,有木有!!
“伽利略的棺材板压不住啦!”
经过多位牛人的研究,一个球从高处A,到低处B点,速度最快的线,不是直线,而是一条摆线,也叫旋轮线。旋轮线与1673年荷兰科学家惠更斯讨论的摆线相同。因为钟表摆锤作一次完全摆动所用的时间相等,所以摆线(旋轮线)又称等时曲线。
它长这个样子:
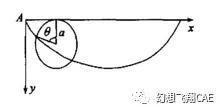
看不懂没关系,我用abaqus给画了一下,就变成这个样子了
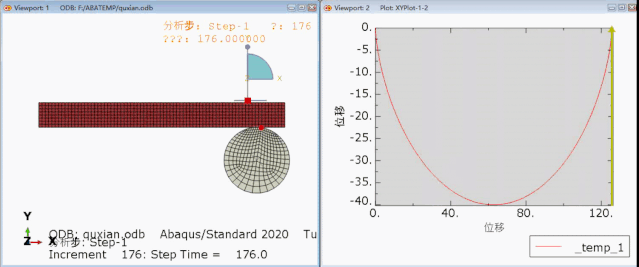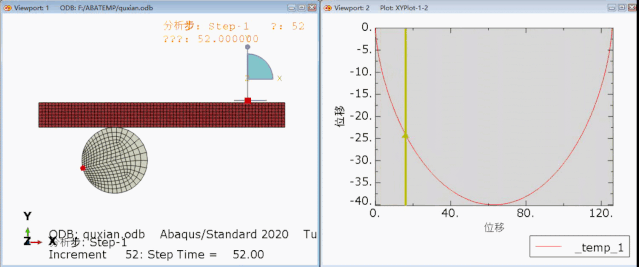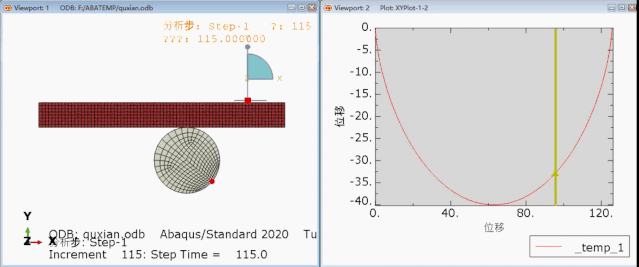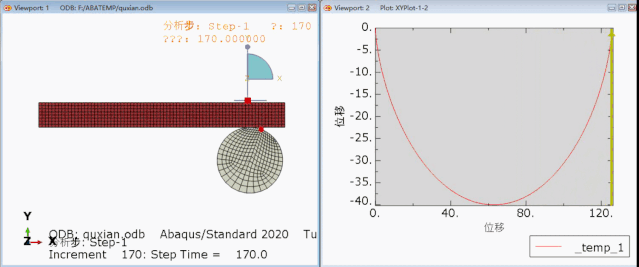
这是一条非常优美的曲线啊,有了这条曲线,我们就可以研究最速曲线的问题了。作为严谨的我来说,必须要有对比分析才可以。
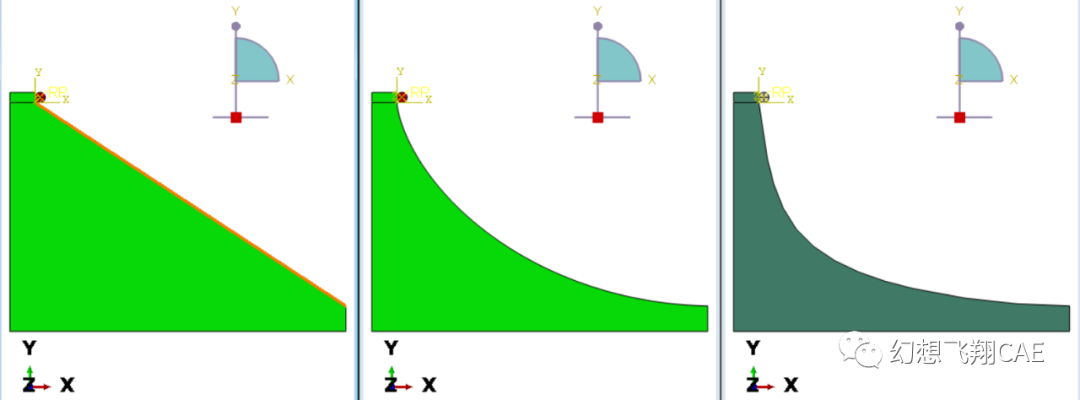
(从左到右分布是:斜面,最速曲线,对比曲线)
我们分别建立三个模型,然后在顶部放了一个小球。让它只受重力作用,摩擦力为0.然后手一松,往下滚。

红色小球的曲线,就是最速曲线,它也是第一个到达终点!
关于最速曲线的解释呢,有很多。选取一种:
其物理原理为在同一高度滚下的两个球, 两球下滚的原因都是受重力分力的作用, 沿直线下滚的球, 下滑的加速度保持不变, 速度稳定地增加。沿着旋轮线下滑时, 开始的一段的坡度非常大, 使得下滑的球在非常短的时间内取得的下滑速度非常大。虽然, 在下滑的后半阶段, 坡度逐渐变小、速度增加变缓, 但此时的下滑速度已经变得很大。所以, 沿着旋轮线下滑在整个下滑阶段的平均速度很大。即使旋轮线的长度比直线的长度大, 沿着旋轮线下滑的时间也比直线短。
例如,最速降线理论在粮食仓储物流中有广泛的应用, 在解决仓储工艺和设备上可发挥重要作用, 如改善空气斜槽、溜管和布粮器等设备的性能参数, 优化粮食仓储工艺等
本次利用abaqus的显式求解分析,完成了最速曲线的整个流程,验证了前人的结论,对abaqus的应用,也起到了一定的启发作用。是一次非常有意思也非常有意义的尝试。





