克努森数与连续介质
1 克努森数的概念
克努森数(Knudsen number)定义为分子平均自由程和空间尺度的比例:
克努森数的取值决定了物理问题的类型及其适用的方程。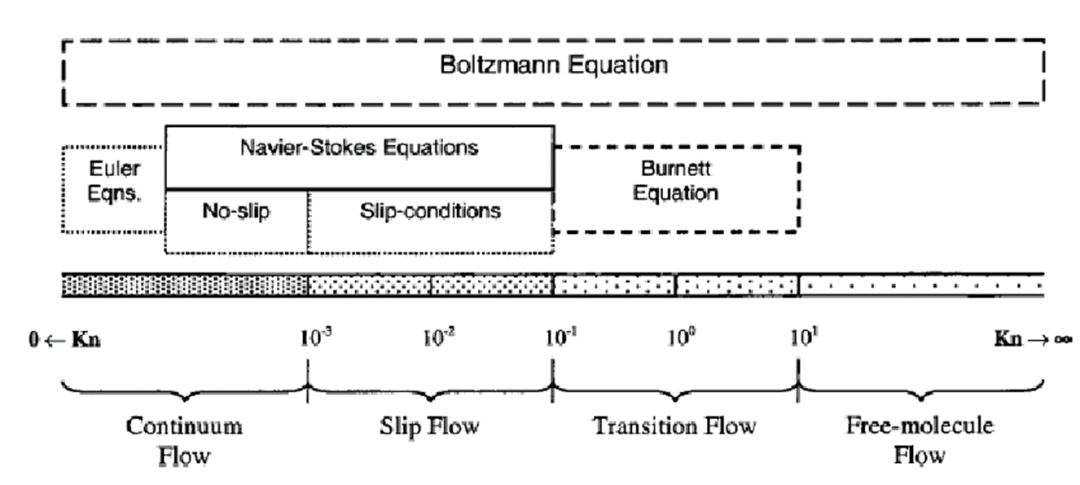
各方程对应的克努森数适用范围(图源:researchgate.net)
2 大克努森数的案例
在大克努森数下(Kn>0.1时),需要使用DSMC(Direct Simulation Monte-Carlo)求解玻尔兹曼方程。此时,连续介质前提假设已经不满足,N-S 方程已失效,无法使用有限体积法、有限单元法等方法求解 N-S 方程的方法进行分析。在文献《Continuum and kinetic simulations of the neutral gas flow in an industrial physical vapor deposition reactor》(《Surface and Coatings Technology》期刊)中,作者对物理气相沉积(PVD)问题进行了不同解法的对比:1 利用 ANSYS Fluent 通过有限体积法求解 N-S 方程
2 利用修改版 dsmcFOAM(OpenFOAM的模块)通过 DSMC 求解玻尔兹曼方程
PVD 设备如图所示,其内部绝对压力约为 500 mPa,温度 300 K,气体介质氩气、氮气。
A:入口
B:阴极电极
C:样品
D:加热器
E:出口
将 dsmcFOAM 结果的分子能量分布做统计,其整体能量分布状况符合麦克斯韦-玻尔兹曼能量分布曲线。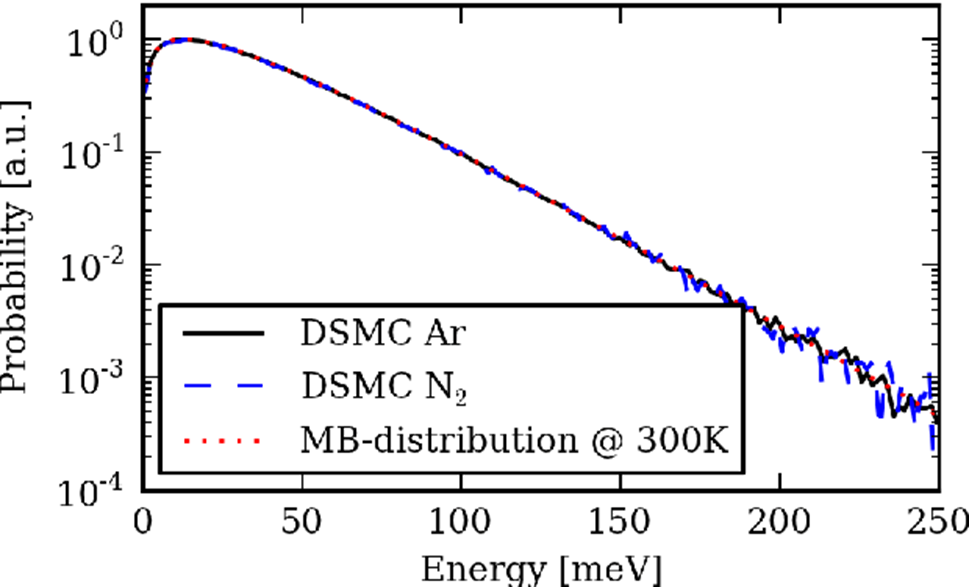
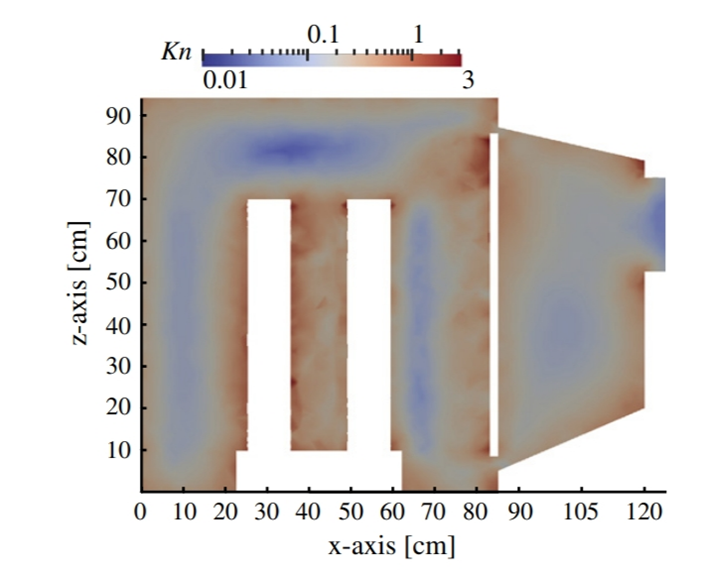
截面上克努森数分布如图所示(分子平均自由程取氩气在500mPa时的1.39cm),数值远超过无滑移边界条件 N-S 方程要求的 0.001 的上限。
对比 dsmcFOAM 和 Fluent 结果,压力分布如图所示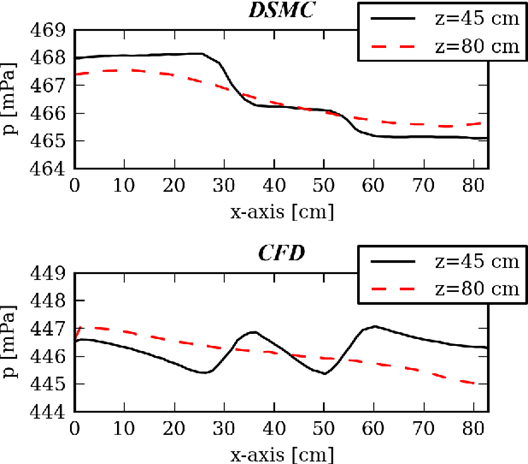
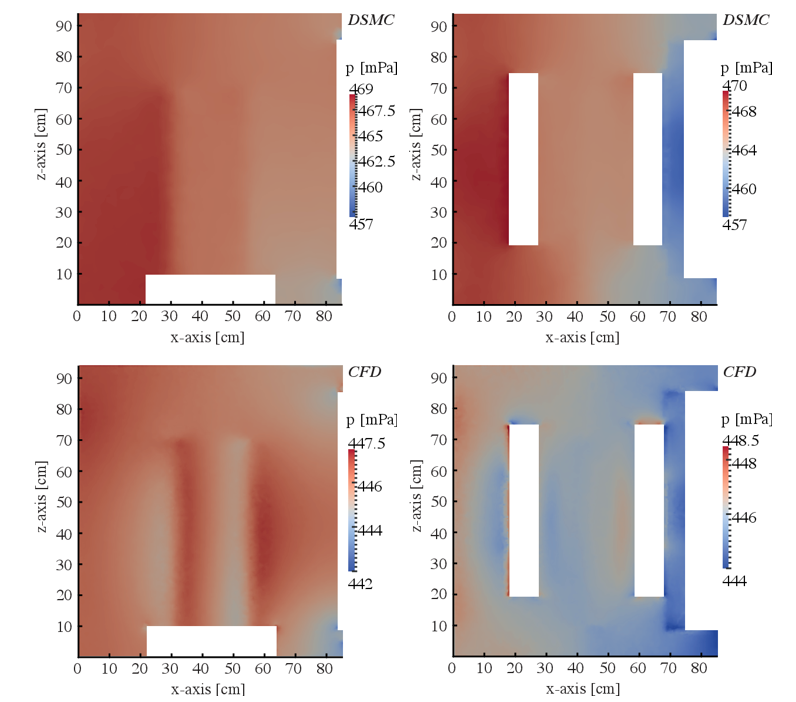
对比 dsmcFOAM 和 Fluent 结果,流线如图所示
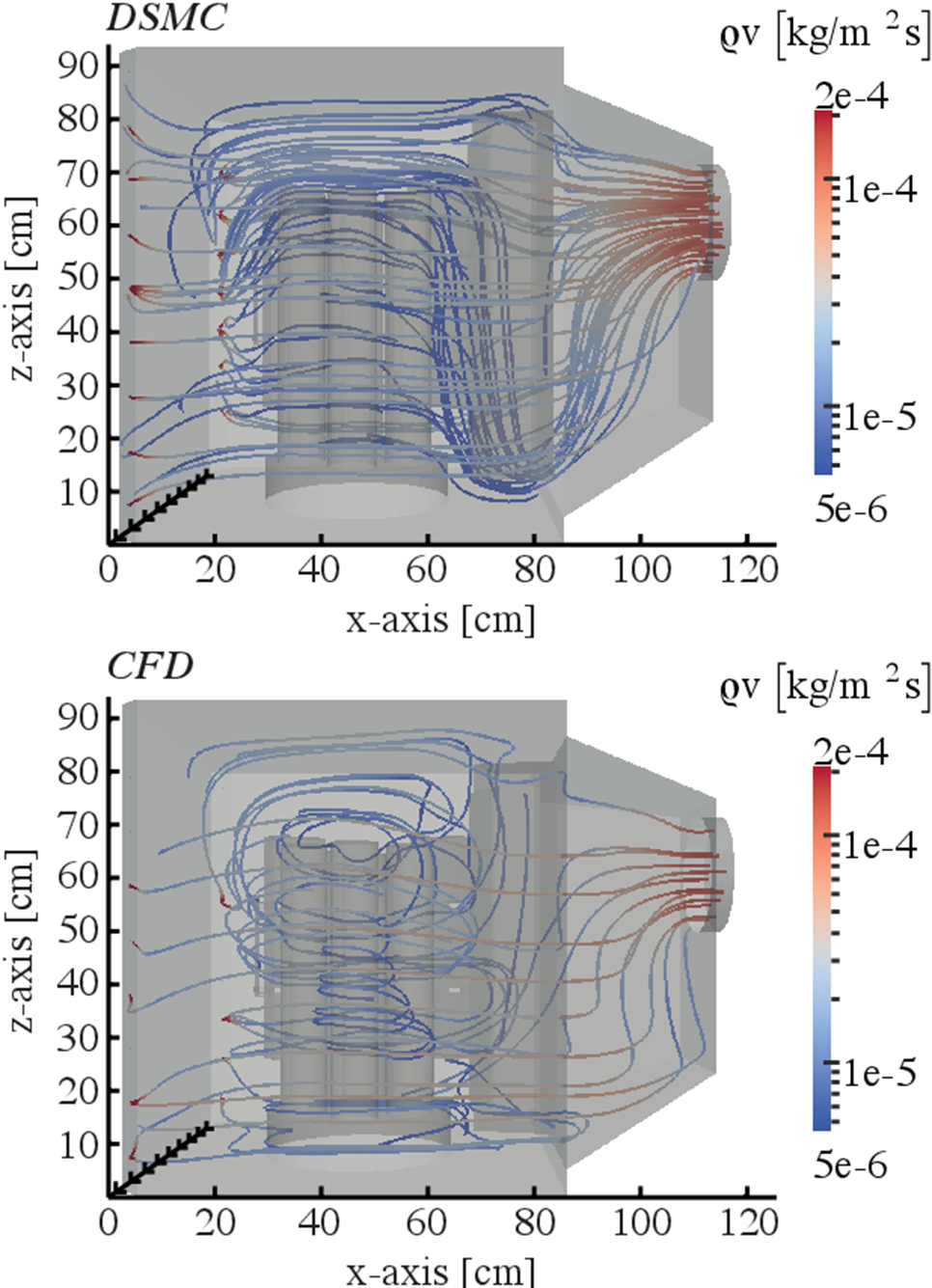
从对比结果看,两者的仿真结果差异较大,基于 N-S 方程的结果在大克努森数问题中已经难以满足准确性要求。












