算例丨Abaqus软件中陶瓷本构模型及侵彻损伤失效数值计算应用实例
陶瓷是一种典型的脆性材料,可采用Wilkins、Rajendran-Grove、Johnson-Holmquist(JH)和Deshpande-Evans本构模型描述其在高应变率加载下的响应情况,其中JH模型是目前数值计算领域应用最为广泛的陶瓷本构模型,如图1所示。JH-1本构模型是Johnson和Holmquist于1992年提出的第一个脆性材料的本构模型,采用分段函数的方式描述了脆性材料压力和强度的关系(JOHNSON G R, HOLMQUIST T J. Shock Wave and High Strain Rates Phenomena in Materials, 1992: 1075-1081);JH-2模型(1999年)在JH-1模型基础上进行了归一化处理,并将描述压力和强度的分段函数写成了连续函数(JOHNSON G R, HOLMQUIST T J. Journal of Applied Physics, 1999,85(12): 8060-8073);为能更好的描述AlN陶瓷在高应变率下的响应,2003年Johnson、Holmquist和Beissel在JH-1模型的基础上考虑了材料的相变特性,提出了JHB模型(JOHNSON G R, HOLMQUIST T J, BEISSEL S R. Journal of Applied Physics, 2003,94(3): 1639-1646);2005年Johnson和Holmquist两人给出了确定JHB本构模型参数的过程,并基于试验结果给出了校准后SiC陶瓷的JHB本构模型参数(HOLMQUIST T J, JOHNSON G R. Journal of Applied Physics, 2005,97(9): 93502)。
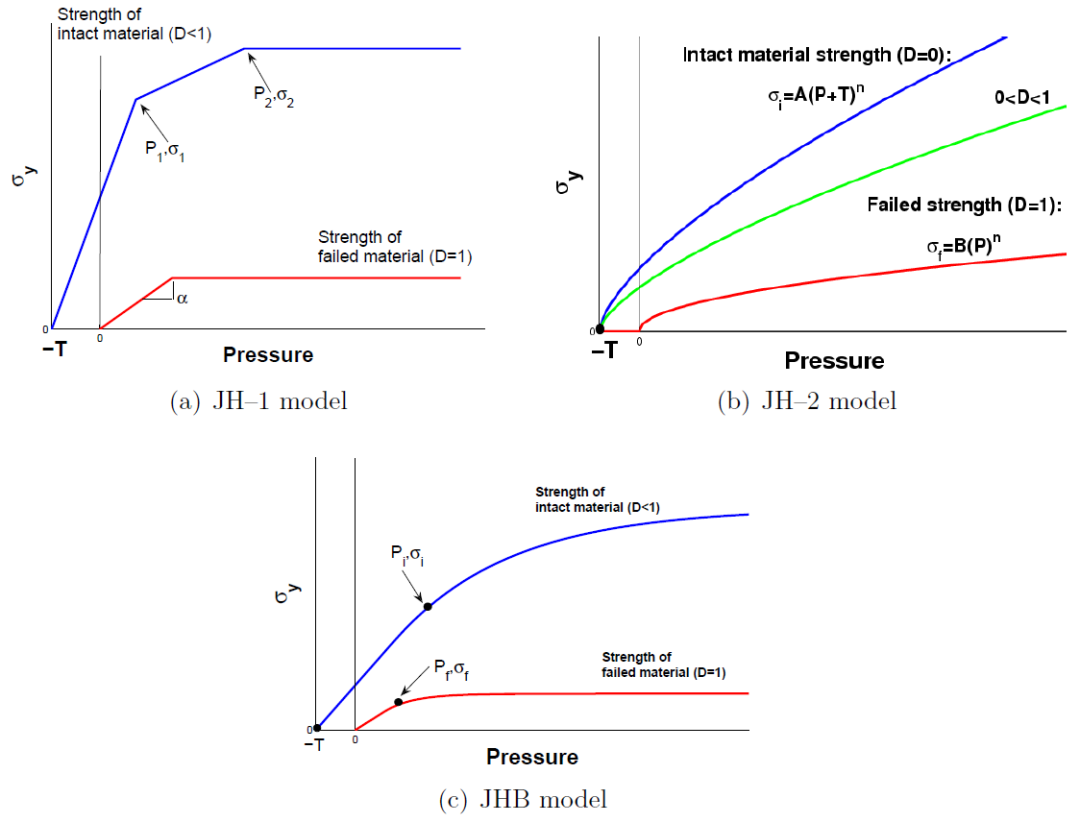
图1 3种JH陶瓷本构模型
虽然Johnson、Holmquist等人对陶瓷的本构模型开展了大量的研究,将陶瓷材料的响应分为完整和失效两种状态,但实际加载时应力状态较为复杂,通过JH本构模型反映其损伤失效过程仍较为粗糙。现有的JH本构中,弹性未损伤段参数多为根据试验数据得出,但陶瓷损伤失效段参数则多为根据试验结果拟合得出。1 数值计算软件中本构模型
陶瓷由于其波速高、模量大,具有良好的抗侵彻性能,在各类型装甲设计中被广泛应用。而JH本构形式简单,易于理解,已成为Abaqus、LS-DYNA和Autodyn等商用软件的内嵌本构模型,可一定程度上满足日常使用及工程计算要求。对于陶瓷材料Abaqus帮助中给出了3种本构模型,Extended Drucker-Prager本构(以下简称DP本构)、JH-2和JHB本构模型。DP本构多用来模拟岩土材料(粒状土壤和岩石),扩展DP本构给出的应力与压力的关系也与JH本构中未损伤时应力与压力的关系类似,其损伤段定义采用等效塑性应变与应力三轴度的对应关系进行定义,状态方程采用Mie-Grüneisen形式(详见Abaqus相应部分帮助)。Abaqus官方帮助中给出的JHB本构模型参数如表1所示。其中标红部分与Abaqus帮助(2021版本)不同,应为帮助原文疏漏。表1 JHB本构模型参数
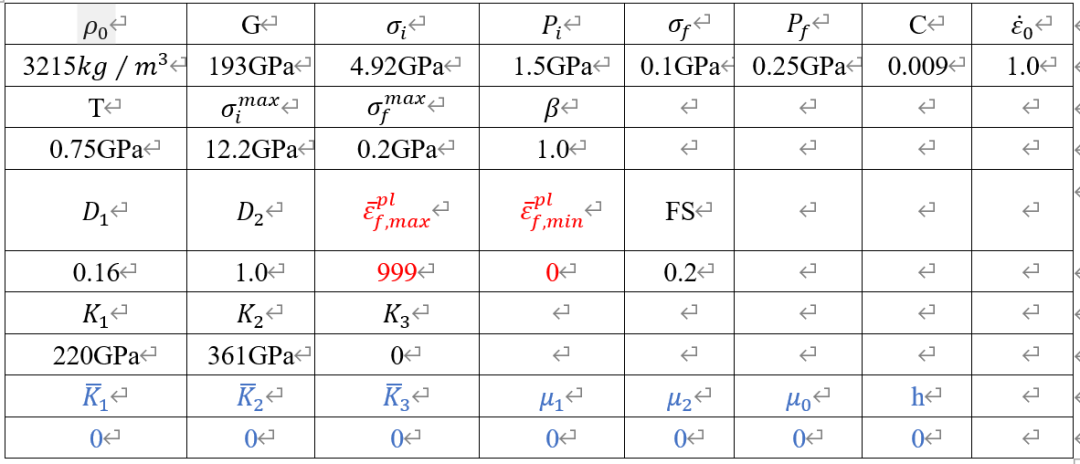
JHB本构模型的应力与压力关系主要分为完整(Intact)和损伤(Failed)两部分,表1中下标带有 i 的即为完整部分相应参数,下标 f 即代表损伤部分参数;虽然JHB本构模型公式中考虑了脆性材料的相变特性,表1标蓝部分参数应为对应的相变参数,但帮助中全部设置为0,推知官方帮助中给出的这组参数不能考虑陶瓷相变的影响。Abaqus官方帮助中给出的JH-2本构模型参数如表2所示。表2 JH-2本构模型参数
JH-2本构模型以无量纲形式描述了应力和压力的关系,以Hugoniot极限下的压力对压力变量进行了无量纲化。JH-2本构中SDV7为体应变,SDV8为材料点状态MpStatus,与JHB本构相比不输出SDV7最大体应变,其余6项状态变量(SDV)与JHB相同。
2 数值模型
模型为半径5mm、长度10mm钨合金棒材侵彻边长50mm、厚6mm的陶瓷板四分之一模型,如图2所示。侵彻速度1000m/s,模型整体进行四分之一边界约束,边界面全部节点铰支。所有单元为C3D8R单元,单元最小尺寸为0.25mm。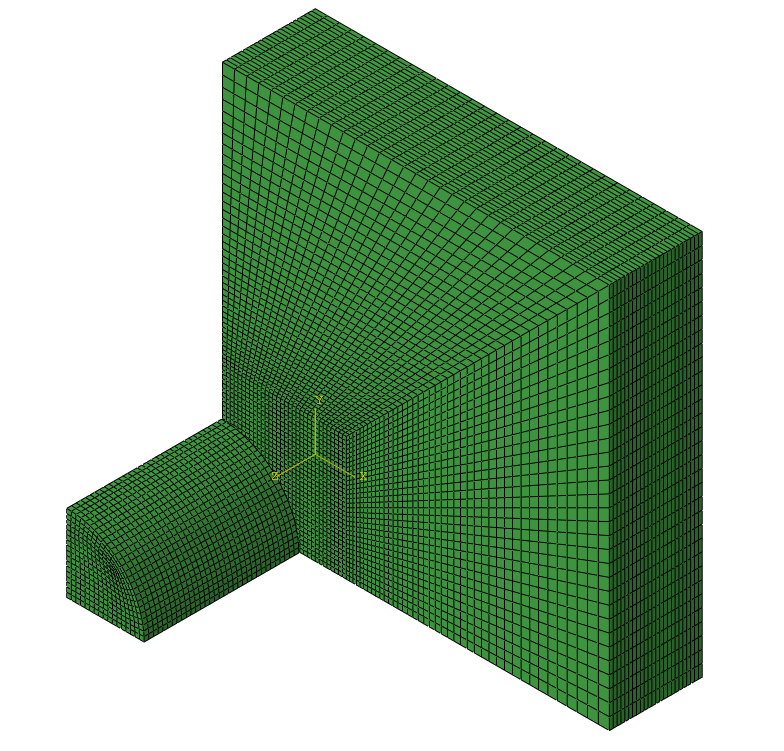

为对比不同本构模型的求解同一问题的差异,仅修改inp文件中本构模型参数部分,提交计算,Abaqus2021版本求解器单精度8核并行求解。3 结果讨论
官方帮助中长杆金棒侵彻半无限陶瓷靶板时,金棒的侵彻深度随时间的变化情况与试验值基本一致,如图3所示。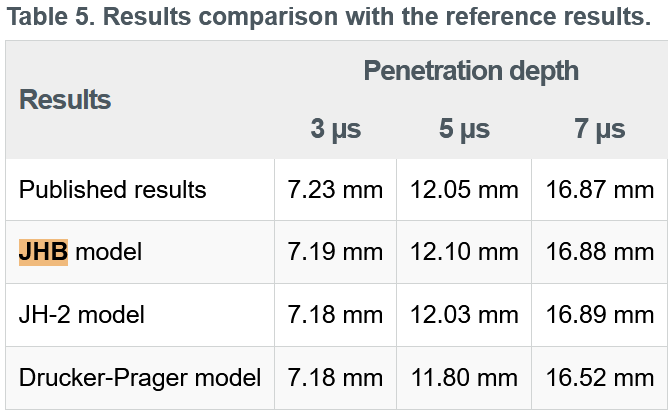
3种陶瓷本构模型参数保持不变,求解第3节中的工况。图4为使用3种不同本构模型时棒材尾端点速度降情况。由图可知,0.015ms左右棒材已经穿透陶瓷板,速度基本保持不变,但陶瓷板使用JHB本构后棒材速度降约比其它两种本构模型高150m/s,与DP和JH-2本构计算结果差别较大。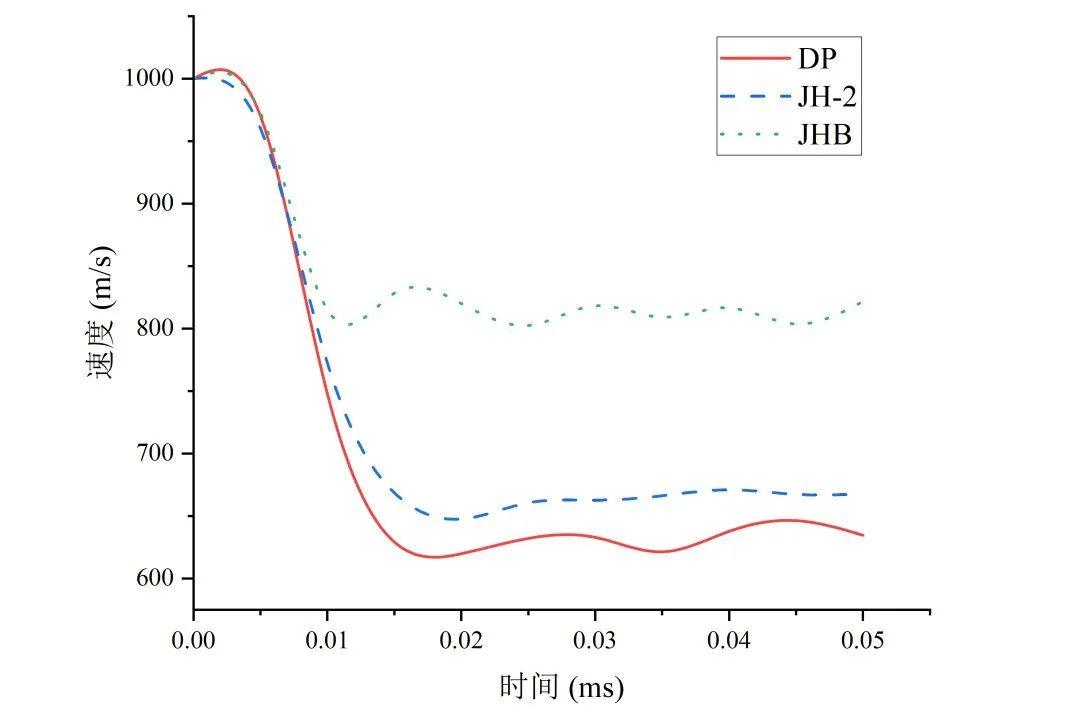
图5为0.02ms时陶瓷板的破碎情况。使用DP本构的陶瓷板环裂不明显,陶瓷锥明显;使用JH-2本构的陶瓷板环裂明显,陶瓷锥较为明显;使用JH-2本构的陶瓷板无环裂和陶瓷锥出现,其主要原因是陶瓷单元过早删除。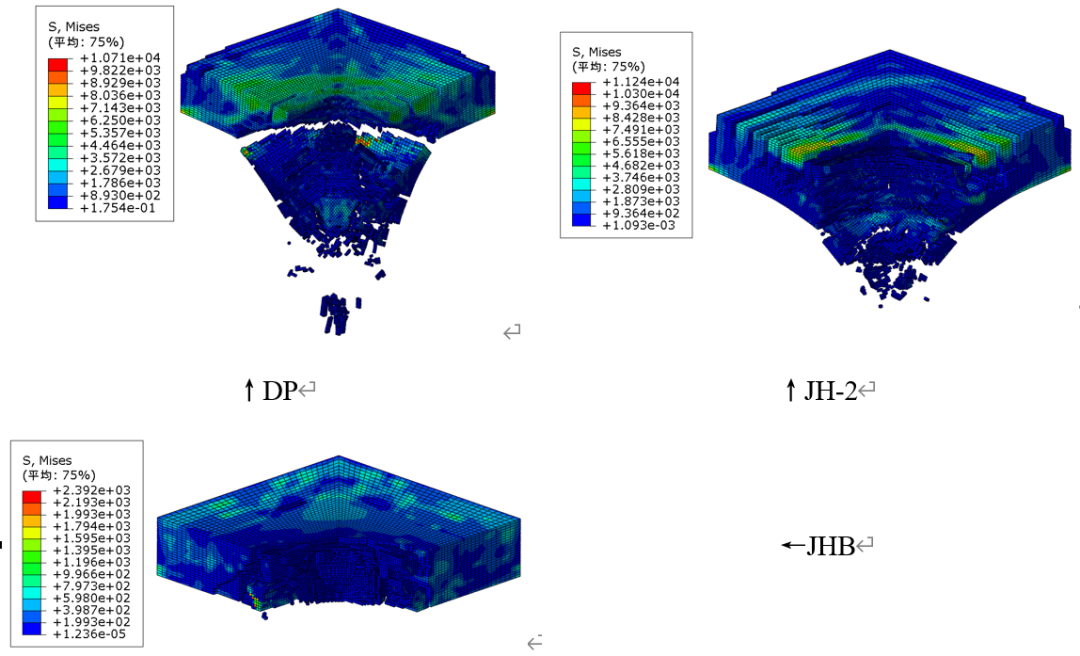
3.2 分析与讨论
由4.1节中数值计算结果可知,JHB本构模型的求解结果与另2种本构模型结果的存在明显差异。其主要原因是不同本构模型定义陶瓷材料的损伤失效模型存在一定差异,造成了JHB本构模型单元失效快,棒材速度降低。而陶瓷本构的损伤段参数往往都是根据试验拟合得出的,不能适应所有的工况,故调整JHB本构的损伤段参数,进行重新求解,结果如图6所示。此时速度降基本与其它两种本构模型一致,且陶瓷破碎出现陶瓷锥及环裂现象。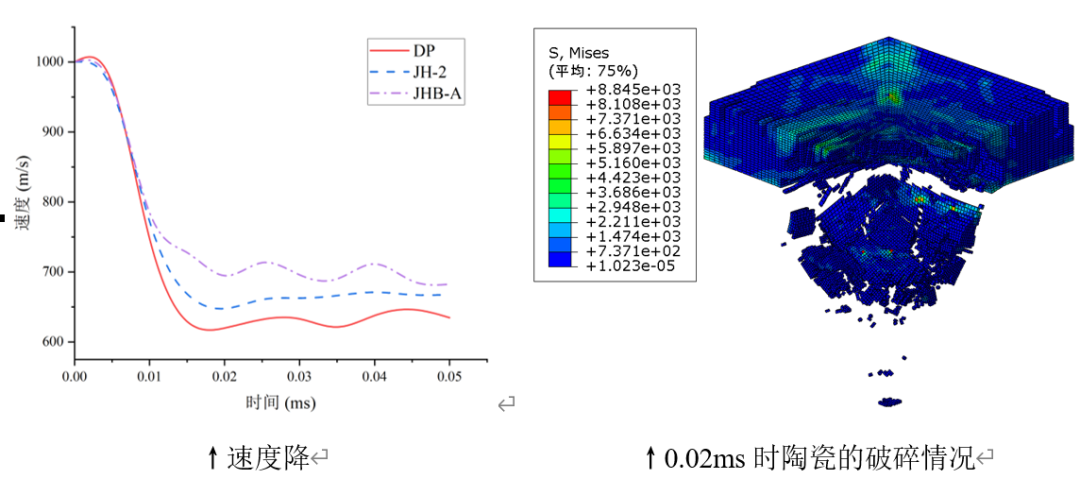
根据3种本构模型的损伤失效公式可知,本质上DP和JH-2本构是一种累积损伤失效模式,即理解为不同的损伤程度对应不同的应力压力关系曲线,在损伤过程中对应的曲线是不断产生变化的,变化的过程是连续函数;而JH-1和JHB本构模型在不同损伤程度时,仅对应两种状态,即完整和失效两种状态,类似数字电路中的0、1,是不连续的间断函数。JH本构模型本质上是一种唯象本构模型,是通过观察到的现象来确定公式形式、耦合参数的。陶瓷的高应变率的损伤失效行为是在微秒级甚至更小的时间尺度内发生的,JH本构模型通过较为简单的公式很难精确反映其损伤失效过程。故采用单元失效来表征材料失效的方法难以对这类复杂的侵彻问题进行求解,如需得出较为准确而可靠的数值计算结果,在目前本构模型的基础上,还应诉诸于以SPH为代表的粒子法处理这类问题。JH本构对求解的边界条件敏感,改变单元的大小、整体的分布趋势(如加密方式不同)及单元属性(如四面体网格)等都将对计算结果造成影响。最后,在实际工程实际使用当中,个人认为没必要考虑哪种本构更精确更可靠,其实它们"半斤八两;,选择自己熟悉且合适的本构模型即可。当使用一个本构模型一直不能求解出满意结果时,也不妨换个本构模型尝试一下。 













