你需要了解的RC低通滤波器
滤波电路是我们在设计电路时随处可见的,尤其是简单的RC低通滤波器,我们在信号输入、输出都会随手放置一个;因为太常见,反而我觉得自己理解得不深刻,今天好好学习总结下。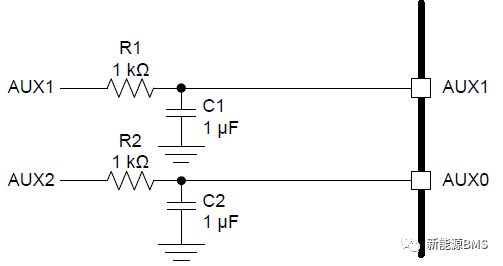
滤波器是指一个电路,它能够去除掉人为指定的某个频率范围的信号分量;因为模拟信号的频率分量很丰富,但我们只想要其中一小部分内容,其他的对我们来讲都是噪声,滤波器就是用来滤除噪声的。滤波器分了好多种,低通滤波器LPF是其中的一种。(图片来源于网络)
标准答案为:当保持输入信号的幅值不变,通过改变输入信号频率,当出现输出信号降至输入信号幅值的0.707倍(-3dB)时,此时对应的频率称为这个滤波器的截止频率。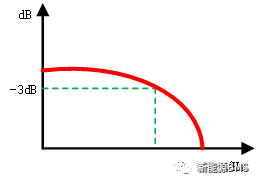
这里插一句,在电子电路中,使用分贝dB来表达增益,例如电压、电流增益,功率增益,它是一个表征相对值大小的量;具体的计算公式为下式对数形式,注意功率增益前面是X10,而电压、电流为X20。
然后实际验证一下截止频率下的增益:20lg(0.707)=-3.011dB,结果正确。由无源元件(电阻、电容、电感)组成的滤波电路,称为无源滤波电路,典型的RC低通滤波器如下:
它的截止频率计算如下(公式不容易显示,所以改成图片):
在时域中分析RC电路,更多使用时间常数,而在频域中,则更多使用截止频率。验证仿真一下,在下图中,电阻为1KΩ,电容为1uF,根据上面公式可以得到它的截止频率为159Hz。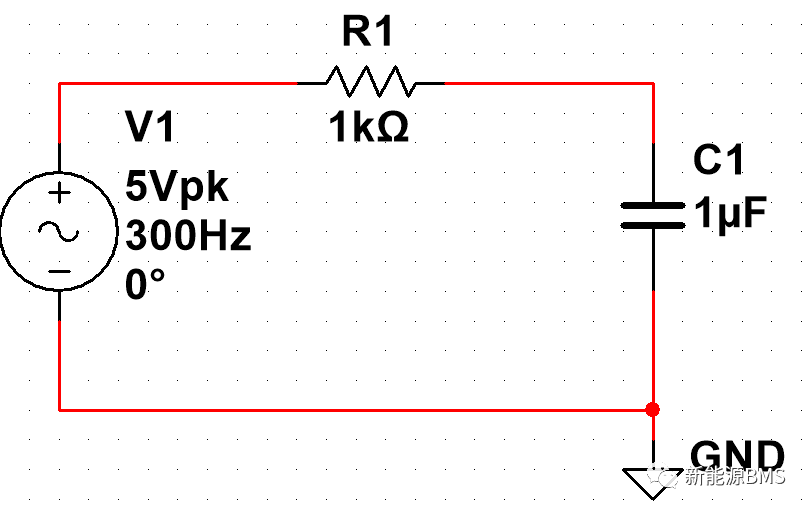
然后看一下它的波特图:从下图中可以清晰看见,在频率159Hz处,对应的增益正好为-3dB;另外,截止频率右侧的增益逐渐降低,代表随着频率升高,滤波器对信号幅值的衰减作用。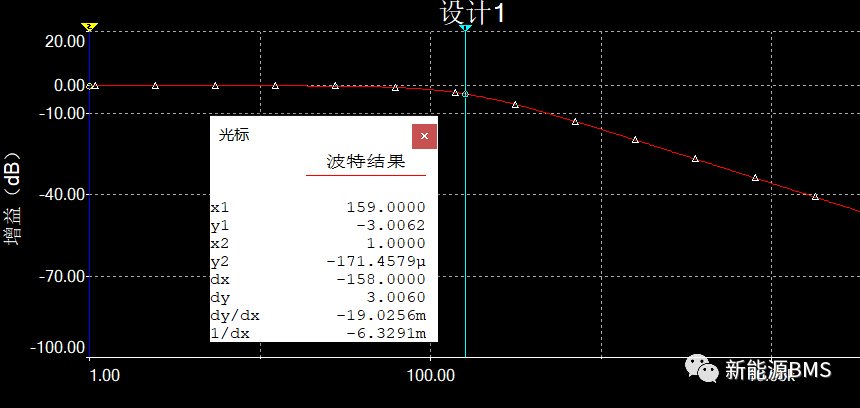
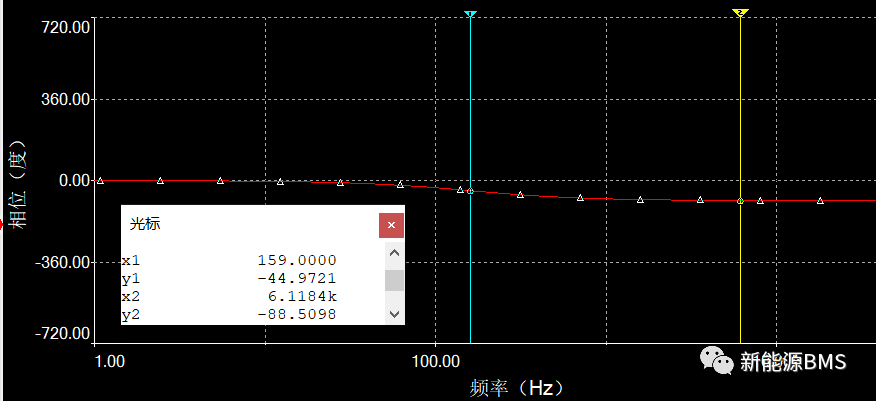
在使用RC低通滤波器时,我们要清晰知道它的截止频率,是否会影响我们想要的信号幅值。下图为300Hz的正弦波输入信号,以及经过上面RC滤波器后的输出信号,发现幅值和相位发生了明显变化。
下图为30Hz的正弦波输入信号,以及经过上面RC滤波器后的输出信号,发现只有相位发生了变化,幅值基本没有被影响,这两个例子明显看出来滤波器在起作用。
再深入一些,其实正弦波是一个特例,我们看一下30Hz的方波信号,输入输出如下图所示,发现输出信号波形发生了明显改变。
这是因为,虽然方波信号在时域中看起来是一个单纯的30Hz周期信号,但是它的频谱分量却很丰富(可以看一下傅里叶级数展开),实际上包括了许多高频信号,所以在经过同一个滤波器后,高频分量被滤除,波形自然就发生了变化,而正弦波的频谱比较单纯。这次主要提到了一阶LPF,实际还有二阶、三阶等等,高阶可以实现让波特图中的过渡时间更短,更接近理想的滤波器,但也就更复杂;以上所有,仅供参考。 著作权归作者所有,欢迎分享,未经许可,不得转载
首次发布时间:2023-08-26
最近编辑:1年前























