【分析知识】非线性分析中若干重要概念的解读

每个人都会累,没人会为你承担所有的伤悲和疲惫,所以总有那么一段时间你要学会自己长大,困难和苦难从不会一直是成长路上的绊脚石,有时候它也会变成垫脚石!

1. 什么是线性和非线性分析?
如果在分析过程中,外载荷与模型的响应之间为线性关系,去掉载荷后,模型能够恢复至初始状态,这就是一个线性分析,其特点是:
【1】几何方程的应变和位移的关系是线性的;
【2】物理方程的应力和应变的关系是线性的,满足胡克定律;
【3】根据变形前的状态建立的平衡方程是线性的;
【4】可以满足叠加原理。
上述四条中如果有一条不满足要求,就必须进行非线性分析。
2. 非线性分析的三种类型?
【1】几何非线性:即位移的大小对结构的响应发生影响,包括大位移、大转动、初始应力、几何刚性化和突然翻转等问题。
【2】材料非线性(一般指弹塑性分析):即材料的应力应变关系为非线性。
【3】边界条件非线性(接触分析):即边界条件在分析过程中发生变化。接触问题就是一种典型的边界条件非线性问题,其特点是:边界条件不是在计算的开始就可以全部给出,而是在计算过程中确定的,接触体之间的接触面积和压力分布随外载荷变化,同时还可能需要考虑接触面间的摩擦行为和接触传热。
3. 几何非线性开关的作用是什么?在何时应将其打开?
几何非线性开关将决定在分析过程中是否考虑几何非线性对计算结果的影响。如果在某个分析步中会出现大位移、大转动、初始应力、几何刚性化或突然翻转等问题,就需要在这个分析步中将几何非线性开关打开(Large Deflection),否则,即使分析能够顺利完成,得到的结果也是错误的;如果模型不会出现几何非线性,就不需要打开大变形开关,否则会大大增加分析的收敛难度。
当做几何非线性分析时,由于几何缺陷会对结构的响应发生影响,因而需要打开大变形开关;弹塑性分析(材料非线性)的时候如果模型的位移较大,则需打开大变形开关,而当位移不大且对结构响应没影响的时候则不需要打开大变形开关,即弹塑性分析的时候可能伴随着几何非线性或不需要考虑几何非线性。
4. 分析步:初始分析步和后续分析步?
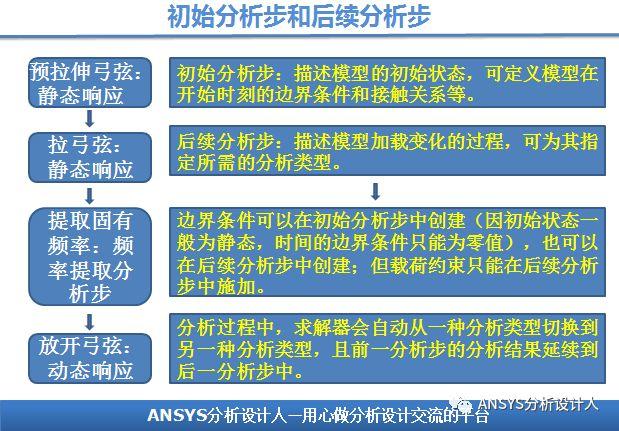
一个复杂的有限元模型往往包含一系列相互关联的事件,可以根据事件发生的先后顺序,一个模型可以由一个或多个分析步构成,用来描述一系列相互关联的事件;ANSYS中为这些事件分别定义相应的分析步,各个分析步的分析类型可以使不同的, ANSYS会自动选取相应的求解器进行计算。例如,模拟弓箭发射的过程就可以定义4个分析步:
【分析步1】预拉伸弓弦-静态响应;
【分析步2】拉弓-静态响应;
【分析步3】提取固有频率-频率提取分析步;
【分析步4】放开弓弦-动态响应。
初始分析步:ANSYS自动创建的一个分析步,而且一个分析模型中只有一个初始分析步,不可以被重命名、编辑、删除等。
后续分析步:可以定义一个或多个后续分析步,来描述模型加载变化的过程。每个后续分析步都需指定所需分析类型。如上述弓弦分析过程的静力分析 瞬态分析及动态分析。
5. 增量步和迭代的概念?

【1】增量步:对于非线性问题,位移和载荷的关系是非线性的,因此无法一次完成整个分析步的求解,这时就需要将整个分析步分解为多个增量步来依次求解,沿着非线性响应的变化路径逐步得到整个分析步的最终响应。
【2】迭代:在一个增量步中寻找平衡解的尝试称为“迭代”。如果当期解满足了平衡条件(达到收敛),则此增量步计算结束,并开始求解下一个增量步;如果当前解不满足平衡条件,将会进行下一次迭代,继续寻找平衡解。
【3】因分析的时候采用迭代分析,每一分析步可能包含若干增量步,每个增量步可能需要进行若干次迭代收敛,若增量步中迭代不收敛,可能需要减小增量步继续迭代。初始增量步的设置会影响到计算时间和收敛性,一个增量步若经历16次迭代仍不收敛,则会将增量步减小到原增量步大小的25%进行求解,且允许进行5次折减,如果增量步经过5次折减仍不收敛,则不需要再减小增量步,此时不收敛往往不是增量步大小的原因了,而是模型本身或边界条件设置的问题导致的;同时,一个增量步若连续两次在5次迭代以内就收敛了,可将增量步大小增大到原值的150%,以达到节省计算时间提高计算效率的目的。
6. 初始增量步、最小和最大增量步的含义及设置方法?

【1】初始增量步:初始增量步中的的载荷大小=总的载荷大小×(初始增量步时间/分析步总时间)。对于很容易收敛的问题,令初始增量步为1即可;对于难以收敛的非线性问题,(例如模型中有复杂的接触或大的塑性变形),如果在第一个分析步中就把全部载荷施加在模型上,使接触状态发生剧烈的改变,分析步不容易收敛,可以尝试减小初始增量步(如分析步时间乘以0.1或0.01)。静态分析中,如果模型中不包含阻尼或与速率相关的材料性质,“时间”就没有实际的物理意义,方便起见,一般都把分析步时间设为默认的1。如果初始增量步设置的较小,会大大增加增量步数,延长计算时间;如果设置的太大,分析会很难收敛,ANSYS将不得不进行多次折减,反复减小增量步,同样会浪费大量的计算时间,甚至会出现无法收敛而中止计算。所以计算时间和计算精度永远是两个矛盾体,取决于操作人员对理论知识和计算模型的灵活把握。
【2】最小增量步:一般情况下使用分析步时间乘以10-5次方即可。对于非常复杂的非线性问题,可以再将其减小1~2个数量级,太小则没必要。不收敛问题往往是模型本身存在问题,仅仅减小最小增量步并不能真正解决问题。
【3】最大增量步:它对模型是否收敛没有影响,一般情况下采用默认值(等于分析步时间即可)。
对于非线性分析深入理解上述几个重要概念并能够在操作过程中灵活设置,对于解的收敛性和计算效率的提高都会有很大的帮助,上述内容部分参考专业书籍总结,与朋友们共同学习!


