随着产品设计的规模和复杂性持续增长，使用 Abaqus（有限元分析 （FEA） 和多物理场工程仿真软件）进行分析评估的计算资源需求越来越高。结构的全局分析可以首先用于确定对荷载的响应至关重要的区域。然后可以为关键区域创建局部子模型，并改进几何或网格细化。此局部子模型提供了比全局模型更高的精度，而无需重新划分网格和重新分析整个模型。这种方法可以降低分析成本，同时在关键区域保持足够的细节。本文将介绍子模型的理论，Abaqus 中可用的两种子模型技术，以及如何实现子模型。我们还将重点介绍 Abaqus 中子模型的局限性以及验证分析结果的重要步骤。
子模型理论
Abaqus 中的子模型利用 Saint-Venant 原理，即子模型的边界足够远离子模型中的感兴趣区域，以允许将施加的力替换为等效的局部力。全局模型求解用于通过控制代表所施加力的因变量来定义子模型边界的行为。只要端部荷载保持静态等效，感兴趣区域中的解就不会因端部效应而改变。
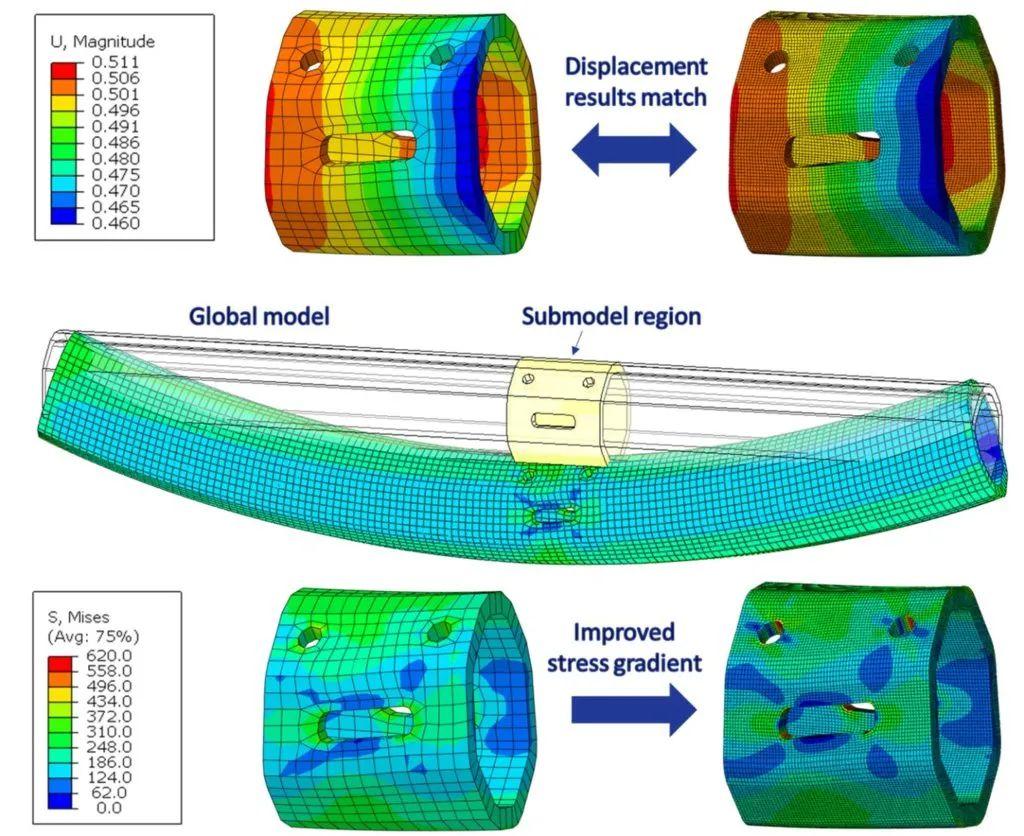
在图1中，显示了具有多个局部开口的梁模型。梁的全局模型用于确定驱动变量作为子模型公共边界处的输出，并有助于使用相对粗糙的网格。分析在全局模型和子模型上独立执行，因变量是两者之间的唯一链接。通过这种独立性，可以灵活地更改几何特征、元素类型、材料属性等，以改善子建模区域的表示。与任何建模技术一样，验证结果以确保它们在物理上有意义非常重要。比较全局和子模型的子模型区域边界附近的等值线图可用于确认结果是否一致。
Abaqus的子模型技术
在 Abaqus 中，有两种技术可用于子建模，称为基于节点和基于曲面的子模型。基于节点的技术将全局模型中的节点结果字段插入到子模型节点上，这是更通用和常用的技术。相反，在基于曲面的子模型中，应力场值传到子模型曲面积分点上。基于曲面的子建模仅限于实体到实体的应用和静态分析，对于所有其他目的，应应用基于节点的子建模。根据模型的属性，可以在分析中使用任何一种技术或两者的组合。
在静态分析中，如果子模型区域的平均刚度存在显著差异，并且全局模型受到力控制载荷，则基于曲面的技术可以提供更准确的应力结果。然而，当区域中的刚度相当时，基于节点的子建模将提供与基于表面的子建模类似的结果，同时降低由刚体模式引起的数值问题的可能性。刚度差异可能是由于子模型中的附加细节（例如开口或圆角）或微小的几何变化（无需重新运行全局分析）造成的。
如果模型承受大位移或旋转，则基于节点的子模型可以提高将大位移和旋转传递到子模型时的精度。取决于最感兴趣的输出结果。基于节点的子模型将在提供更准确的位移场传输。而基于表面的子建模将提供更准确的应力场传递，从而更准确地确定子模型中的反作用力。这两种技术可以包含在不同边界的单个模型中。
Abaqus 子模型的实现
在生成子模型前，必须先进行全局模型分析。在图 2 中，定义子模型边界的集 合以红色突出显示，并标记为子模型区域。
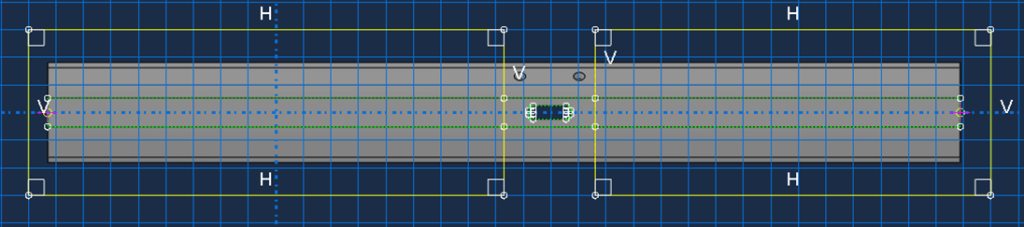
所有类型的荷载和边界条件都可以应用于子模型。但是，应注意以与全局模型一致的方式在子模型中应用载荷和边界条件，以避免不正确的结果。只有因变量将值传递到子模型。任何预定义字段都必须像在全局模型中一样提供。全局模型和子模型之间的初始条件应一致。为简单起见，复 制初始全局模型以创建子模型（图 3）会很有帮助，使用创建切割工具去除子模型边界之外的材料，如图 4 所示。此方法将允许保留全局模型设置，并最大程度地减少创建子模型时出错的可能性。
分析部必须与全局模型设置一致。在子模型边界条件设置时，指定驱动节点，你可以指定某些自由度为驱动节点-通常所有自由度都作为驱动节点。如图5，制定了子模型的边界条件及驱动节点自由度。应注意的是只有基本变量可以作为驱动，如位移，温度，电势等。子模型边界条件像其他边界条件一样可以创建，修改或删除。
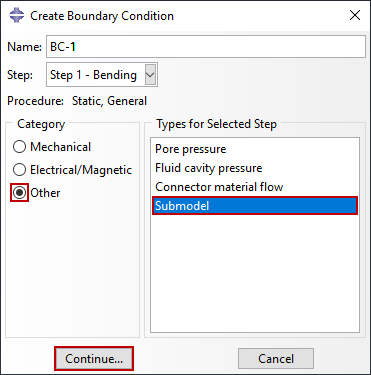
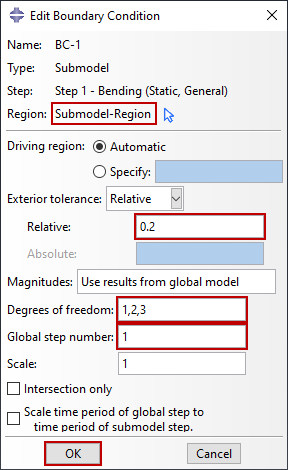图5 子模型边界条件当全局模型经历较大的位移或旋转时，用户必须确保子模型也经历这些位移或旋转。使用基于节点的子建模时，驱动节点会自动考虑位移和旋转，以便子模型相对于全局坐标系正确定位。相反，对于基于曲面的子建模，仅使用曲面牵引力会使子模型不提供位移信息。相反，要考虑位移，子模型必须包括：应用的边界条件、从动节点和惯性浮雕。当同时使用这两种方法时，重要的是在所选区域保持一致的驱动方法，以防止因部分或过度驾驶定义而产生过度约束。
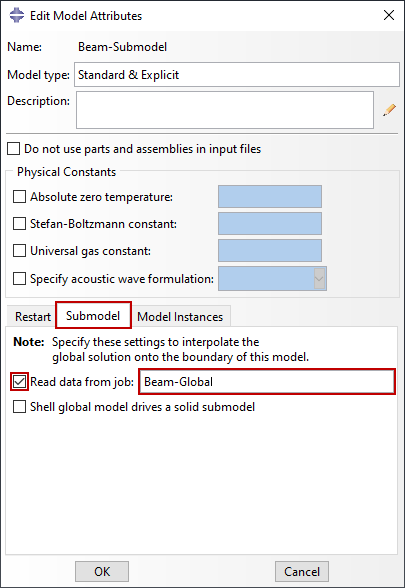
设置子模型时，应修改模型属性以引用输出数据库或结果文件。图 6 中显示的模型属性将导致 Abaqus 读取 Beam-Global.odb 输出数据库文件，并将这些结果用于分析Beam-Submodel.inp输入文件中定义的子模型。
子模型的局限性
此处将简要概述子模型方法的局限性，有关这些局限的详细信息可在文档中找到。
可在全局和子模型级别使用的单元仅限于一阶和二阶三角形和四边形连续体、壳或膜单元、一阶和二阶四面体、楔形或六面体连续单元。全局模型可以同时包含实体元素和壳元素，条件是所有从动节点都必须位于全局模型中的壳单元内。
子模型边界节点不能位于全局模型中信息不足的受驱动变量插值区域中。这包括只有一维单元（如梁、桁架、链接或轴对称壳）、用户单元、子结构、弹簧其他特殊元素或轴对称单元的区域。
使用壳单元时，通常应在全局级别避免每个节点壳单元（S4R5、S8R5 等）有五个自由度，因为不会保存旋转。这些图元不能用于壳到实体子建模。
子模型不能用于耦合热-电、耦合热-电化学和基于模式的线性动力学过程。基于曲面的子建模只能在一般静态过程中使用。
分析结果的验证
使用子模型方法，随后获得两组分析结果：第一组来自全局模型，给出行为的近似值，第二组来自精细的局部模型，提供更精确的详细输出表示。子模型过程中的一个重要步骤是验证结果。图 7 显示了基于节点的子模型的结果。在绘制应力梯度之前，首先检查模型在子模型区域中位移的一致性。如果发现位移存在重大差异，这将影响所有后续结果，应审查并重新提交模型。一旦发现位移匹配，就可以检查其他输出，例如应力。这里的改进是通过增加子模型区域中的网格密度来实现应力梯度。梁其他区域的应力可以从全局模型获得，在没有应力集中开口的情况下，粗网格就足够了。
