Abaqus-之线性粘弹性4

存储模量和损耗模量

为什么要关心循环加载响应？

• 在许多应用中，负载是循环的。

• 使用动态机械分析 （DMA） 设备可以轻松测量稳态循环响应。

• 我们可以根据动态数据（E'和E''）校准线性粘弹性模型。

  
  

  循环响应 - 完整解决方案

  在这个例子中，我将确定加载正弦应变历史的线性粘弹性材料的应力响应：

  ε（t）=ε0sin（ωt），我只考虑时间t≥0。在本系列的第 1 部分中，我展示了任何应变历史的应力都可以从以下公式获得：

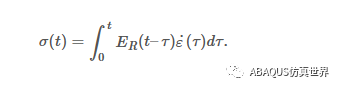                                       (1)

  
  

  将正弦应变历史插入该方程可得到：

  
  

               (2)

  根据变量替换重写积分：s=t–τ：

  
  

  

  
  

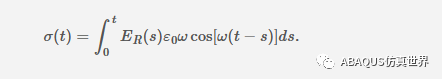
示例 - 完整解决方案

为了评估积分并计算实际应力响应，我们需要指定应力松弛模量。让我们假设以下 1 项 Prony 表达式：ER（t）=E0e−αt。将其插入公式（3）并计算积分得到：

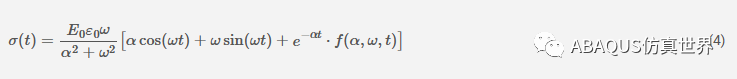
注1：我没有写出整个方程，在函数f（α，ω，t）中留下了一些项。

注2：在稳态下，部分应力与应变同相，部分应力与应变异相。

由正弦应变历史引起的预测应力-应变响应，在这种情况下，稳态响应在大约一个周期后达到。

图2.来自单项 Prony 序列模型的预测周期响应

循环响应 - 稳态

公式（3）给出了应力的完整瞬态解。如果我们只对稳态响应感兴趣，那么如果我们简单地将积分的上限更改为无穷大，我们仍然可以使用方程 （3）。此外，如果我们回想一下 cos（α−β）=cosαcosβ+sinαsinβ，则应力由下式给出：

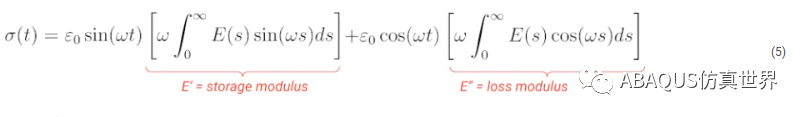
可以重写为：

Tan三角函数

从等式（6）我们知道应力是由sin和cos项给出的，也可以写成：

σ（t）=σ0sin（ωt+δ）

这个等式也可以写成：σ（t）=σ0sin（ωt）cosδ+σ0cos（ωt）sinδ。

这给了：

总结

• 存储模量（E'）和损耗模量（E''）通常使用DMA实验进行测量。

• Prony系列项可以从动态数据中确定。