LK-99的超导转变温度只有14.5K吗?!
近期热点
LK-99室温超导
NEWS
”
最近LK-99室温超导的报道引发了海啸般的狂潮,从业余材料爱好者到专业实验室,从开直播的到烧试瓶的,大家都想来碰碰运气,股票也跟着涨了几倍。虽然有人成功复 制了一些有排磁性质的碎片, 看似半飞起来,但也有人未能看到任何效果。因此,尽管合成这种材料的过程看似烤面包一样简单,但实际上要产生出一大块样品仍然非常不容易。
在这种情况下,对这种材料进行一些理论研究就十分有必要了。美国劳伦斯国家实验室的Griffin眼急手快,是第一个计算LK-99电子结构的人,她发现费米能量处有一个平带,并且发现它是一种铁磁材料。平带已被用来解释很多强关联的多体效应。然而,室温超导的强关联效应还只是一种猜测,并没有一个具体的理论。另外,这个平带很有一些诡异之处,时而出现,时而消失,它的原子来源与原子结构的关系都还没有具体被阐明。因此,对这种材料进行更仔细、更深入的计算就很有必要了。

今日话题
用PWmat以及相关模块来研究这个问题
作为吃瓜群众,我们对这一问题也充满好奇。看着着急,手痒痒,不如下场自己干。在这里,我们用PWmat以及相关模块来研究这个问题,并直接计算超导温度。在此也给大家汇报一下我们的结果。
平带的来源以及与原子结构的关系
我们先查看了一下网上发布的原子结构,使用了带有两个OH基团的CuPb9(PO4)6(OH)2,用spin=1 非自旋极化模式,先做原子弛豫,再进行电子能带计算,结果如图一所示。在费米能附近是有一个半填充的平带。如果用spin=2自旋极化模式, 主自旋一边就被完全占有了,而少自旋一边却完全没有被占有,成为一个磁性半导体。这一条能带来自于哪里呢?把它的波函数画出来,如图二所示,它是一个Cu原子的dxy态与旁边的四个O的p态相杂化的结果。

图一:CuPb9(PO4)6(OH)2能带,PWmat spin=1计算
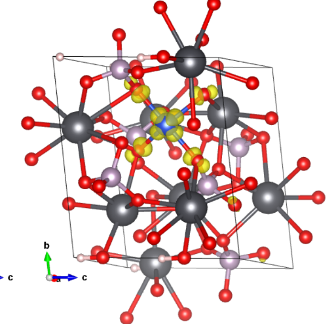
图二:平带的波函数(平方)图
虽然这看似不错,但仔细一想,不对呀!网上的能带在费米能级附近有两条带,我们的只有一条。我们又用了Griffin发布的原子结构,无论是用PWmat 还是 VASP计算,也都只有一个能级。这就怪了!事出无常必有妖,值得深究一下。
经过一番混乱挣扎,发现这个结构确实有一些奇怪的地方。首先,两个OH可被换成O,但这似乎并不影响结果。另外,两个O可被换成一个O,成为CuPb9(PO4)6O,它与CuPb9(PO4)6O2的比较显示在图三之中。除去失掉的一个氧原子,在CuPb9(PO4)6O中,通过原子弛豫,Cu原子更向下偏移,从而只有三CuO键,而在CuPb9(PO4)6O2中,Cu原子拥有四个CuO键。下面可以看到,正是这个价键的不同,造成了平带的不同。最后,经过对CuPb9(PO4)6O的结构弛豫,再计算它的能带结构,我们终于在费米面附近看到两个平带能级,哇啦!计算的能带图被显示在图四之中。我们在图二中看到CuPb9(PO4)6(OH)2(CuPb9(PO4)6O2的结果与之相似)平带能级来自于Cu的dxy态,那么CuPb9(PO4)6O中的另一条带来自于什么原子态呢?如图五所示,它来自于Cu的dz2态。正是因为CuPb9(PO4)6O2中Cu有四个CuO键,而CuPb9(PO4)6O中只有三个造成了这一区别。而这些又是因为远处失掉了一个O而造成的。所以总结起来说,CuPb9(PO4)6O有两条平带,而CuPb9(PO4)6O2只有一条,而OH或者O,没什么区别。

图三:两种可能结构的比较
红色球为O原子,黑色为Pb,粉红色为P,蓝色为Cu.绿色的圆环表示O失去的地方
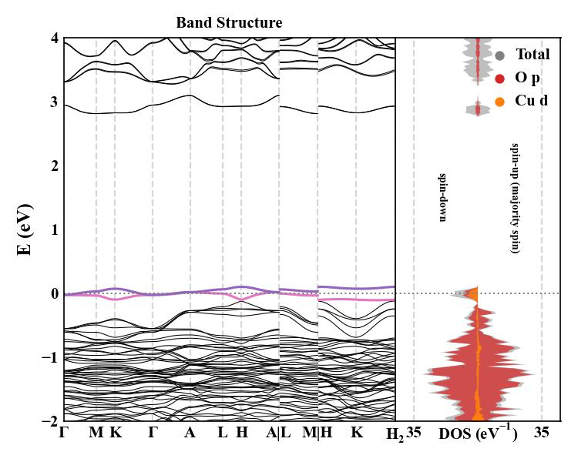
图四:PWmat计算的CuPb9(PO4)6O能带结构,spin=2
其中有两条平带能级。

图五:CuPb9(PO4)6O中的两条平带波函数的空间展示
(a),(b): 第一条平带,它与CuPb9(PO4)6O2中的平带相似;
(c),(d): 第二条平带,它有Cu dz2 结构。
预测超导转变温度
在知道了平带的来源之后,我们接下来尝试预测其超导转变温度。尽管对高Tc 超导的强相关效应进行了30多年的研究,但现在仍然没有一个很好的理论来解释基于铜氧化物的高温超导性。常规超导唯一成熟的理论是BCS理论。几个月前,热极一时的H基室温超导就是通过BCS理论进行预测的。因此一个有趣的问题是,基于BCS 理论,LK-99的转变温度Tc会是多少?然而,计算BCS理论Tc并不简单,它需要计算声子模式和电子-声子耦合常数。对于像LK-99这样的复杂材料来说,这是相当麻烦的。庆幸的是,龙讯旷腾有70多个不同的计算模块,专门用于计算材料的各种性质。这里面也包括计算金属体系的超导体Tc的模块Module-72。所以,是骡子是马,拉出来试试。
从上面研究可以看到,电子能带结构与原子结构密切相关。我们决定使用带有两个OH基团的 CuPb9(PO4)6(OH)2结构。不过在spin=2 的磁性体系计算中,该体系是一个磁性半导体。至少根据 BCS理论,磁性半导体显然不能成为超导体。事实上,普通超导体不可能具有磁性,因为磁性会破坏超导特性。但磁性相和非磁性相之间的能量相差很小,因此,为了计算超导体的Tc,我们采用了它的非磁性相,也就是使用了PWmat中的spin=1计算。如果人们非要用spin=2来计算,并且采用有两个平带的体系,我们估计得到的结果也会差不多。在这种设置下,费米能附近只有一个能带,而这一能带被部分占据,从而得到一个金属系统。这种平带体系,会使能带在费米能附近具有一个较高的状态密度,根据BCS理论,这是高Tc的有利条件,这让我们充满希望。
使用PWmat对该结构进行结构优化,随即我们利用Module-4:PyPWmat来计算了该系统的声子谱。值得一提的是在ω=113 THz 附近有两个非常高的声子模。这两个模式是氢氧价键伸缩模式。如果这是氢超导体,这种模式将是超导性的重要贡献者。但就目前的情况而言,它们对费米能附近的平带电子态的电声耦合没有太大贡献。因此,这两种模式并不重要,也就是说有或没有H都不会对Tc产生太大影响。
接下来我们计算电子声子耦合常数。为此,我们使用龙讯旷腾Module-62 EPC。在这个过程里我们利用Wannier 函数来计算电子-声子相互作用,从而插值得到更多的声子q点和电子k点。我们使用具有352个原子的2x2x2超晶胞,分别对每个原胞原子的位置做一个扰动来计算完整的电声耦合常数。得到电声耦合常数gjkn,k+qm后,可以继续用它进行后面费米能周围电子的电子-声子相互作用的计算,这个我们会用到龙讯旷腾Module-72。计算这个的目的是为了得到 ϒqj,这是由于费米面周围电子的电子散射而导致的声子寿命(展宽)。它代表声子对超导性的贡献。

当我们获得不同声子模式j和倒格矢q的ϒqj 后,我们可以代入以下方程来计算电子声子耦合(EPC)谱 。

这里N(εF) 是费米能级下的电子态密度,W(q)是由于使用对称性来减少q点而产生的声子权重,q是声子模式的倒格矢,并且j是声子模的指数,α是精细结构因子。计算出的F(ω)如图六(upper panel)所示,它可以与图六中的声子态密度进行比较。为进一步看到不同声子模对EPC的贡献,我们在图七中把不同声子模在Cu原子,以及与它拥有价键的四个O原子的振幅乘到DOS中,得到一个声子的Partial DOS。我们可以看到Cu和与之相连的四个O对于电声耦合的贡献集中在低频波段,电声耦合强度较大的频率区间15-17,26-30 THZ内O有很大的贡献,而0-10 THZ由Cu和O共同贡献。
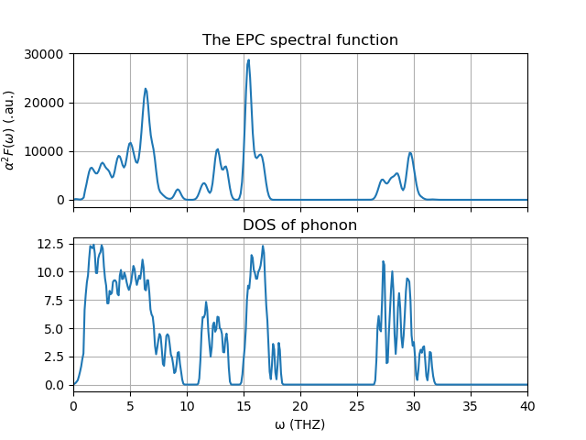
图六:声子态密度(bottom panel)与EPC谱 (upper panel)
注意,在上图DOS 中,有一个在ω=113 THZ 处的细峰没有被标出。此峰在下图EPC中并不存在
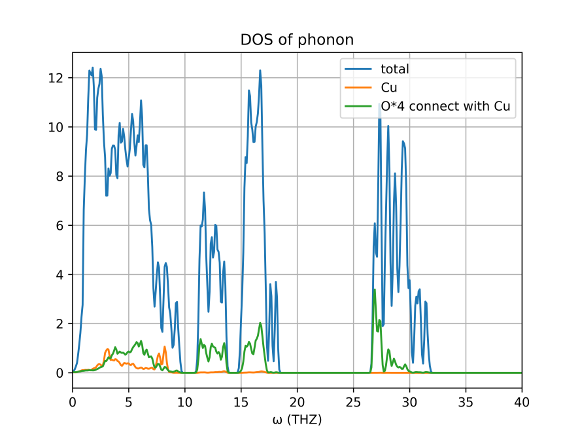
图七:声子分态密度
最后,为了计算超导转变温度,我们首先需要计算由电声耦合谱加权的对数平均声子频率。形式如下:
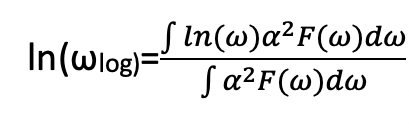
计算出的ωlog为8.86 THz,对应于67.63 K的温度。然而BCS的超导转变温度(Tc)不是 ωlog,而是有一个附加因子exp(-(1.04(1+λ)/(λ-μ*(1+0.62λ))。λ代表总体电子-声子耦合强度也由 F(ω)计算得出:

我们计算出的λ为2.97,这代表了强耦合状态。该强耦合状态下的最终Tc度预测的形式为:
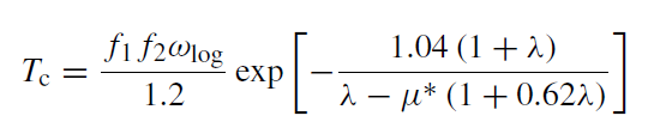
其中f1和f2是两个额外的微调因子,也取决于λ。在我们的例子中,f1=1.25,f2=1.007,μ*=0.13。因此,最终我们计算出的BCS的Tc为14.5K!呜呼哀哉,这温度很低呀,离室温超导相距甚远!
14.5K要远低于实验预测的室温Tc。尽管如此,我们并不能以此完全排除LK-99成为室温超导体的可能性。它可以排除的是使用BCS机制成为室温超导的可能性。因此,如果这确实是室温超导性,那么它一定来自于某种新颖的机制。请注意,之前提到的作为λ的函数的附加指数因子exp(-(1.04(1+λ)/(λ-0.13*(1+0.62λ))如下所示:

图八:λ 的函数的附加指数因子
因此,无论λ有多大,该因子的最大值约为0.3。校正因子f1和f2仅略大于1。因此,根据BCS理论,为了具有高Tc,ωlog必须非常大。换句话说,对于接近费米能量的电子态,某些高频(轻原子和强键)必须对电子-声子耦合有很高的贡献。这仅适用于与H相关的振动(其ω对应的Tc大约为900K,但乘上指数因子后,Tc为270K)。如想要进一步提高这个温度,可以通过高压来增加键的强度,从而提升声子的频率,也让费米面附近的电子在氢原子上有更大的波函数振幅。这就是为什么在H基的高温超导中,往往伴随着高压的出现。
第一性原理计算的作用
最后,通过这一练习我们可以看到,使用第一性原理计算来研究什么是费米表面电子态,以及与H相关的高频声子模式是否会与这些费米表面电子态耦合是非常有用的。希望上面的计算给大家提供了一些有关这个材料的启发。到底会不会有其他的机制导致了室温超导,我们拭目以待。我们也欢迎大家来使用龙讯旷腾自主开发的Module来计算材料的各种性质,包括超导转变温度(上文提到的所有Module模块我们列在了下方链接里)。希望有一天,高温超导终将实现。
70余个Module的下载地址
http://www.pwmat.com/module-download
Module-72使用教程
http://modulefiles.pwmat.com/pwmat-resource/module-download7/pdf/EPC_spectral_function.pdf
Module-4使用教程
http://modulefiles.pwmat.com/pwmat-resource/module-download7/pdf/guide_PyPWmat.pdf
Module-62使用教程
http://modulefiles.pwmat.com/pwmat-resource/module-download7/pdf/guide_EPC.pdf
网址
”
—E N D—
公司简介
北京龙讯旷腾科技有限公司是成立于2015年的国家高新技术企业,是国内材料计算模拟工具软件研发创新的领导者,致力于开发满足“工业4.0”所需的原子精度材料研发Q-CAD(quantum-computer aided design)软件。公司自主开发的量子材料计算软件PWmat(平面波赝势方法并基于GPU加速)可以进行电子结构计算和从头算分子动力学模拟,适用于晶体、缺陷体系、半导体体系、金属体系、纳米体系、量子点、团簇和分子体系等。




