通信的调制技术

导读：射频技术服务于现代通信与电子战，但是射频只是一个载体，真正有用的“信息”是基带信号，信号的传输类型对整个射频方案的设计起着决定性的作用。

在设计射频方案时，射频工程师都会发出灵魂一问“恒包络还是非恒包络？非恒包络峰均比几？”

今天就来说一下这些恒包络调制和非恒包络调制。

一、恒包络

设一个符号为g(t)*cos(ω₀t+φ)，g(t)为矩形开关选通脉冲[频域为G(jω)]，非线性用3次函数逼近Vo=aVi+bVi2+cVi3，则

Vo=a* g(t)*cos(ω₀t+φ)+b* g2(t) *cos²(ω₀t+φ)+c*g3(t) *cos³(ω₀t+φ);

cos³(ω₀t+φ)=cos(ω₀t+φ)*cos²(ω₀t+φ)=1/2*cos(ω₀t+φ)*[cos(2ω₀t+2φ)+1]

=1/4*cos(3ω₀t+3φ)+3/4*cos(ω₀t+φ)

Vo=a*g(t)*cos(ω₀t+φ)+b* g²(t) *cos²(ω₀t+φ)+c/4*g³(t)* cos(3ω₀t+3φ)+3c/4*g³(t)* cos(ω₀t+φ)

输出的基频为Vo=(a+3c/4)* g(t)*cos(ω₀t+φ)

∵g³(t) =g(t)

所以恒包络基本上没有三阶互调问题。

但矩形脉冲g(t)的频谱（sinc函数）副瓣太高，会泄漏到邻道。

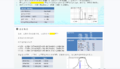
从时域上来看，幅度不变化的，就是恒包络调制。所以FSK，GMSK,MSK，OQPSK都是恒包络调制。

这里要特别说一下QPSK，从星座图上来看，QPSK的幅度都是相同的，但是为什么QPSK不是恒包络？

从立体图上看，QPSK是一个调幅调相的信号，虽然幅度都是恒定的，但是相位有变化00,01，10,11，从01到10需要经过零点，经过原点的某瞬及幅度就为0了（实际上是非常小），这样的话整个信号峰均比就会变大，所以QPSK是非恒包络。

二、非恒包络

设一个符号为g(t)*cos(ω₀t+φ)，g(t)为滚降包络开关脉冲，由于非线性，用3次函数逼近Vo=aVi+bVi2+cVi3，则

Vo=a* g(t)*cos(ω₀t+φ)+b* g2(t) *cos2(ω₀t+φ)+c*g3(t) *cos3(ω₀t+φ);

Vo=a*g(t)*cos(ω₀t+φ)+b* g2(t) *cos2(ω₀t+φ)+c/4*g3(t)*cos(3ω₀t+3φ) +3c/4*g3(t)* cos(ω₀t+φ)

输出的基频为Vo= [a*g(t)+3c/4*g3(t)]*cos(ωt+φ)

x(t)*y(t)←→1/(2π)*X(jω)ÄY(jω)，f(t)Äd(t)=f(t)

cos(ω0t+φ) ←→π[d(ω-ω0) *ejφ+d(ω+ω0) *e-jφ] ，

3c/4g3(t)*cos(ω₀t+φ)←→3c/8*ejφ*G3(jω-ω0)+3c/8*e-jφ*G3(jω+ω)

非线性增加了一项基频3c/4g3(t)*cos(ω₀t+φ) ，但有别于信号频谱，包络不同。

滚降包络因子g3(t)的频谱;

g3(t)= g(t)* g(t)* g(t)

g3(t) ←→1/(2π)*G(jω)*[1/(2π) G(jω)*G(jω)]

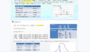
还是以QPSK为例，可以看到QPSK的幅度在变化。

讲了这么多，问题的关键是：射频工程师为什么要分析调制包络？？

因为在实际中，我们经过了调制之后的信号，因为比较微弱，还需要经过功放（功率放大器）的放大才发射出去。

恒包络调制因为信号幅度完全相同，不会产生三阶互调，所以对射频的设计没有线性要求，方案设计上简单很多。

非恒包络调制为了使得信号在经过放大之后不失真，我们需要使用线性功放。但是线性并不能无限回退，我们需要在以最低成本、最低功耗设计指标。所以根据包络信号的峰均比、EVM我们可以选择合适的线性器件。

结语：射频设计的最重要思想就是线性，而制约线性设计的最重要因素就是信号的包络方式，虽然调制方式不归射频工程师，但是对常见的调制方式的优劣势有所了解，对成为一个系统工程师还是有一些帮助的。