十九、流体力学理论-高斯公式
这次我们谈谈流体力学理论知识-高斯公式,对雷诺输运定理及流体力学三大守恒方程比较熟悉的同学,会发现这些方程在推导的过程中经常会出现高斯公式,当然还会出现咱们文章十二中讲到的散度和梯度,这些都是流体力学基础中的基础。
1.高斯公式的各种形式
先直接给出高斯公式:设空间有界闭合区域Ω ,其边界∂Ω 为分片光滑闭曲面。函数P,Q,R及其一阶偏导数在Ω上连续,那么:

仔细观察上式,会发现等式左端可以应用文章十二讲到的散度公式,对于等式右端cosα*dS即为微元面积S在yz平面上的投影,同理cosβ*dS即为微元面积S在zx平面上的投影,cosγ*dS即为微元面积S在xy平面上的投影,将上式可以进行变形得到:

如果我们将上式中的物理量用速度替换会更加容易理解,

其中V表示速度矢量,u、v、w表示三个方向上的速度分量。
注:高斯公式只对矢量物理量适用,因为只有矢量才有散度之说(文章十二内容)
2.散度的物理意义
从公式3能看到什么呢?首先我们回顾一下散度的物理意义,散度用于表征空间各点矢量场发散的强弱程度,散度的意义是场的有源性。我们用下图表示,六面体内有一点A可以往外流出流体。

我们以dV为微元研究对象,等式左端

是一个体积分,表示的实际上是微元体内总体积流量的变化量。
由于流体可变形,因此上式可理解为单位时间内变形后的体积-变形前的体积=体积变化量,传热学书本上对此有详细推导,我们简单推导一下,ux,vy,wz分别表示速度在x,y,z方向的分量,ux+dx,vy+dy,wz+dz分别表示速度在x+dx,y+dy,z+dz方向的分量,则:

微元体在x处的流体体积流量:
x方向体积流量为:

y方向体积流量为:

z方向体积流量为:

总体积流量为:

微元体在x+dx处的流体体积流量:
x方向体积流量为:

y方向体积流量为:

z方向体积流量为:

总体积流量为:

总体积流量相减得到微元体内体积净增量如下,就等于等式左端
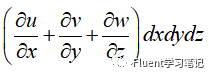
因此如何理解散度呢?可以认为散度是流场中的一个喷泉,当散度为正时,喷泉向外喷水,当散度为负时,喷泉向里吸水,散度为0,表示喷泉不喷不吸。而等式左端积分就表示在整个流场中单位时间内喷泉喷出或吸收了多少水量。所以说,散度的意义是场的有源性。
3.高斯公式的理解
我们已经知道了高斯公式等式左端就是体积流量的变化,等式右端是什么呢?

等式右端更加容易理解,我们能看出来等式右端实际上一个面积分,udydz用x方向的速度乘以x方向的截面,显然表示的是x方向的体积流量,同理vdzdx表示y方向的体积流量,wdxdy表示z方向的体积流量。将三者相加,表示的是整个从封闭曲面流进或流出的流体体积流量。这也是为什么定义里强调了闭合区域的原因。
等式左端表示的是整个流场体积的变化,等式右端表示的是从流场边界流进或流出的流体体积(为便于理解,省略流量二字),两边是否相等呢?
显然相等,从流场边界流进或流出的体积量必然会在流场中体现出来,即等于流场中多出来或减少掉的体积量。
因此高斯公式实际上就是将体积分与面积分联系了起来,
它告诉我们流场中失量物理量的改变必然会通过流场边界表现出来,
内部的改变必然会在外部有所体现,
人内里的气质必然会表现在言行上(升华了)




