用UDS求解换热方程(第一类边界条件,附代码)
1 引言
本案例将详细讲解如何用UDS求解换热问题,当然了,FLUENT打开能量模型自然就可以求解换热问题了。另外,本案例讨论的换热问题为非流固耦合换热,即计算域只有流体。本案例的宗旨在于进一步学习UDS求解变量的方法。
FLUENT UDS通用方程如下:
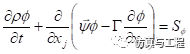 (默认
(默认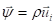 ) (1-1)
) (1-1)
对流换热能量守恒方程如下:
 (1-2)
(1-2)
边界条件:
恒温边界(第一类边界条件): 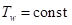 (1-3)
(1-3)
恒热流密度边界(第二类边界条件):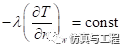 ( 1-4)
( 1-4)
对流换热边界(第三类边界条件): 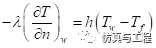 (1-5)
(1-5)
2 问题分析
分别对纯导热问题和对流换热问题进行计算,边界条件取第一类。
2.1 纯导热问题
以不可压缩二维稳态无源纯导热问题为例,如图1所示,一个1×0.1m2的方形平面空间,上下面以及左边为恒温壁面(21℃),右边温度60℃。为方便问题分析,内部介质的导热系数取1W/m℃,此时只需要在Equations中关闭流动相关方程即可。不可压缩二维稳态无源纯导热方程如式2-1,与通用UDS方程对比可知,没有时间项,没有对流项,没有源项,扩散系数为 。对于湍流流动,扩散系数不是这个。对于第一类边界条件问题,扩散系数可以为1,即导热方程进行约分简化,也就是说,对于所有边界温度都已知的情况,导热系数对于温度分布没有影响)。因此,只需要在材料中设置扩散系数为1即可。
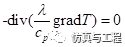 (2-1)
(2-1)

图1 问题描述
采用FLUENT软件自带能量方程及边界条件直接进行计算,温度结果如图2所示,采用UDS计算的温度结果如图3所示(边界条件为第一类,用Specified Value),可以看出,计算结果几乎完全一样。

图2 FLUENT软件自带能量方程及边界条件计算结果

图3 UDS计算结果
中心温度分布线
2.2 对流换热问题
同样采用以上的计算域,考虑对流换热。不可压缩二维稳态无源对流换热方程如式2-2,与通用UDS方程对比可知,没有时间项,没有源项,扩散系数为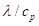 (UDF编写),对流项为标准质量流率,也可以用DEFINE_UDS_FLUX函数自定义(代码见附录)
(UDF编写),对流项为标准质量流率,也可以用DEFINE_UDS_FLUX函数自定义(代码见附录)
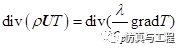 (2-2)
(2-2)
采用标准k-e模型。
边界条件:入口速度2m/s,温度60℃,UDS值60(Specified Value);
上下壁面:wall,温度21摄氏度,UDS值21(Specified Value);
出口:outflow,UDS值0(Specified Flux);(假定流动充分发展,流动方向上的梯度为0,详见数值传热学P232)
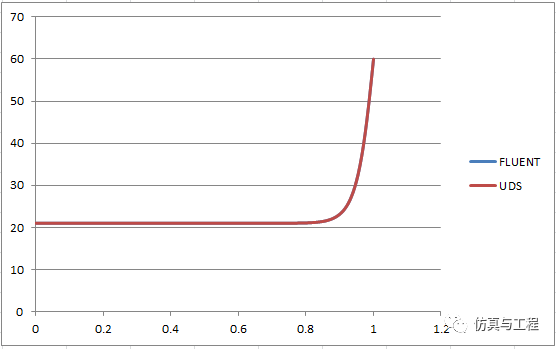
采用FLUENT软件自带边界条件直接进行计算,结果如图4所示,采用UDS计算的温度结果如图5所示。中心区域的温度分布线如图6。可以看出,温度分布几乎一致,但从中心线温度分布线看,两者存在一定误差,特别是越靠近出口,误差越大。笔者认为这是因为采用标准k-e湍流模型,而UDS的扩散系数是对NS方程而言的,湍流流动的扩散系数与NS方程下的扩散系数不一样。
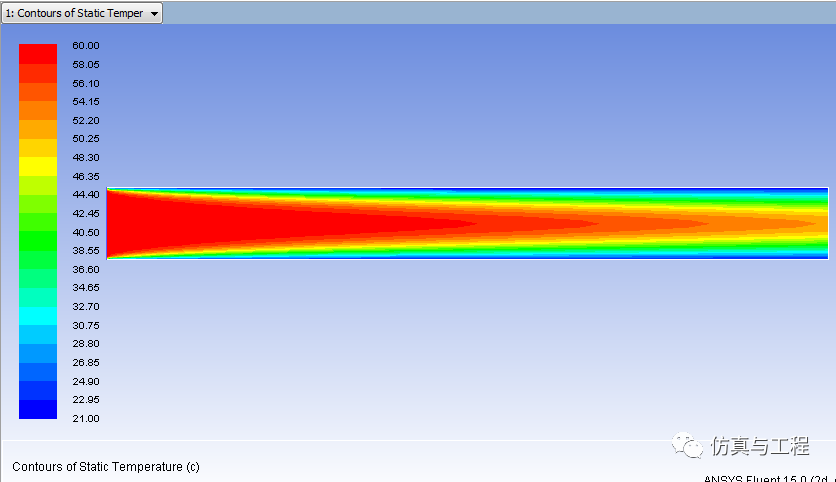
图4 FLUENT软件自带能量方程及边界条件计算结果

图5 UDS计算结果

图6 中心区域温度分布对比
参考文献:
[1]FLUENT帮助文档
[2]杨世铭,陶文铨.传热学(第4版)[M].北京:高等教育出版社
[3]陶文铨.数值传热学[M].西安:西安交通大学出版社
附录 UDF代码
DEFINE_UDS_FLUX(MyFlux,f,t,i){return F_FLUX(f,t);}DEFINE_DIFFUSIVITY(MyDiff,c,t,i){double lamda=C_K_L(c,t); //获取导热系数double cp=C_CP(c,t); //获取比热return lamda/cp;}




