FLUENT圆管层流压降计算
正文共: 1194字 12图 预计阅读时间: 3分钟
1 前言
在充分发展的定常层流流动中,圆管内的速度分布满足以下旋转抛物面关系:
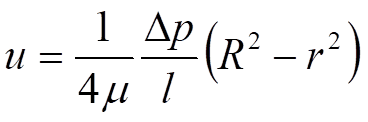
圆管轴线上的速度最大,为:

圆管截面上的平均速度为:
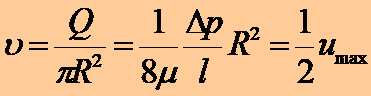
在圆管充分发展的定常层流中,单位重量流体的压损和平均速度的关系为:

沿程损失系数可表示为:
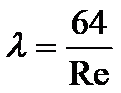
以上是圆管充分发展定常层流的基本公式,可用来计算流动阻力。今天我们用FLUENT做一个计算案例,同时与理论公式计算结果进行对比。
2 案例描述
一根长1m,内径20mm的光滑圆管,介质为水,密度998.2kg/m3,粘度0.001Pa·s,平均流速0.1m/s,求流动压损。
3 理论公式求解
根据已知条件,雷诺数为:
Re=ρud/μ=998.2×0.1×0.02/0.001=1996.4
则沿程阻力系数为:
λ=64/Re=0.032058
于是阻力损失为:
ΔP=ρλ(L/d)u2/2=998.2×0.032058×(1/0.02)×0.12/2=8Pa
4 FLUENT求解
4.1 建模与网格
根据已知条件建立二维轴对称模型,并划分六面体网格,对壁面附近网格进行适当细化,节点总数10500。

4.2 求解设置
根据已知条件设定水的物性,入口为速度边界,出口为压力边界,表压为0Pa,其余设置保持默认即可。这里为了对比充分发展和非充分发展段的区别,我们分别计算了入口速度为平均速度均匀分布以及入口速度为充分发展分布两种情况,其中对于充分发展分布,根据已知条件编写以下UDF速度边界。
DEFINE_PROFILE(inlet_x_velocity, thread, index){real x[ND_ND];real y;face_t f;begin_f_loop(f,thread){F_CENTROID(x,f,thread);y=x[1];F_PROFILE(f,thread,index)=2000*(0.01*0.01-y*y);}end_f_loop(f,thread)}
4.3 计算结果
首先,我们看一下入口速度为0.1m/s的压力损失,为13.68Pa,显著大于理论公式计算值8Pa。我们观察一下入口位置及附近的速度分布,可以看到入口下游一段距离的边界层逐渐增厚,入口的边界条件有点类似于突然缩小的局部阻力件,因此这种情况计算的压损会更大。


此时的进出口速度分布曲线如下,入口为非充分发展状态。

其次,我们看一下入口速度为充分发展分布的情况,压力损失为7.995Pa,与理论公式计算结果一致。我们观察一下入口位置及附近的速度分布,可以看出流动方向上分布均匀,边界层厚度一致。


此时的进出口速度分布曲线如下,两者分布一致,说明整段管为充分发展状态。
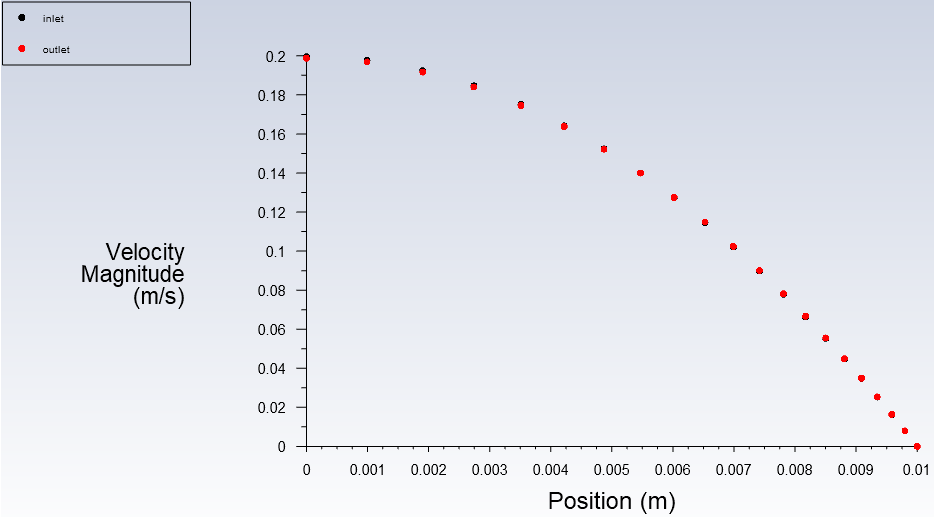
5 总结
沿程阻力损失的理论公式适用的是充分发展流动状态,在进行CFD计算时需要注意流动边界条件设置的合理性,否则压力损失计算会不准确。




