一个管道气液两相流模拟

1年前浏览506

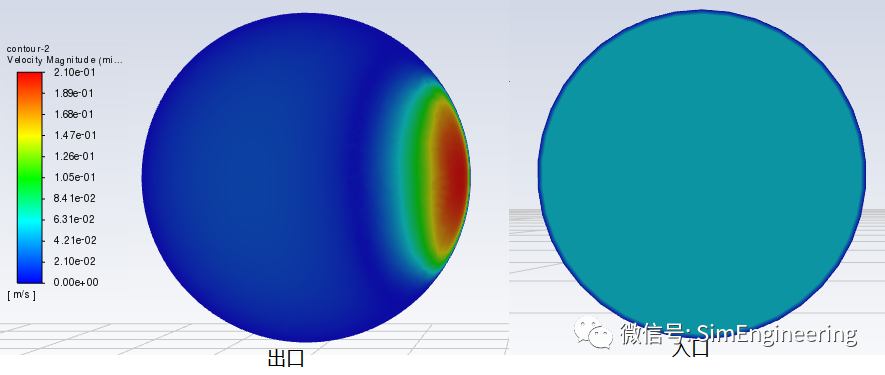
正文共： 868字 12图预计阅读时间： 2分钟

1 前言

本案例来自如下的工程应用，一段管道的走向分为竖直向上和水平，液态水从底部向上流入，最终从水平出口流出，要计算出口的液位高度。

2 网格与求解设置

竖直向上的管道肯定是满管流，而水平管是满管流还是非满管流取决于水流量，本案例的水流速度按经验判断很小，因此应该是非满管流，即水平管是气液两相流。为了捕捉液面，我们采用VOF模型，划分网格时尽可能采用细致的网格。我们划分多面体网格，节点数2722484，最小正交质量0.22，暂未追求高质量网格。

我们根据水流量计算入口的雷诺数约为340，按层流考虑更为合适，因此采用层流模型。

采用VOF两相流模型，主相为空气，次相为液态水。

入口采用速度入口边界，全部为液态水。

出口采用压力出口，表压为0Pa，回流全部为空气，表示外部为大气环境。

创建一个监视器，监测出口的液体水流量，当出口的流量和入口流量相等时，达到稳态。

瞬态求解，时间步长0.001~0.004s之间。

3 计算结果

我们看一下出口的液态水流量，最终和入口基本达到一致，认为达到了稳态。

我们看一下液面在管道内的分布，水在进入水平管后转变为非满管流，形成气液两相流，管道上部为空气。

出口面的液位分布如下，液面高度的获取可以有多种方法，比如从中心底部向上划一条线，根据这条线上的液体体积分数来获得高度坐标；也可以将这个面的体积分数云图和坐标点数据导出到后处理软件，再进行液体高度坐标提取；还可以根据出口的面积加权体积分数乘以出口面积得到液态水流截面的面积，再根据弓形面积计算公式间接获得高度。