Ansys Workbench工程应用之——结构非线性(中):材料非线性(4)粘弹篇
上三篇文章详细介绍了Ansys Workbench中的塑性和超弹性,本文讨论Workbench中用于模拟非晶态聚合物、玻璃等材料的粘弹性本构,图惜大概搜索了下,目前好像还没有人写Ansys Workbench的粘弹性,原本计划用1周时间写完,但是写作过程中发现知识储备太少,于是又花了3周恶补了一番高分子物理,薅飞了不少的头发,终于勉强能写一些肤浅的知识,作为抛砖引玉的引子。

4 粘弹性
4.1.1 聚合物材料基础
一般把相对分子质量高于10000的分子称为高分子。由于高分子多是由小分子通过聚合反应而制得的,因此也常被称为聚合物,在工程材料上被称为塑料和橡胶。如聚乙烯、聚丙烯、聚氯乙烯、聚甲醛、聚氨酯等等。
凝聚态为物质的物理状态,是根据物质的分子的聚集状态来区分的,通常包括固体、液体和气体。高分子聚合物一般不存在气体状态。
相态为物质的热力学状态,是根据物质的结构特征和热力学性质来区别的,包括晶态相、液态相和气态相。一般情况下,固体就是晶态相,但也有例外,例如,玻璃不能流动,具有一定的形状,属于固体,但从结构上来讲却属于液态相(非晶态固体)。除了上述物质三态之外, “液晶”具有流动性,从物理状态而言为液体,但其结构上保存着晶体的一维或二维有序排列,属于兼有部分晶体和液体性质的过渡或中介状态——液晶态。

非晶态聚合物是指完全不结晶的聚合物(类似于玻璃),如有机玻璃PMMA,聚碳酸酯PC,生物组织等、以及其他无规聚合物等。相反,晶态聚合物是指在一定条件下能全部或者部分结晶的聚合物,如聚乙烯、聚乙炔、聚甲醛、聚四氟乙烯、尼龙等,以及等规和间规聚合物等。通常,非晶态聚合物呈现透明状,半结晶的晶体聚合物呈乳白状,结晶度越高越不透明,当然也有例外。
名词解释——聚合物的分子构型:
除了聚乙烯PE(分子式-CH2-CH2-)、聚乙炔PA(分子式-CH=CH-)等少数聚合物外,大部分聚合物的分子式含有非对称的取代基。当高分子聚合时所有的取代基都在同一侧称为等规聚合物,当取代基有规律地间隔分布于两侧称为间规聚合物,当取代基分布无规律时称为无规聚合物。下图以PVC为例。

4.1.2 粘弹性的概念
如果材料具有弹性部分和粘性部分,则称该材料具有粘弹性。粘弹性是率相关行为,它的响应可以看作是弹性与粘性的组合。在施加载荷时,弹性变形是瞬时的(与速率无关的)、在变形过程中储存能量的、变形可恢复的部分;而粘性是会随着时间的推移而发生(与速率相关的)、在变形过程中耗散能量的部分。

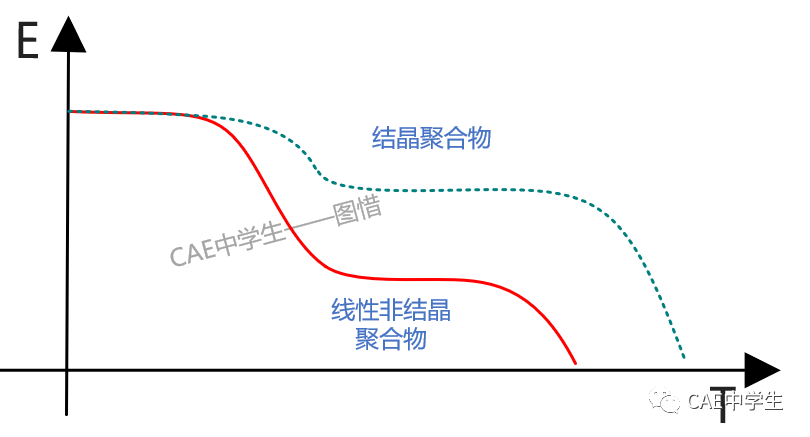
粘弹性模型通常描述非晶态聚合物的变形行为,它们的行为随温度而改变,如下图,E表示材料的模量,即应变/应力,是材料抵抗变形能力的大小,模量越大,表示材料刚度越大。Tg为玻璃转变温度,Tf为熔点。交联聚合物,特别是高度交联的聚合物不会熔融,所有没有流动区。

在玻璃态区,材料响应与玻璃(非晶态固体)类似,粘性很小可以忽略。在线性聚合物的流动区,材料响应与粘性液体类似,弹性很小可以忽略。在玻璃转变温度附近20~30℃范围,模量下降了近1000倍,聚合物的行为与皮革相似,同时具备弹性与粘性。Tg通常取作模量下降速度最大处的温度。在橡胶弹性平台区,聚合物处于高弹态,材料响应与某些橡胶类似,同时具备弹性与粘性。粘弹性模型关心的便是聚合物在玻璃转变区与橡胶弹性平台区的力学响应。
那么晶体聚合物呢?对于理想的100%的晶体,不存在玻璃转变温度,温度变化时只在晶相固体与液体之间转换。但是对于聚合物,没有理想的100%晶体状态,通常结晶聚合物是部分结晶的或半结晶的多晶体,既有结晶部分,又有非晶部分。
因为结晶聚合物中含有非结晶部分,因此仍有玻璃化温度,但是由于微晶的存在,使非晶部分链段的活动能力受到牵制,一般结晶聚合物的Tg要高于非晶态同种聚合物的Tg。例如:PET,对于无晶PET的Tg=69℃,而结晶PET的Tg=81℃(结晶度=50%),随结晶度的增加Tg也增加。可见,晶态聚合物由于结晶度的不确定性,粘弹性的研究更复杂,所有一般只研究非晶体(完全不能结晶或结晶度很小的)聚合物的粘弹性。
名词解释——聚合物的分子构造:
通常情况下,合成高分子多为线性,也有高分子呈支化或交联结构。
线性聚合物又称热塑性聚合物。由于其分子链结构规则易结晶,所以结晶度、密度、熔点和、强度都比支化聚合物高。线性大分子在一定溶剂下可溶解,在一定温度下可熔化,即可溶可熔。
支化聚合物与线形聚合物的化学性质相似(易溶易熔),但物理机械性能不同,支化破坏了分子的规整性,故结晶度大大降低。本文所述的线性聚合物包括了支化聚合物。
交联聚合物也称热固性聚合物,由线性聚合物或低分子聚合物通过化学反应得到的三维空间交联的体型网状结构。交联聚合物不溶不熔,轻度交联聚合物尚能部分结晶,高度交联聚合物则完全失去结晶能力。热固性塑料酚醛、环氧、不饱和聚酯,硫化橡胶,交联聚乙烯等均为交联高分子聚合物。
以聚乙烯为例,不同分子链结构的性能如下表

4.1.3 粘弹性材料的特性
粘弹性材料静态特征表现为蠕变、应力松弛;动态特征表现为滞后和内耗。
蠕变是指在一定的温度和较小的恒定应力作用下,材料的应变随时间的增加而增大的现象。蠕变大小反映了材料尺寸的稳定性和长期负载能力。例如,软质PVC丝勾着一定质量的础码,就会慢慢地伸长,解下础码后,丝会慢慢地回缩,这就是软质PVC丝的蠕变和回复现象。
对于粘弹性材料,卸载后会随时间发生部分或全部弹性恢复。
聚合物在温度升高到Tg温度附近开始具有粘弹性。比如PIB(聚异丁烯)Tg=-71°C,PU(聚氨酯)Tg=-35°C,天然橡胶Tg=-73°C,它们在室温时便处于高弹态表现出粘弹性,而PS(聚苯乙烯)Tg=100°C,POLY(聚甲基丙烯酸乙酯)Tg=62°C,它们在室温时处于玻璃态表现出弹性。
金属材料在高温下具有显著的粘性(相对于熔点)。不可恢复的蠕变为粘塑性,可恢复的蠕变为粘弹性。
除此之外,玻璃、土壤、生物组织和纺织品等多种材料在一定温度区间表现出粘弹性行为。

应力松弛表现为对于恒定的应变,粘弹性材料随着时间的推移表现出应力减小的现象。

粘性流体,如粘流态的聚合物和未硫化的弹性体,应力会松弛到零,当施加的应变释放时,不会恢复。
粘弹性固体,如高弹态的聚合物和硫化弹性体,应力将逐渐放松到非零应力水平。在释放施加的应变后,弹性部分将立即恢复,粘性部分将随着时间的推移完全恢复。
滞后和内耗:粘弹性材料具有粘滞因子,它们具有随时间变化的应变速率。纯弹性材料加载和卸载过程不耗散能量(热),然而,粘弹性物质加载和卸载过程中或消耗能量。快速重复加载或导致粘弹性材料产生热量,反复拉橡皮筋发热就是这种原理。跑鞋或包装材料,在缓冲冲击的应用中使用粘弹性材料的主要原因之一是它的能量耗散能力。

4.1.4 粘弹性的表示模型
为了更形象地表示粘弹性行为,前人总结出如下表示方法:
弹性符合胡克定律,通常用一个弹簧表示,弹簧的刚度即为杨氏模量E,应力为杨氏模量与应变之积,即弹簧刚度一定情况下,拉动弹簧的力越大,弹簧伸长越多。

粘性采用粘壶阻尼器表示,有外力作用时活塞才会移动,外力卸载后活塞将处于悬停状态。粘壶中液体的粘度为η,应力为粘度与应变速率之积,即粘度一定情况下,拉动活塞的力越大,活塞运动速度越快。

下面就开始简单地组合这个弹簧和这个阻尼器。
首先将弹簧和阻尼器串联在一起,便形成了Maxwell(麦克斯韦)模型。

Maxwell模型的蠕变与应力松弛行为如下图,可见Maxwell模型并不能正确模拟蠕变,能模拟线性非晶态聚合物应力松弛行为。
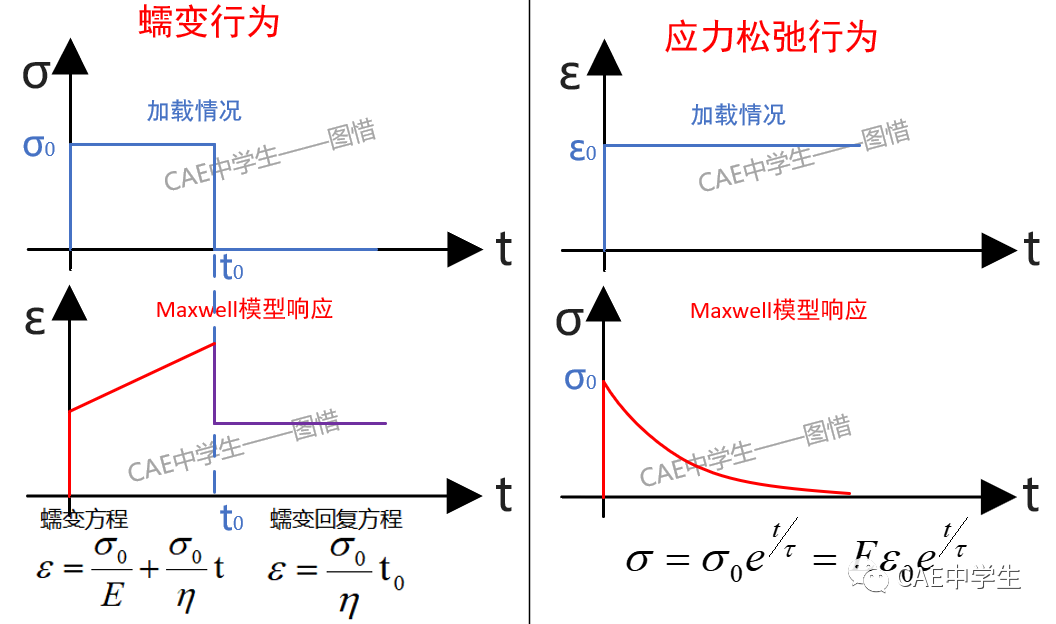
上图公式中τ为松弛时间:τ=η/E
松驰时间在麦克斯韦模型中的宏观意义为应力降低到起始应力σ(0)的1/e倍(0.368倍)时所需的时间,即松弛过程完成63.2%所需时间。
既然串联不理想,那么我们就将弹簧与阻尼器并联,便形成了Kelvin-Voigt(开尔文)模型。

Kelvin-Voigt模型的蠕变与应力松弛行为如下图,可见Kelvin-Voigt模型在并不能正确模拟应力松弛,但是基本上可用来模拟交联聚合物的蠕变行为,这里所谓基本,是因为未能反映出加载起始和卸载起始的弹形变部分。

上图公式中松驰时间τ=η/E,在开尔文模型中的宏观意义为蠕变过程完成63.2%所需时间,有别于麦克斯韦模型,此处松弛时间又称为推迟时间。
既然串并联都不理想,那么我们就再捣鼓捣鼓,将一个弹簧和一个Maxwell模型相并联,便形成了标准线性模型(SLM)。

标准线性模型的蠕变与应力松弛行为如下图,可见标准线性模型能正确地描述蠕变和应力松弛趋势。其中τ1=η/E1,Ex=E0/(E0+E1)。

SLM用于聚合物黏弹性的近似描述比起二元件模型来说已经有了改善。但是,这些模型仍然只有一个松弛时间,仍然不能完全反映聚合物黏弹性行为。因此,常常采用一般性力学模型即广义Maxwell和广义Kelvin模型来表示。虽然这两类模型是完全等效的,但前者描述应力松弛更为方便,后者描述蠕变较好。下图是广义Maxwell模型。
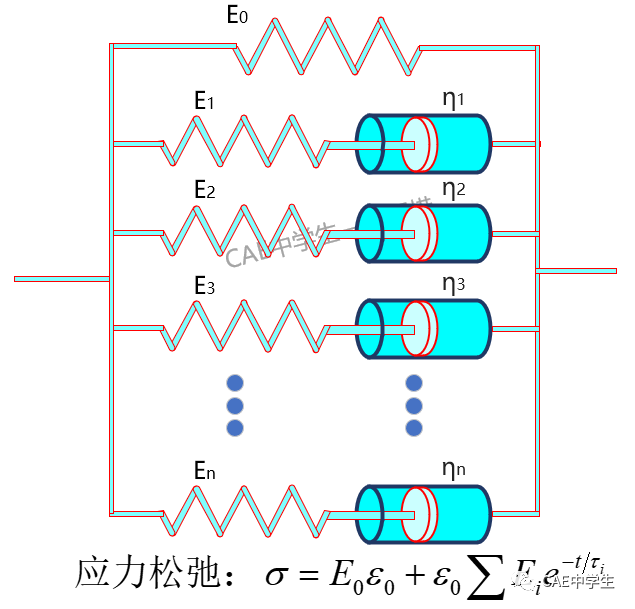
Maxwell模型、Kelvin-Voigt模型、SLM可以看作这个模型的简化模式。
广义麦克斯韦模型也是ANSYS中表示粘弹性的模型,为了在数值上实现Maxwell模型,ANSYS采用应力松弛函数的Prony级数表示法来模拟粘弹性。

4.2.1 粘弹性测试数据
通过曲线拟合描述以Prony级数为函数的粘弹性。
剪切数据与Prony剪切松弛对应,体积数据与Prony体积松弛对应。
4.2.2 粘弹性本构
(1)Prony剪切松弛与体积松弛
Prony级数表示法是用数值方法来表示广义麦克斯韦模型的,是最常用的粘弹性本构,它的松弛公式分为剪切松弛与体积松弛。
Prony剪切松弛本构:

Prony体积松弛本构:
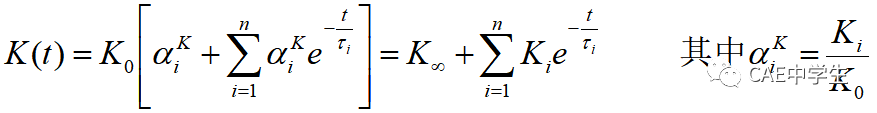
G0、K0表示固相的剪切模量、体积模量,G∞、K∞表示液相的剪切模量、体积模量,n为输入参数个数,t为时间,τi为松弛时间,含义同上文。
(2)William-Landel-Ferry Shift Function
适用于聚合物材料的粘弹性本构,物理描述为:载荷在一固定值以下,尽管发生能量耗损,但变形仍为弹性变形。
(3)Tool-Narayanaswamy Shift Function
适用于玻璃材料的粘弹性本构,与上者不同的是,在温度变化情况下,除了结构松弛,还有明显的体积变化。
可以参考玻璃数据:密度为2390 kg/m, C0=27.4X103 MPa, C∞=0 MPa,体积模量为60.5X 10MPa,1/β =0.53。
(4)Tool-Narayanaswamy W/Fictive Temperature Shift Function
适用于玻璃和刚性聚合物等粘弹性材料的熔化和固化过程,虚拟温度用于描述热循环过程中,应变与时间和温度有更强的相关性
4.2.3 Workbench实例详解
实例1 粘弹性材料曲线拟合,以Prony剪切松弛本构为例。
注意:粘弹性的材料曲线拟合与超弹性本构类似,但是一般需要输入材料的弹性模量与泊松比。建立一个时间——剪切模量数据文档,每个文件对应一个温度,如果有多个温度,必须使用多个文件输入多个温度数据集。推荐使用Excel文件,选择Excel中的数据,复 制到剪切板中。
Step1 准备数据。
下载图惜准备的试验数据(取自于文献【4】),读者也可使用自己试验数据。此处图惜并不想玩什么关注转发领取素材的套路,但还是希望大家能关注点赞转发。

Step2 数据导入。
新建一个Engineering Data,双击左键打开,如图所示。分别点击粘弹性测试数据→剪切数据和粘弹性→Prony剪切松弛,按住左键将两个菜单栏都拖至新建的材料1框处。

在塑性菜单栏中设置材料的弹性模量为100000MPa,泊松比0.25,点击剪切数据—粘弹性1进行编辑,在表格属性菜单栏设置温度为100℃,在时间-剪切模量栏右键粘贴EXCEL中的数据,即可将试验数据导入。

Step2 曲线拟合。
在属性菜单栏中点击Prony剪切松弛,项数即参数个数,默认为1,本例不修改。
曲线拟合——拟合误差默认为归一化误差(标准误差),表示对输入数据不加权,适合一般情况。绝对误差表示对输入数据中大的数据加权,适合大应变情况,本例选择归一化误差。
然后右键点击曲线拟合,在出现的菜单中先点击求解曲线拟合。


再右击曲线拟合——复 制计算值到属性,即可把拟合好的数据赋值给材料参数。


以上便完成了材料曲线的拟合。
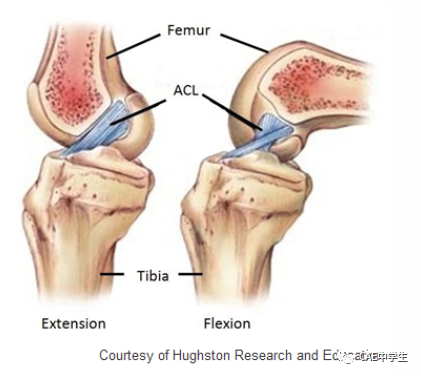
更多Ansys粘弹性工程实例应用,请登录其帮助主页(https://ansyshelp.ansys.com/account/secured?returnurl=/Views/Secured/main_page.html?v=212),参考Mechanical APDL 2022 R2 / Technology Showcase: Example Problems 中的第18例“烤瓷牙的粘弹性分析”与第32例“前交叉韧带ACL模拟”等实例。

写在最后
至此,非线性材料已经完成了弹塑篇、蠕变粘塑篇、超弹篇、粘弹篇的总结,其余本构由于图惜很不熟悉,就不再班门弄斧了。下一篇将解读非线性本构中的一个典型弹塑性材料——垫片,敬请关注。
参考文献:
[1]《Ansys Workbench有限元分析实例详解》——周炬、苏金英
[2]《高分子物理》——华幼卿、金日光
[3]《ANSYS高级结构非线性培训手册》——安世亚太
[4] ANSYS 2022帮助文件
[5] Abaqus帮助文件




