【JY】浅析时程分析中的阻尼设置
(非线性)直接积分法、快速非线性分析(FNA)法等时程分析方法中的阻尼设置尤为重要,以SAP2000为例,进行抛砖引玉,各类软件做法也大同小异,可借鉴与学习。
模态阻尼
模态阻尼是用非耦合的阻尼来模拟结构中的阻尼。每一模态有一个阻尼比 damp,需满足:
模态阻尼有 2 个不同的来源:来自荷载工况的模态阻尼、来自材料的复合模态阻尼,并保证从这些来源的阻尼被加在一起,一般软件都自动确认此和小于 1。
模态工况: 来自荷载工况的模态阻尼1:
来自荷载工况的模态阻尼1: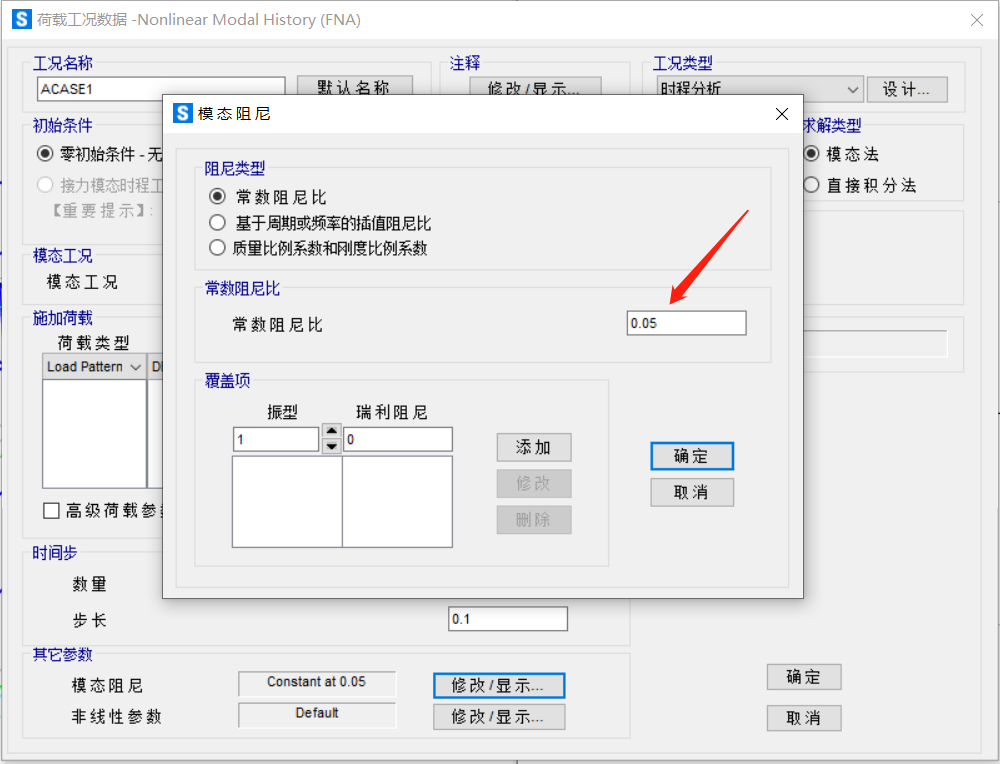 来自荷载工况的模态阻尼2:
来自荷载工况的模态阻尼2: 来自材料的复合模态阻尼:
来自材料的复合模态阻尼:
首先对于非线性分析前,所有通过模态工况得到的模态是必须是恒定的 ,因此对于不同的模态点获得的阻尼比在工况设定中总是确定的。并且在非线性工况上可指定在一系列频率或周期点的阻尼。
模态阻尼构成的阻尼矩阵,是荷载工况得到的模态阻尼叠加材料属性上所获得的模态阻尼进行换算组装,值得注意的是:材料模态阻尼比是为了区分钢-混凝土结构或土-结构等,确定不同材料阻尼比时进行分析,并且若是定义了材料阻尼比,则需要考虑是否取消系统阻尼比,避免重复计算。
FNA法中需要注意的是:
模态阻尼的假定是相对于总刚度矩阵 K 的,其包括了来自非线性单元的有效刚度。此时会影响模态值,从而影响对结构产生的阻尼影响。
如:隔震结构,采用屈服后刚度填写单元有效刚度、则得到的模态点是屈服后周期点,在这些模态点上赋予阻尼比。
理论上最合理的做法是预估本非线性工况下隔震单元的最大变形,并计算得到此时的有效刚度进行填写,得到的模态点进行赋予阻尼比。但事实上,我们在分析前,并无法精确预估隔震单元的最大变形。
建议可采用屈服后刚度填写单元有效刚度,系统阻尼比对结构产生的影响,远小于隔震单元自身的耗能影响。
【JY】基于Ramberg-Osgood本构模型的双线性计算分析
直接积分法需要注意的是:
个人非常不建议在非线性直接积分法计算中采用模态阻尼,除非是为了和FNA进行对比验证!因为在非线性直接积分法中,模态阻尼产生的阻尼矩阵是满秩的:
满秩完全密集的矩阵对于计算速度将带来极大的影响,并且直接积分时程分析中的总自由度数几乎都比所提供的模态数量要大得多,带来的问题就是高频成分缺乏阻尼抑制,极容易带来计算不收敛。通常可以再增加刚度比例阻尼进行抑制,(但如果这样做,不如直接采用瑞利阻尼),通常建议是:
如果模态阻尼影响的最高阶模态频率为𝑓,可以指定频率𝑓的刚度比例阻尼为 0.2%,指定频率10𝑓为 2%,这样给不受模态阻尼衰减的高频提供阻尼。
比例阻尼 (瑞利阻尼)
瑞利阻尼通常用于直接积分法中,其将阻尼矩阵强行解耦,使得矩阵密度和质量矩阵、刚度矩阵在同个量级。这种便捷的方式,使得直接积分法计算速度加快(相对采用模态阻尼的直接积分法)。相关推文可看:
上述文章已经详细阐述,对于瑞利阻尼不过多赘述。比例阻尼的来源依然是材料阻尼、工况定义的系统阻尼,并且模拟直接积分使用的阻尼比值不允许超过 1。
 来自材料的比例阻尼:
来自材料的比例阻尼: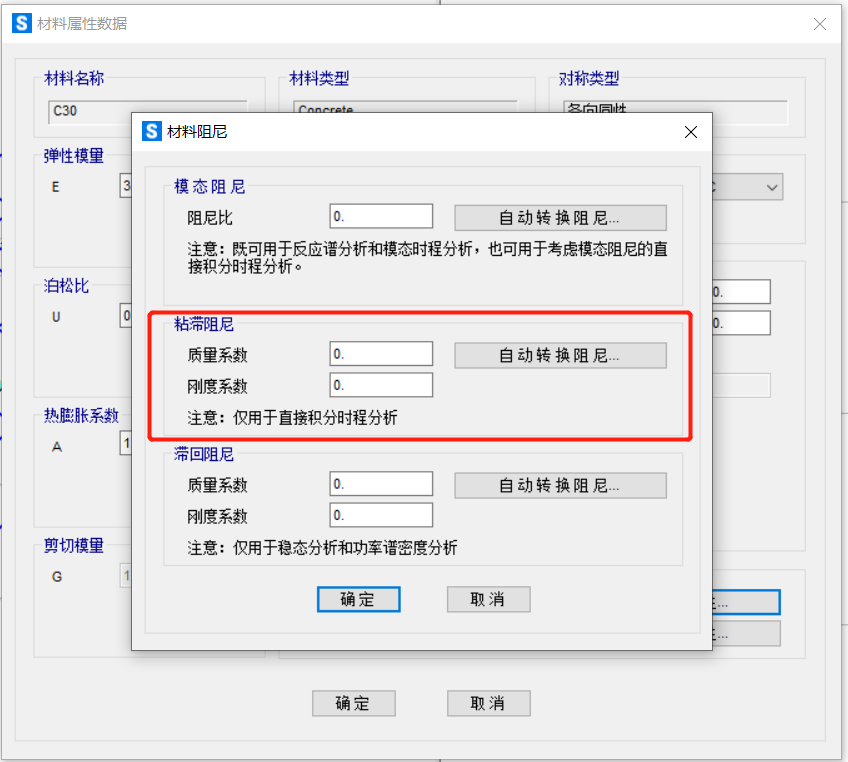 来自荷载工况的比例阻尼:
来自荷载工况的比例阻尼:




