RationalDMIS编程之元素定义
所有元素在测量前,都必须先有理论值,这个理论值或从图纸上获得,或直接从CAD模型中拾取。
作为测量程序,所有的元素在使用前,都必须先有理论值。
在进行各项元素的检测前,都必须先有理论定义:
1、定义点的DMIS格式为:
F(LABEL) = FEAT/POINT, VAR_1, I,J,K
VAR_1为Cart,x,y,z或者POL,r,a,h
那么如果我需要定义一个坐标值为10,20,30,方向为Z轴正方向的点定义语句为:
F(PT1) = FEAT/POINT, CART,10, 20, 30, 0, 0, 1
运行上面的这行语句后,即会出现一个坐标值为10,20,30,方向为0,0,1的点。
2、定义直线元素:
F(LABEL) = FEAT/ LINE,var_1,ni,nj,nk
VAR_1为 UNBND,var_2或者 BND,var_3
VAR_2为 CART,x,y,z,i,j,k或者 POL,r,a,h,i,j,k
VAR_3为 CART,e1x,e1y,e1z,e2x,e2y,e2z或者 POL,e1r,e1a,e1h,e2r,e2a,e2h
上面的部分参数意义:
UNBND:为一条未限制边界的直线(无限长)
BND:为一条限制范围的直线(定长)
e1x,e1y,e1z:
e2x,e2y,e2z:为限制直线的两个端点的直角坐标值
e1r,e1a,e1h:
e2r,e2a,e2h:为限制直线的两个端点的极坐标值
i,j,k:为沿直线方向第一点到第二点的向量
ni,nj,nk:为直线所在平面的向量,可以用来做探头补偿
如语句:
F(LINE1) = FEAT/LINE, BND, CART, -10, -10, -10, 10, 10, 10, -1, 1, 0
所定义的直线LINE1的两个端点坐标为 (-10,-10,-10) (10,10,10) 所在平面的方
向为-1,1,0
3、定义球元素
F(LABEL) = FEAT/SPHERE,var_1,var_2,diam var_3
Var_1为 INNER或者 OUTER
Var_2为 CART,x,y,z或者 POL,r,a,h
Var_3为 i,j,k var_8或者不存在
Var_8为 angle或者不存在
上面部分参数意义:
INNER:为一个内球
OUTER:为一个外球
i,j,k:为球的法向量(如下面图示)
angle:为指示球的可测范围(如下面图示)的角度

4.定义平面元素
F(label)=FEAT/PLANE,var_1,i,j,k
Var_1为 Cart,x,y,z或者 Pol,r,a,h
上面部分参数的意义: x,y,z 为平面上某一点的坐标
5.定义曲线元素
F(label)=FEAT/GCURVE,var_1
Var_1为 CART,x,y,z,i,j,k或者POL,r,a,h,i,j,k
CART,x,y,z,i,j,k,PTDATA,xd,yd,zd,id,jd,kd var_7
POL,r,a,h,i,j,k,PTDATA,rd,ad,hd,id,jd,kd var_8
Var_7为 xd,yd,zd,id,jd,kd var_7或者 xd,yd,zd,id,jd,kd
Var_8为 rd,ad,hd,id,jd,kd var_8或者 rd,ad,hd,id,jd,kd
上面部分参数的意义
x,y,z 曲线所在平面上任意一点的坐标
i,j,k 曲线所在平面的向量.
PTDATA 表示为曲线上每个点的数据(由测量曲线时的实测点来确定)
xd,yd,zd,id,jd,kd 曲线上每一个测量点的坐标和法向
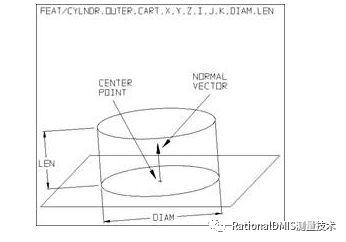
6.定义理论圆柱
F(label)=FEAT/CYLNDR,var_1,var_2,i,j,k,diam var_3
Var_1为 INNER或者OUTER
Var_2为 CART,x,y,z或者 POL,r,a,h
Var_3为 len或者不存在
上面部分参数的意义啊
x,y,z 圆柱为没有边界时,为轴上任意一点的坐标.
圆柱有边界时,为圆柱轴线中点的坐标
i,j,k 为圆柱轴线方向
7.定义理论椭圆
F(label)=FEAT/ELLIPS,var_1,var_2,var_3,i,j,k,diam
Var_1为 INNER或者OUTER
Var_2为 CART,f1x,f1y,f1z,f2x,f2y,f2z或者 POL,f1r,f1a,f1h,f2r,f2a,f2 h
Var_3为 MAJOR或者MINO R
部分参数的意义
f1x,f1y,f1z
f2x,f2y,f2z为椭圆的两个焦点的直角坐标
f1r,f1a,f1h
f2r,f2a,f2h为椭圆的两个焦点的极坐标
MAJOR 表示下面定义的为椭圆的大直径
MINOR 表示下面定义的为椭圆的小直径
椭圆在DMIS标准里是两点定义,为椭圆上任意一点,到两个焦点的距离之和为定值,这样来进行椭圆二次曲线的几何定义.
在RationalDMIS中,元素定义窗口是用椭圆的圆心点坐标,长短轴长度,长轴方向来唯一确定一个椭圆.
8.定义理论圆锥
F(label)=FEAT/CONE,var_1,var_2,i,j,k,ang
Var_1为 INNER或者 OUTER
Var_2为 CART,x,y,z或者 POL,r,a,h
部分参数的意义
CART,x,y,z 为圆锥顶点直角坐标
POL,r,a,h 为圆锥顶点极坐标
i,j,k 为圆锥轴线方向,方向如图示
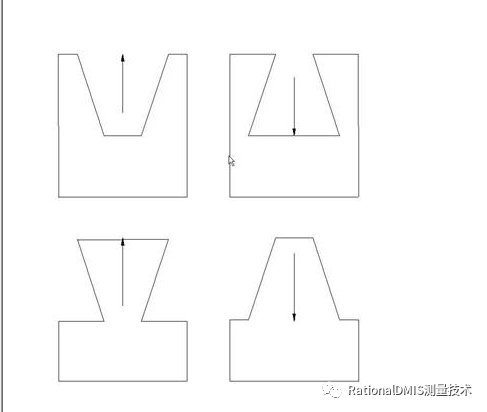
9.定义圆弧
圆弧有两种定义方式:四点定义和角度定义
四点定义格式:
F(label)=FEAT/ARC,4POINT,var_1,e1x,e1y,e1z,mx,my,mz,e2x,e2y,e2z,cx,cy,cz
Var_1 为INNER或者OUTER
e1x,e1y,e1z 为圆弧第一个边缘点的坐标值
mx,my,mz 为圆弧中点的坐标值
e2x,e2y,e2z 为圆弧第二个边缘点的坐标值
cx,cy,cz 为圆弧圆心的坐标
角度定义格式:
F(label)=FEAT/ARC,var_1,var_2,i,j,k,rad,ang1,ang2 var_3
Var_1 为INNER或者OUTER
Var_2 为CART,x,y,z或者POL,r,a,h
Var_3 为is,js,ks或者不存在
部分参数意义
i,j,k 为圆弧所在平面的向量
rad 为一个正整数表示圆弧的半径
ang1 为由Var_3参数确定的主轴所确定的角度
ang2 为对于角度1包含圆弧的角度
is,js,ks 为圆弧起始点在平面上的向量
对于测量时特征元素算法选择:
定义圆、圆弧、平面的拟合算法为最小二乘法,其中圆的算法可以根据程序进行选择,有4种算法可供选择:

最小外接圆:(最小覆盖圆)将所有的测量点都包含在圆内,直径最小的那个圆。
最大内接圆:(最大空圆)所有测量点都在圆外,直径最大的那个圆。
最小区域圆:(最小半径)从这个圆的圆心出发,画两个同心圆,将所有测量点都包含在这
两个同心圆内,在所有符合上面条件的同心圆中,径向距离最小的那一组。
最小二乘圆:(最小平方差)所有测量点到该圆的距离平方和最小。
实际中应用最多的是最小平方差,给出的为参数的平均值,计算方便,同时个别点的偏差对测量结果影响不大。
在配合中,为了顺利进入装配,轴的尺寸应采用最小覆盖圆,而最小半径,主要用于形状
差的评定。




