Wolfram 分析 | 数字13的13种理解
Wolfram 是一个研究数学和科学的公司,我们不惧怕两位数的整数,尤其那个在12和14之间的数字。也就是说,我们没有恐十三数症,不惧怕十三号的周五,也不惧怕任何其他日子。

对于数字 13,除了可以介绍它是三进制下的重复数 1113 以及它是 Prime[6] 的结果外,还有很多可以说道的地方。比如它是三个仅有的威尔逊质数之一,判断方法是  = 2 834 329,它是整数,且还是第五个梅森素数:
= 2 834 329,它是整数,且还是第五个梅森素数:

但是数字 13 除了是质数外,还有很多有意思的内容,以下给出 13 个理由并解释为什么。
首先,13 是很多线性递归的一部分。比如,13是一个斐波那契数,其值之间的比极限为黄金比例,phi, Φ2 = Φ + 1:


这样 Ammann 椅密铺平面的第五个代入(substitution)有 13 把椅子:
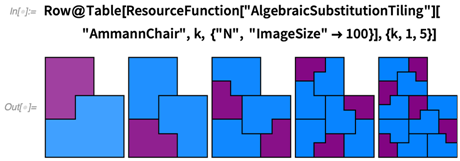
13 还是一个泰波那契数,是 Mark Feinberg 在 14 岁时提出的名词。该数列中项与项之间的比例变为泰波那契常数,t3 = t2 + t + 1:

可以将泰波那契数想象成是没有000的二进制数列:

13 也是 Narayana 的奶牛数,基于 psi 有 Ψ3 = Ψ2 + 1,即超级黄金比例:

这样在 psi 四边密铺(psi-quad tiling)的第六个代入就有 13 个四边形:

阿基米德固体有 13 个,其中黄金比例和泰波那契常数是最显著的特征。同样,阿基米德对偶多面体也有 13 个,都是公平骰 子的形状:
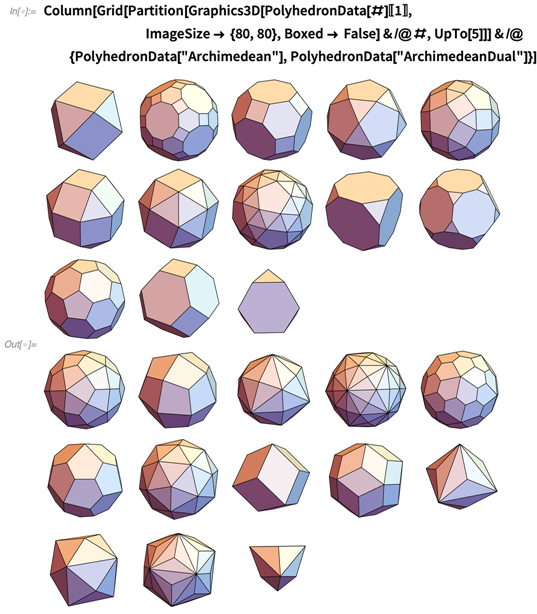
13 可写成 n2 + (n + 1)2 的形式,是一个中心平方数:

三个按钮的密码组合锁有 13 种组合方法,条件是每个按钮只按一次,也让 13 成为了第三个 Fubini 数,也称作有序 Bell 数:

平衡三进制允许三个重量和一个两盘的天平来计量 1 到 13 的重量:

13 的余数图有如下格式。想要使用改图,首先挑一个数字,比如 2,522。然后从 0 开始,遵循 2蓝、1红、5蓝、1红、2蓝、1红、2蓝的规律求得 2,522 除以 13 的余数。这个方法可以用于任意正整数:
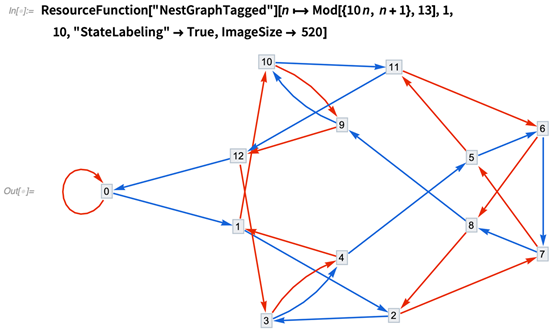
使用 N、E、NE 或 (1,0), (0,1), (1,1) 这样的步长,从点(0,0)到(2,2)可有 13 种走法,是一个称为中心 Delannoy 数的部分合并序列:

可以用 Legendre 多项式来计算这些值:

欧几里得的著作《The Elements》中有 13 本书。如,卷一,论点一讨论了如何形成等边三角形:

长度为 n 的稀疏尺允许要测量的所有整数之间的距离在 n 之内,并用最小数量的记号进行测量。长度为 211 的稀疏尺使用 26 个记号,有 13 个间距为 13 的间隔:

字符串“THIRTEEN”的生物序列如下:

像 An Elementary Introduction to the Wolfram Language 这样的书籍会使用 ISBN-13书号:

最后,在 26 字母的字母系统中,模糊文本的标准是 ROT13 凯撒密码,将每个字母向前回转 13 位:

我们可以用一段代码的模糊文本结束本篇文章:





