干货 | 壁面沸腾模型知识小结

过冷沸腾是指当壁面温度足够导致壁面发生沸腾时，主流区域的液相平均温度仍低于饱和温度的一种物理现象。在这种情况下，壁面传递到液相的能量有一部分被用于继续加热液相，另一部分被用于产生蒸汽相。当蒸汽相脱离壁面进入到主流区域后，其携带的热量也会导致液相温度升高，同时蒸汽相发生冷凝。该现象的传热传质机理就是RPI（Rensselaer Polytechnic Institute）模型的基础。

采用Kurual及Podowski开发的RPI模型，可以模拟壁面沸腾现象中的核态沸腾，而采用Lavieville开发的扩展模型，可以模拟壁面沸腾的偏离泡核沸腾（DNB）。本文对壁面沸腾模型进行简单介绍。

1、基本RPI模型

基本的RPI模型将壁面热流分成三个部分，即液相对流热流、淬灭热流和蒸发热流，方程描述如下：

在发生壁面沸腾时，加热面的表面分为两部分，一部分被核态汽泡覆盖（Ab），另一部分被液相流体覆盖（1-Ab）。因此，液相对流的热流可以表示成：

式中，表示液相的对流换热系数，和分别为壁面温度和液相温度。

淬灭热流表征的汽泡脱离壁面时液相补充到汽泡位置所带走的热量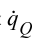，表达式如下：

式中，为导热系数，lamdal为扩散系数。

蒸发热流与汽泡脱离直径、汽泡成核密度、密度、蒸发潜热以及汽泡脱离频率 有关：

 式中，为汽泡体积，基于汽泡脱离直径计算；是汽泡成核密度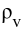，是汽相密度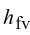，为汽化潜热，f为汽泡脱离频率。

2、方程的封闭

在如上RPI基本模型中，需要采用适当的模型保证方程组封闭。

（1）汽泡面积

汽泡面积的定义是基于汽泡脱离直径和汽泡成核密度，表达式如下：

为了避免超过成核密度经验关系式的适用范围，汽泡面积需要进行限定：

式中，经验常数K通常设置为4，但是该值并不是通用的，可能会在1.8-5之间变化。Del Valle和Kenning提出了经验常数K的计算公式：

式中过冷度雅克比数的定义如下：

（2）汽泡脱离频率

RPI模型的汽泡脱离频率计算公式如下：

（3）汽泡成核密度

汽泡成核密度一般认为与壁面的过热度有关，常用的表达式如下：

根据Lemmert和Chawla的研究，经验参数n和C的取值为n=1.805，C=210。Kocamustafaogullari和Ishii提出了成核密度的另外一种表达式：

 密度函数的定义如下：

（4）汽泡脱离直径

汽泡脱离直径（单位：mm）的经验关系式如下：

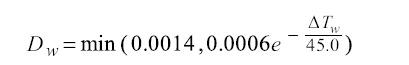
Kocamustafaogullari和Ishii提出的表达式如下：

式中，为壁面接触角。

Unal关系式如下：

式中，P为压力，为近壁面主流速度，=0.61m/s。下表s、l、g分别表示固体、液相和汽相。

当采用RPI模型时，汽相的温度不参与计算，而是固定在饱和温度。在计算过冷沸腾时，该处理方式对结果不会有太大影响，但是在计算偏离泡核沸腾或者临界热流密度、烧干状态时，就有必要考虑到汽相温度的计算了。在这种情况下，壁面热流被分成如下几个部分：

其中，、、分别为液相对流、淬灭、蒸发的热流，为蒸汽相的对流换热热流，为其他可能存在的不凝气体相的对流换热热流。

RPI模型是目前模拟壁面沸腾现象的常用模型，尤其在过冷沸腾的模拟中得到非常广泛的应用，并在此基础上产生了新的模型用于偏离泡核沸腾或临界热流密度的模拟。在使用RPI模型时，重点需要关注汽泡脱离频率、脱离直径、成核密度等的计算。为了更加准确地计算汽液两相流的相间作用力，还需要进一步考虑汽泡直径的分布，例如采用群体平衡模型（PBM）描述汽泡的聚并、破碎等过程。

总的来说，模拟沸腾相变并不容易，现有的模型中或多或少都有着适用范围的限制，在进行数值模拟的过程中，需要根据试验数据和现象，对模型进行不断地修正，方才能够获得较理想的结果。