基于火焰面生成流形方法介绍
湍流燃烧在自然界和工程领域随处可见,湍流燃烧的准确模拟有助于燃烧物理本质的阐释和实现工程应用的高效率和低成本。
燃烧是个复杂的物理、化学过程,从化学方面讲,涉及到众多组分与基元反应,从而构成一个维度很大的状态空间,求解这个状态空间的时间和空间分布对计算资源是个严峻挑战,而且众多组分的求解通常会涉及到大型刚性微分方程组,求解困难。因而需要简化模型来降低状态空间的维数与方程组的刚性。
FGM(Flamelet Generated Manifolds)模型是基于化学反应机理简化和火焰面方法两者的结合。其认为实际燃烧中的高维火焰可以视为一系列低维小火焰的系综,即实际的高维火焰燃烧过程在燃烧化学反应组分空间中的反应流形路径同低维小火焰中类似。FGM方法既可用于预混火焰面,也可用于非预混火焰面,还可利用零维预混气的点火过程来构造简化状态空间。
在FGM方法中,通过计算低维火焰面中生成的反应流形来模拟高维化学反应系统中的反应流形。对于燃烧反应中的低温段和高温段区域,该模型均使用火焰面方程求解,替代了高温区域的低维反应流形求解,可以减少化学反应建表所需的计算量。
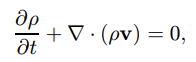
其中,ρ为密度,v是流动速度。
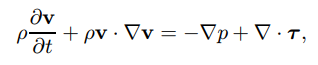
其中,p表示压力,τ粘性应力张量。

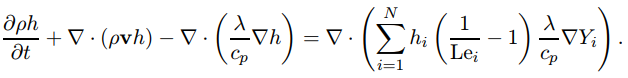
其中,λ为导热系数,刘易斯数:
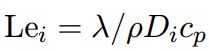
cp为定压比热,Di是第i种组分的扩散系数。化学反应源项由生成项ω+和消耗项ω-构成。
压力p由理想气体状态方程给定:
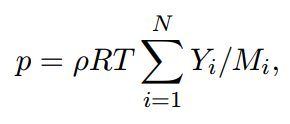
其中,R为通用气体常数,T是温度。
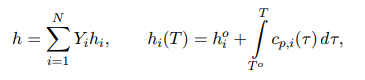
其中,Mi ,cp,i,hi和hi0分别表示第i种组分的摩尔质量,定压比热,比焓和生成焓。
上述方程涉及大量组分,通过化学反应源项强烈耦合,导致方程组刚性很强。需要通过简化化学反应机理来解决这个问题。为此假定在反应中的大多数次要组分处于稳定状态,这意味着这些组分的质量分数方程可以忽略化学反应源项的影响,即:
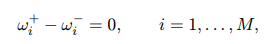
M表示认为是稳态的组分数量。
此方程的解形成了一个流形,可存储在具有N-M维度的数据表中。
根据稳态组分假设,上述方程组的刚性大大降低。
然而,在火焰中有一个重要区域,其化学反应效应和扩散效应是平衡的,需要考虑输运过程的影响来得到更精确的描述。
由于一维火焰中同样存在扩散和对流过程,对其中的化学反应和扩散、对流过程进行组合研究可以引申到更复杂的火焰情况。

图1 预混火焰的示意图,曲线x(s)穿过火焰锋面
如图1所示的预混火焰的一部分,假定一条通过火焰面的曲线x(s),垂直于某组分的质量分数Yi等值面,并将弧长s进行参数化。沿着该曲线的组分质量分数Yi的变化情况可以近似地通过公式03的一维等价形式来描述。
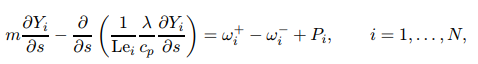
其中,m表示恒定质量流量。
由于x(s)曲线垂直于组分质量分数Yi的等值面,因此一维火焰中的扩散和输运过程可以通过方程08的左边进行表述。火焰拉伸造成的例如质量流量和曲率变化等多维和瞬态效应则在扰动项Pi(s,t)中体现。
在大多数情况下,扰动项Pi和其他项相比很小,因此接下来需要忽略扰动项的影响,建立一组一维微分方程。
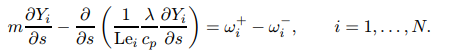
在考虑对流、扩散和化学反应影响下得到的平衡方程09可以认为是稳态的关系。
用同样的方法对能量方程进行处理,最终得到的一组微分方程组,被称为火焰面方程。
如何用火焰面方程组来创建流形?
和ILDM方法类似,区分在反应中守恒的变量(元素的质量分数等)和反应控制的变量(组分的质量分数等)。可以注意到,燃烧混合物的化学成分由守恒变量决定,而从未燃烧到燃烧的过程则由反应控制变量描述,因此也将反应控制变量称为过程变量。
首先,考虑恒定压力p、焓值h和元素质量分数Zj(守恒变量)的情况。选用第i种组分的质量分数Yi作为过程变量来构造用于预混火焰的流形,将方程组09视为自由传播的预混火焰进行求解。这意味着未燃侧的边界条件是Dirichlet型。
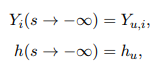
燃烧侧的边界条件则是Neumann型
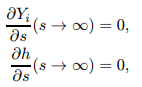
质量流量m是系统的特征值,通过求解方程09得到的曲线Yi(s)由其起始条件(Yu,i, hu,i)确定。
构成空间中的一维流形即表示始于未燃混合物处的火焰面模型。通过这种方式,一维流形连接了构成空间中两个最重要的点:未燃混合物点和反应平衡点。通过增加过程变量的数量,可以提高FGM方法的准确性,尤其当和火焰面方程中其他项相比扰动项Pi不能忽略时。
到目前为止,只考虑了守恒变量p,h和Zj为常数的情况。但这些量中的一个或多个会在空间或时间上发生变化。
例如,在燃烧器中稳定燃烧火焰中,由于辐射可能导致焓降低。为了解释这些焓变化,可以将焓h作为附加控制参数扩展FGM流形维度。针对不同初始焓值hu的火焰面方程09,对d维流形而言,可以获得由d个过程变量和焓h参数化后构成的(d + 1)维流形。类似地可以处理其它守恒变量,得到(d + nc)维流形,其中nc是附加过程控制的数量。附加控制变量nc最大值为ne + 1, ne为元素的数量。对于大多数应用情况而言,只需少量的附加过程变量。
在本文的其余部分将讨论FGM在层流预混燃烧器稳定火焰中的应用。由于在这些火焰中守恒变量仅有焓h发生扰动,因此将采用具有两个控制变量的流形:一个过程变量和焓(d = 1,nc = 1)。
在反应流动代码中实现FGM模型分为两个部分:首先是火焰面结构数据的计算和储存,随后则是FGM模型与多维燃烧计算的耦合。
为了证明FGM方法的性能,采用通过两个控制变量(YO2和h)的生成流形对燃烧器稳定一维火焰进行计算,并将结果与文献[2]中根据完整反应动力学机理获得的结果进行比较。
燃烧器出口位置位于x=0cm处,在x<0cm的燃烧器区域保持Tburner=300K的恒定温度,计算质量流量m从0.005g/cm2s到0.040g/cm2s之间的稳态解。当量混合比下甲烷/空气火焰的绝热质量燃烧速率为m=0.0421g/cm2s,其对应的层流火焰速度为SL=37.5cm/s。
m=0.030g/cm2s时,控制变量YO2和h的变化曲线如图2所示。可以看出FGM模型计算结果和详细化学机理计算得到的结果一致性良好。由于Le数效应引起的大梯度火焰锋面和焓降一起被很好的展现出来。
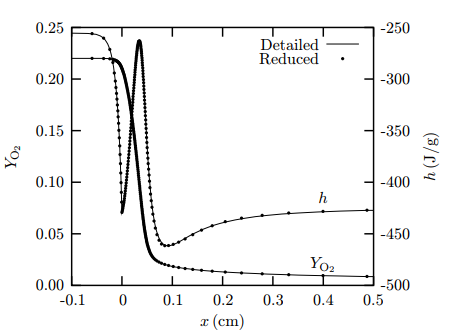
图2 m = 0.030g / cm2s时YO 2与h随x变化曲线
CH2O和H的质量分数随x变化情况如图3所示。
对于这两种IDLM方法很难精确计算的组分而言,FGM模型计算得到的结果同样和详细化学反应机理计算结果吻合的很好。
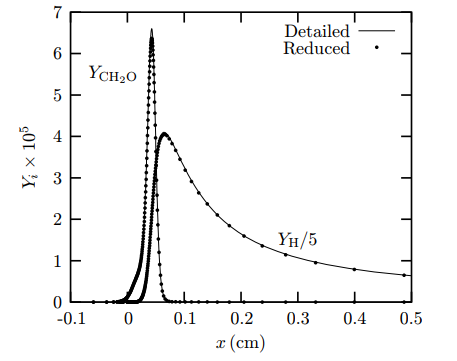
图3 m = 0.030g / cm2s时YCH2O与YH随x变化曲线
图4展示了非绝热燃烧温度和间隙距离与质量流量之间的关系,可以看出在不同质量流量下,FGM模型在非绝热燃烧温度上同详细机理计算结果一致性良好。对于间隙距离,在较低质量流量下两者之间略有差距,但是一致性仍然较好。
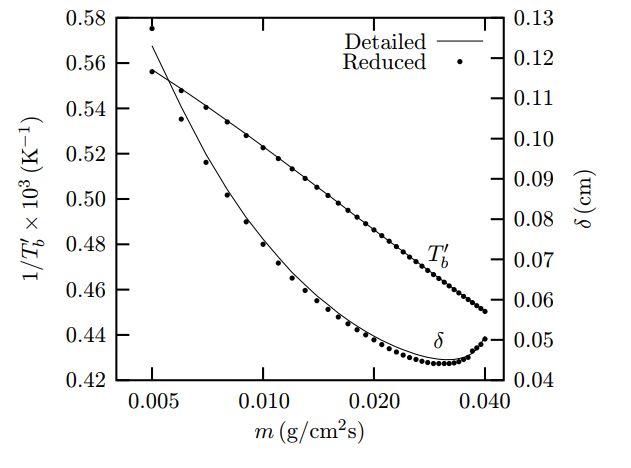
图4 不同入口流量下 Tb’与δ变化曲线
接下来通过计算二维燃烧器中稳定的层流预混火焰来验证FGM模型的精确性。在这个测试案例中,几乎所有在层流预混火焰中发现的特征——如火焰冷却、拉伸和弯曲,都存在。
二维燃烧器的结构如图5所示,燃烧器槽宽6mm,盒宽为24mm。燃烧器和盒子壁面温度维持恒定,Tburner=300K。燃烧器入口处速度分布为抛物线形,最大速度Vmax=1m/s。工质为当量比为0.9的甲烷/空气混合物。
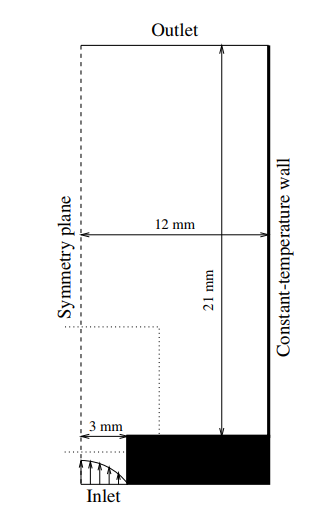
图5 二维燃烧器结构
FGM模型和详细化学反应机理计算得到的温度、CH2O和H的质量分数等值线在部分计算域上的分布如图6所示。可以看出,用FGM模型计算得到的结果和用详细化学反应机理计算得到的结果非常一致。FGM模型不仅能准确捕捉火焰锋面的位置,对组分质量分数的结果同样准确。此外,FGM模型很好地捕捉到了控制燃烧器火焰稳定燃烧的火焰冷却现象。
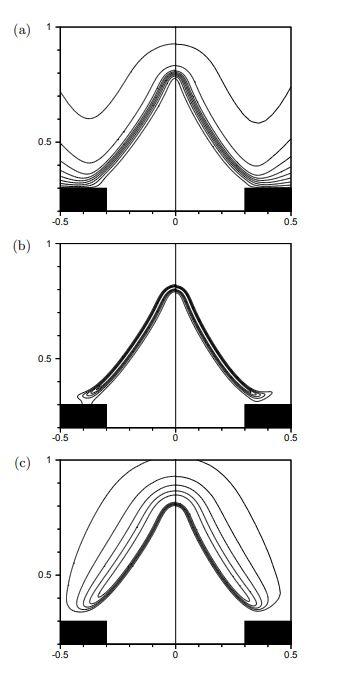
图6 (a)温度 (b)YCH2O (c)YH 等值线
除了准确性之外,高效率是FGM方法的另一个优点。为了给出FGM模型的具体效率提升情况,对FGM模型和详细化学反应机理模型,在相同条件下对1D火焰模拟进行求解,得到计算时间情况如表1所示。
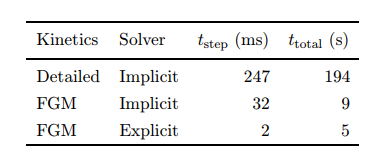
表1 FMG方法和详细化学反应机理计算时间消耗
可以看出,采用FGM模型时,每时间步的CPU计算时间减少约8倍。这种时间上的减少是由要求解的微分方程的数量的减少和化学源项快速评估引起的。FGM模型的另一个优点是可以采用更大的时间步长,因为已经消除了最小的时间尺度的影响。因此,FMG模型的总CPU计算时间比详细化学反应机理模型约少20倍。如果将显式求解器用于FGM模型计算,效率将会提高的更多。
FGM模型能够简化化学反应机理,减少运算资源需求和运算时间消耗,同时计算结果同详细化学反应机理一致性良好,具有应用于燃烧仿真领域的良好前景。
【参考文献】
[1] Oijen J A V, Goey L P H D. Modelling of Premixed LaminarFlames using Flamelet-Generated Manifolds[J]. Combustion Science &Technology, 2000, 161(1):113-137.
[2] Smooke M D. Reduced Kinetic Mechanisms and AsymptoticApproximations for Methane-Air Flames[M]. Springer Berlin Heidelberg, 1991.




